Các Dạng Toán Bài Tích Của Một VecTơ Với Một Số Giải Chi Tiết

Các dạng toán bài Tích của một vectơ với một số giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: CHỨNG MINH ĐẲNG THỨC VECTƠ

Để chứng minh một đẳng thức vectơ, ta thường:

• Chứng minh vế trái bằng vế phải hoặc ngược lại.

• Sử dụng giả thiết suy ra đẳng thức vectơ.

• Dùng các hệ thức như: hệ thức trung điểm, hệ thức trọng tâm tam giác.

• Tính chất của các hình (tam giác đều, tam giác vuông, hình vuông, hình chữ nhật …).

Bài 1. Cho tứ giác $ABCD$. Gọi $M,N$ tương ứng là trung điểm của các cạnh $AB,CD$. Chứng minh rằng $\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} $.

Lời giải

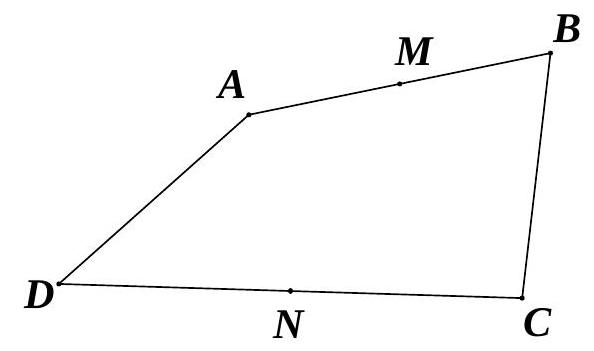
Ta có: $\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} $

$ = 2\overrightarrow {MN} + \left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)$

$ = 2\overrightarrow {MN} + \vec 0 + \vec 0 = 2\overrightarrow {MN} $ (1)

Lại có,$\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {AB} + \overrightarrow {BD} $

$ = \left( {\overrightarrow {BA} + \overrightarrow {AB} } \right) + \overrightarrow {AC} + \overrightarrow {BD} = \vec 0 + \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} $ (2)

Từ (1) và (2) suy ra ĐPCM

Bài 2. Cho tứ giác $ABCD$. Gọi $E,F$ lần lượt là trung điểm của $AB$ và $CD$.

a) Chứng minh rằng: $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {EF} $

b) Gọi $G$ là trung điểm của $EF$. Chứng minh rằng $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0$

Lời giải

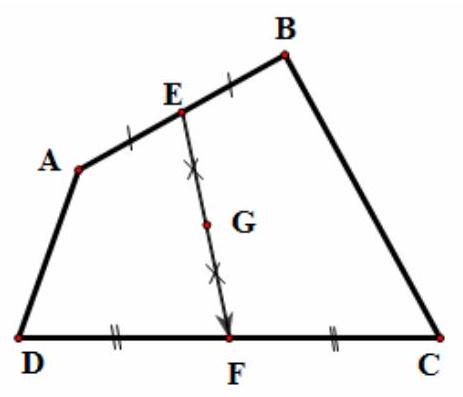
a) $\overrightarrow {AC} + \overrightarrow {BD} = \left( {\overrightarrow {AE}  + \overrightarrow {EF}  + \overrightarrow {FC} } \right) + \left( {\overrightarrow {BE}  + \overrightarrow {EF}  + \overrightarrow {FD} } \right)$

$ = 2\overrightarrow {EF}  + \left( {\overrightarrow {AE}  + \overrightarrow {BE} } \right) + \left( {\overrightarrow {FC}  + \overrightarrow {FD} } \right)$

$ = 2\overrightarrow {EF}  + \vec 0 + \vec 0 = 2\overrightarrow {EF} $ (1)

$\overrightarrow {AD}  + \overrightarrow {BC}  = \left( {\overrightarrow {AE}  + \overrightarrow {EF}  + \overrightarrow {FD} } \right) + \left( {\overrightarrow {BE}  + \overrightarrow {EF}  + \overrightarrow {FC} } \right)$

$ = 2\overrightarrow {EF}  + \vec 0 + \vec 0 = 2\overrightarrow {EF} $ (2)

Từ (1) và (2) suy ra: $\overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {AD}  + \overrightarrow {BC}  = 2\overrightarrow {EF} $

b) $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GE} + 2\overrightarrow {GF} = 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) = 2\vec 0 = \vec 0$

Bài 3. Cho hình bình hành $ABCD$. Chứng minh rằng: $\overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AC} $

Lời giải

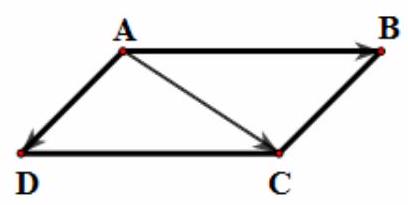
$VT = \overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + 2\overrightarrow {AC} = \overrightarrow {AC} + 2\overrightarrow {AC} = 3\overrightarrow {AC} = VP$

Bài 4. Chứng minh rằng nếu $G$ và $G’$ lần lượt là trọng tâm tam giác $ABC$ và $A’B’C’$ thì $3\overrightarrow {GG’} = \overrightarrow {AA’} + \overrightarrow {BB’} + \overrightarrow {CC’} $.

Lời giải

$VP = \overrightarrow {AA’} + \overrightarrow {BB’} + \overrightarrow {CC’} $

$ = \overrightarrow {AG} + \overrightarrow {G’} + \overrightarrow {G’A’} + \overrightarrow {BG} + \overrightarrow {GG’} + \overrightarrow {G’B’} + \overrightarrow {CG} + \overrightarrow {GG’} + \overrightarrow {G’C’} $

$ = 3\overrightarrow {GG’} + \overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} + \overrightarrow {G’A’} + \overrightarrow {G’B’} + \overrightarrow {G’C’} $

$ = 3\overrightarrow {GG’} – \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \overrightarrow {G’A’} + \overrightarrow {G’B’} + \overrightarrow {G’C’} = 3\overrightarrow {GG’} = VP$.

Bài 5. Cho tam giác $ABC$. Gọi $M,N,P$ lần lượt là trung điểm của $BC,CA,AB$. Chứng minh rằng $\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \vec 0$.

Lời giải

Ta có

$\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right) + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)$

$ = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CA} } \right) + \frac{1}{2}\left( {\overrightarrow {BC} + \overrightarrow {CB} } \right) = \vec 0$

Bài 6. Cho tứ giác $ABCD,O$ là giao điểm của hai đường chéo $AC$ và $BD$. Gọi $G,G’$ theo thứ tự là trọng tâm của tam giác $OAB$ và $OCD$. Chứng minh rằng $\overrightarrow {AC} + \overrightarrow {BD} = 3\overrightarrow {GG’} $.

Lời giải

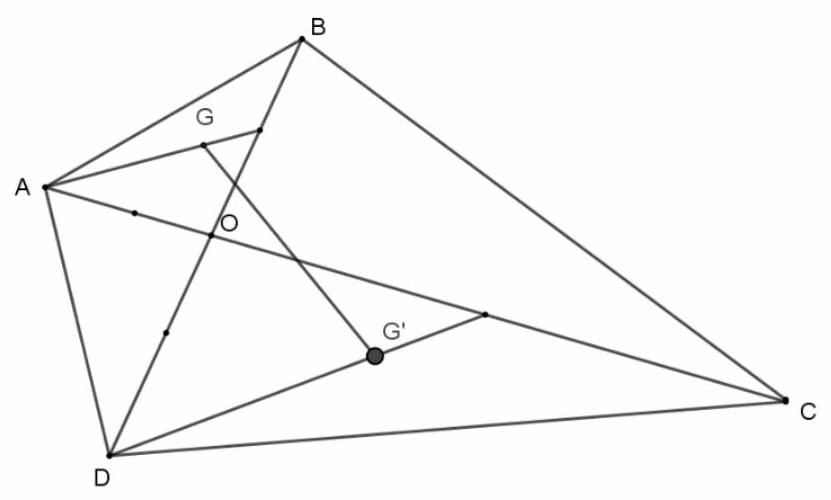
Vì $G’$ là trọng tâm của tam giác $OCD$ nên ta có:

$\overrightarrow {GG’} = \frac{1}{3}\left( {\overrightarrow {GO} + \overrightarrow {GC} + \overrightarrow {GD} } \right)\left( 1 \right)$

Vì $G$ là trọng tâm của tam giác $OAB$ nên ta có:

$\overrightarrow {GO} + \overrightarrow {GA} + \overrightarrow {GB} = \vec 0 \Rightarrow \overrightarrow {GO} = – \left( {\overrightarrow {GA} + \overrightarrow {GB} } \right)\left( 2 \right)$

Từ (1) và $\left( 2 \right) \Rightarrow \overrightarrow {GG’} = \frac{1}{3}\left( {\overrightarrow {GC} – \overrightarrow {GA} + \overrightarrow {GD} – \overrightarrow {GB} } \right) = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$

$ \Rightarrow \overrightarrow {AC} + \overrightarrow {BD} = 3\overrightarrow {GG’} $

Bài 7. Cho tam giác $ABC$ với $H,O,G$ lần lượt là trực tâm, tâm đường tròn ngoại tiếp và trọng tâm của tam giác. Chứng minh $\overrightarrow {OH} = 3\overrightarrow {OG} $.

Lời giải

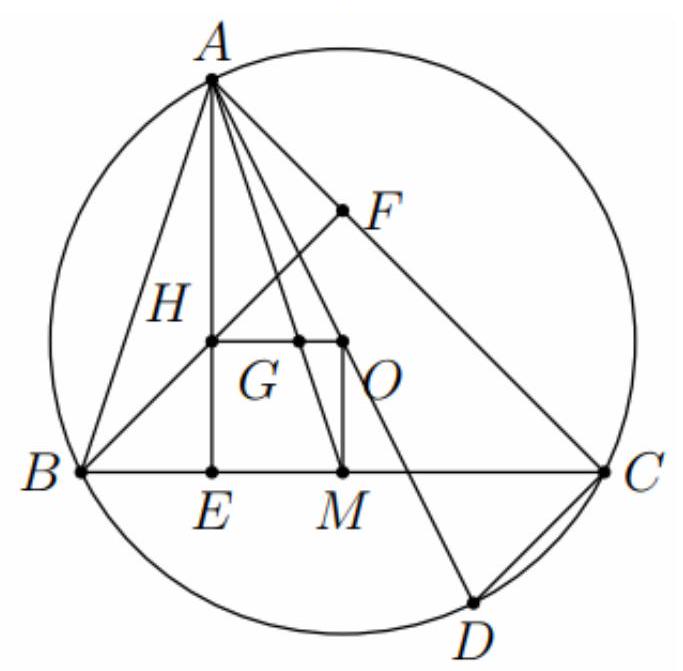
Gọi $D$ là điểm đối xứng của $A$ qua $O$, ta có

$BH//DC$ (cùng vuông góc với $AC$ ) (1) . $CH$ // $BD$ (cùng vuông góc với $AB$ ) (2).

Từ (1) và $\left( 2 \right)$ suy ra tứ giác $BHCD$ là hình bình hành $ \Rightarrow $ ba điểm $H,M,D$ thẳng hàng.

$ \Rightarrow \overrightarrow {AH} = 2\overrightarrow {OM} $.

Ta có $\overrightarrow {OH} = \overrightarrow {OA} + \overrightarrow {AH} = \overrightarrow {OA} + 2\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} $.

Do $G$ là trọng tâm của tam giác $ABC$ nên $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} $. Suy ra $\overrightarrow {OH} = 3\overrightarrow {OG} $.

Bài 8. Cho $\vartriangle ABC$ vuông tại $B$ có $\hat A = {30^ \circ },AB = a$. Gọi $I$ là trung điểm của $AC$. Hãy tính:
a) $\left| {\overrightarrow {BA} + \overrightarrow {BC} } \right|$
b) $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|$

Lời giải

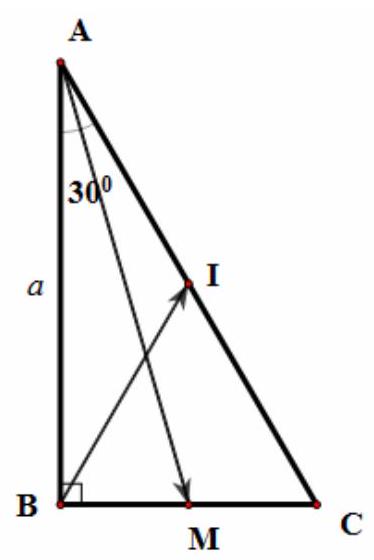
Ta có: $BC = ABtanA = atan{30^ \circ } = \frac{{a\sqrt 3 }}{3},AC = \frac{{AB}}{{cosA}} = \frac{a}{{cos{{30}^ \circ }}} = \frac{{2a\sqrt 3 }}{3}$

a) $\left| {\overrightarrow {BA} + \overrightarrow {BC} \left| = \right|2\overrightarrow {BI} \left| { = 2} \right|\overrightarrow {BI} } \right| = 2BI = 2 \cdot \frac{{AC}}{2} = AC = \frac{{2a\sqrt 3 }}{3}$.

b) $\left| {\overrightarrow {AB} + \overrightarrow {AC} \left| = \right|2\overrightarrow {AM} \left| { = 2} \right|\overrightarrow {AM} } \right| = 2AM = 2\sqrt {A{B^2} + B{M^2}} = 2\sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{6}} \right)}^2}} = \frac{{a\sqrt {39} }}{3}$.

Bài 9. Cho tam giác đều $ABC$ cạnh $a$. Tính
a) $\left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {BC} } \right|$
b) $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|$

Lời giải

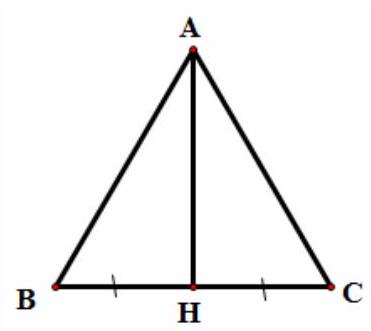
a) $\left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {BC} \left| = \right|\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {AC} \left| = \right|\overrightarrow {AC} + \overrightarrow {AC} \left| = \right|2\overrightarrow {AC} \left| { = 2} \right|\overrightarrow {AC} } \right| = 2AC = 2a$ b) Gọi $H$ là trung điểm của $BC$. Ta có:

$\left| {\overrightarrow {AB} + \overrightarrow {AC} \left| = \right|2\overrightarrow {AH} \left| { = 2} \right|\overrightarrow {AH} } \right| = 2AH = 2\sqrt {A{B^2} – B{H^2}} = 2\sqrt {{a^2} – {{\left( {\frac{a}{2}} \right)}^2}} = a\sqrt 3 $

DẠNG 2: BIỂU THỊ MỘT VECTƠ THEO HAI VECTƠ KHÔNG CÙNG PHƯƠNG

Để phân tích một vectơ theo hai vectơ không cùng phương, ta thường sử dụng:

• Qui tắc ba điểm để phân tích các vectơ.

• Các hệ thức thường dùng như: hệ thức trung điểm, hệ thức trọng tâm tam giác.

• Tính chất của các hình (tam giác đều, tam giác vuông, hình vuông, hình chữ nhật …).

Bài 1. Cho tam giác $ABC$. Gọi $M$ là một điểm trên cạnh $BC$ sao cho $MB = 2MC$. Hãy phân tích vecto $\overrightarrow {AM} $ theo hai vectơ $\overrightarrow {AB} ;\overrightarrow {AC} $.

Lời giải

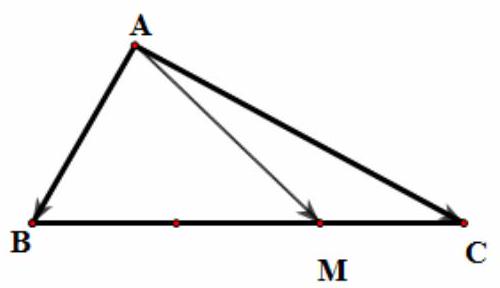
Ta có: $\overrightarrow {AM} = \overrightarrow {AC} + \overrightarrow {CM} = \overrightarrow {AC} – \frac{1}{3}\overrightarrow {BC} = \overrightarrow {AC} – \frac{1}{3}\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} $

$ \Rightarrow \overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} $

Bài 2. Cho $\vartriangle ABC$ có trọng tâm $G$. Cho các điểm $D,E,F$ lần lượt là trung điểm của các cạnh $BC,CA,AB$ và $I$ là giao điểm của $AD$ và $EF$. Đặt $\vec u = \overrightarrow {AE} ,\vec v = \overrightarrow {AF} $. Hãy phân tích các vectơ $\overrightarrow {AI} $, $\overrightarrow {AG} ,\overrightarrow {DE} ,\overrightarrow {DC} $ theo hai vectơ $\vec u$ và $\vec v$.

Lời giải

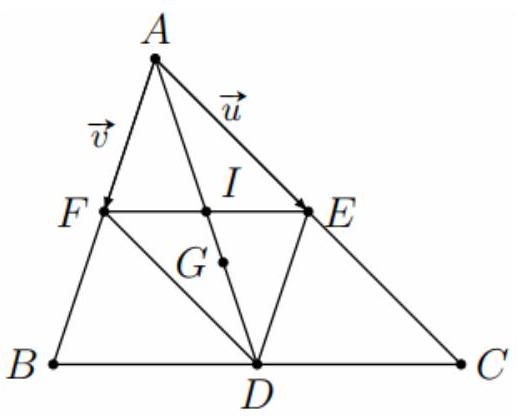
Ta có: $AEDF$ là hình bình hành $ \Rightarrow \overrightarrow {AD} = \overrightarrow {AE} + \overrightarrow {AF} $

Ta có $\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AD} = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {AF} } \right) = \frac{1}{2}\left( {\vec u + \vec v} \right)$

$\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AD} = \frac{2}{3}\left( {\overrightarrow {AE} + \overrightarrow {AF} } \right) = \frac{2}{3}\left( {\vec u + \vec v} \right)$

$\overrightarrow {DE} = \overrightarrow {FA} = – \overrightarrow {AF} = 0 \cdot \vec u + \left( { – 1} \right)\vec v$
$\overrightarrow {DC} = \overrightarrow {FE} = \overrightarrow {AE} – \overrightarrow {AF} = \vec u – \vec v$

Bài 3. Cho $AK$ và $BM$ là hai trung tuyến của tam giác $ABC$, trọng tâm $G$. Hãy phân tích các vectơ $\overrightarrow {AB} ,\overrightarrow {BC} ,\overrightarrow {CA} $ theo hai vectơ $\vec u = \overrightarrow {AK} ,\vec v = \overrightarrow {BM} $

Lời giải

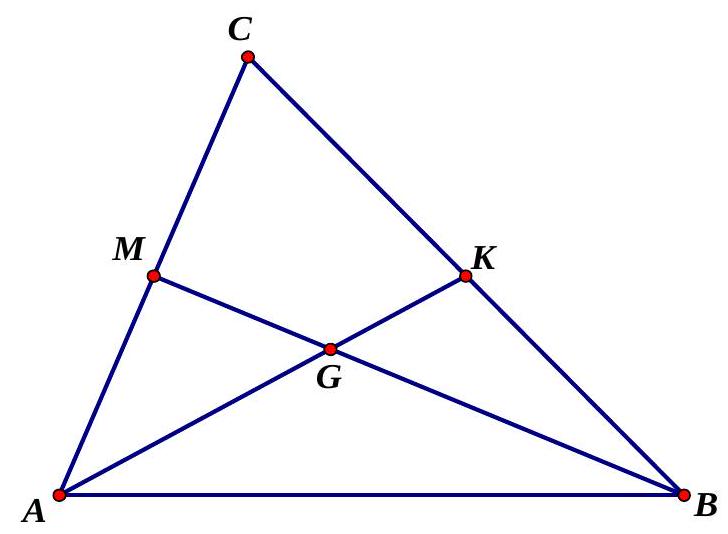
$*\overrightarrow {AB} = \overrightarrow {AG} + \overrightarrow {GB} = \frac{2}{3}\overrightarrow {AK} – \frac{2}{3}\overrightarrow {BM} $

$*\overrightarrow {BC} = 2\overrightarrow {BK} = 2\left( {\overrightarrow {BG} + \overrightarrow {GK} } \right) = 2 \cdot \frac{2}{3}\overrightarrow {BM} + \frac{1}{3}\overrightarrow {AK} = \frac{1}{3}\overrightarrow {AK} + \frac{4}{3}\overrightarrow {BM} $

$*\overrightarrow {CA} = – \overrightarrow {AC} = – \left( {\overrightarrow {AK} + \overrightarrow {KC} } \right) = – \left( {\overrightarrow {AK} + \frac{1}{2}\overrightarrow {BC} } \right)$

Bài 4. Cho tam giác $ABC$. Điểm $M$ nằm trên cạnh $BC$ sao cho $MB = 2MC$. Hãy phân tích vectơ $\overrightarrow {AM} $ theo hai vector $\vec u = \overrightarrow {AB} ,\;\vec v = \overrightarrow {AC} $.

Lời giải

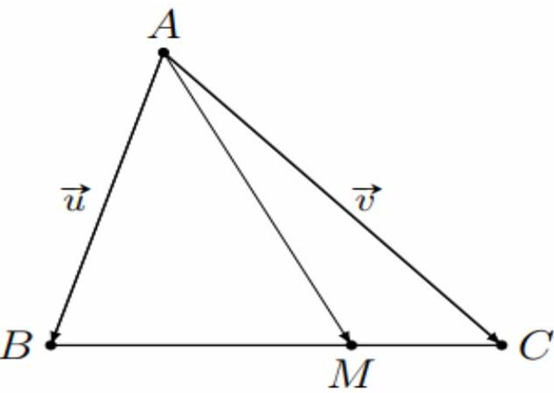
Từ giả thiết $MB = 2MC$ ta dễ dàng chứng minh được $\overrightarrow {BM} = \frac{2}{3}\overrightarrow {BC} $.

Do đó $\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BC} $ mà $\overrightarrow {BC} = \overrightarrow {AC} – \overrightarrow {AB} \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \frac{1}{3}\vec u + \frac{2}{3}\vec v$.

Bài 5. Cho hình bình hành $ABCD$. Gọi $M$ là trung điểm của cạnh $BC$. Hãy biểu thị $\overrightarrow {AM} $ theo hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {AD} $.

Lời giải

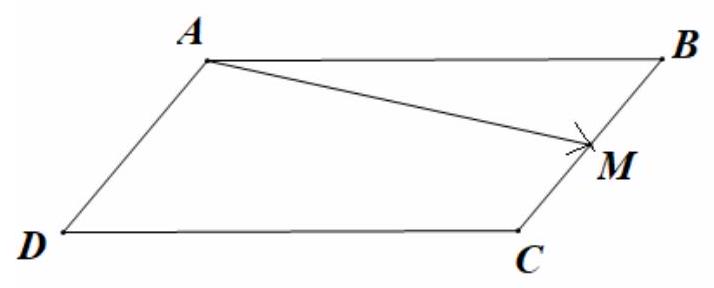
$\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2} \cdot \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AD} $

DẠNG 3: HAI VECTƠ CÙNG PHƯƠNG-BA ĐIỂM THẲNG HÀNG-HAI ĐIỂM TRÙNG NHAU

Để chứng minh ba điểm $A,B,C$ thẳng hàng ta chứng minh ba điểm đó thoả mãn đẳng thức $\overrightarrow {AB} = k\overrightarrow {AC} $, với $k \ne 0$.

• Để chứng minh hai điểm $M,N$ trùng nhau ta chứng minh chúng thoả mãn đẳng thức $\overrightarrow {OM} = \overrightarrow {ON} $, với O là một điểm nào đó hoặc $\overrightarrow {MN} = \vec 0$.

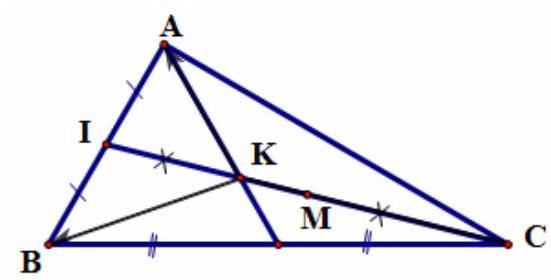
Bài 1. Cho tam giác $ABC$ có trung tuyến $AM$. Gọi $I$ là trung điểm $AM$ và $K$ là điểm thuộc $AC$ sao cho $AK = \frac{1}{3}AC$. Chứng minh ba điểm $B,I,K$ thẳng hàng.

Lời giải

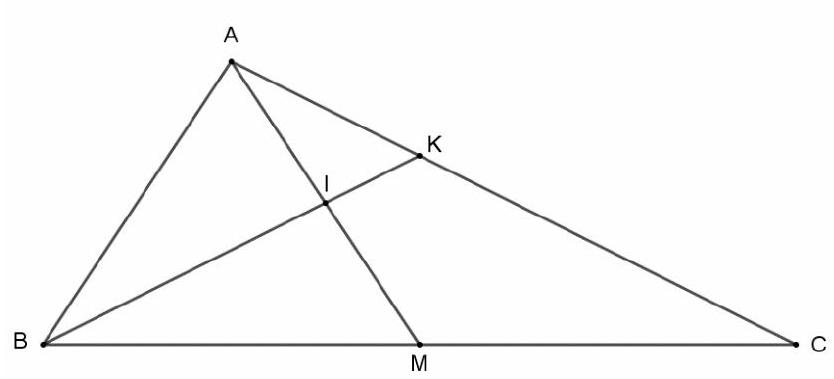
Ta có $I$ là trung điểm của $AM \Rightarrow 2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} $.

Mặt khác $M$ là trung điểm của $BC$ nên $\overrightarrow {BM} = \frac{1}{2}\overrightarrow {BC} $.

Do đó $2\overrightarrow {BI} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {BC} \Leftrightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} $

$\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{3}\overrightarrow {AC} = \overrightarrow {BA} + \frac{1}{3}\left( {\overrightarrow {BC} – \overrightarrow {BA} } \right) = \frac{2}{3}\overrightarrow {BA} + \frac{1}{3}\overrightarrow {BC} $

$ \Leftrightarrow 3\overrightarrow {BK} = 2\overrightarrow {BA} + \overrightarrow {BC} \left( 2 \right)$.

Từ (1) và $\left( 2 \right) \Rightarrow 3\overrightarrow {BK} = 4\overrightarrow {BI} \Rightarrow \overrightarrow {BK} = \frac{4}{3}\overrightarrow {BI} $.

Suy ra 3 điểm $B,I,K$ thẳng hàng.

Bài 2. Cho tam giác $ABC$. Hai điểm $M,N$ được xác định bởi hệ thức: $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0$ và $\overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$. Chứng minh $MN//AC$.

Lời giải

Ta có

$\overrightarrow {BC} + \overrightarrow {MA} + \overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0 \Leftrightarrow \overrightarrow {AC} + \overrightarrow {MN} – 3\overrightarrow {AC} = \vec 0 \Leftrightarrow \overrightarrow {MN} = 2\overrightarrow {AC} \left( 1 \right).$

Mặt khác, $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0 \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AM} $.

Do ba điểm $A,B,C$ không thẳng hàng nên bốn điểm $A,B,C,M$ là bốn đỉnh của hình bình hành $BCMA \Rightarrow $ ba điểm $A,M,C$ không thẳng hàng $\left( 2 \right)$.

Từ (1) và (2) suy ra $MN//AC$.

DẠNG 4: XÁC ĐỊNH ĐIỂM THỎA MÃN ĐẲNG THỨC VECTƠ

Để xác định một điểm $M$ ta cần phải chỉ rõ vị trí của điểm đó đối với hình vẽ. Thông thường ta biến đổi đẳng thức vectơ đã cho về dạng $\overrightarrow {OM} = \vec a$, trong đó $O$ và $\vec a$ đã được xác định. Ta thường sử dụng các tính chất về:

• Điểm chia đoạn thẳng theo tỉ số $k$.

• Hình bình hành.

• Trung điểm của đoạn thẳng.

• Trọng tâm tam giác, …

Bài 1. Cho tam giác $ABC$. Xác định vị trí của điểm $M$ sao cho $\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \vec 0$

Lời giải

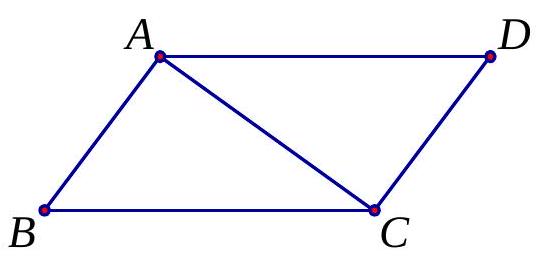
$\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {CM} = \overrightarrow {BA} $.

Vậy $M$ thỏa mãn $CBAM$ là hình bình hành.

Bài 2. Cho tam giác $ABC$ có trọng tâm $G$ và $N$ là điểm thỏa mãn $\overrightarrow {AN} = \overrightarrow {GC} $. Hãy xác định vị trí điểm $N$.

Lời giải

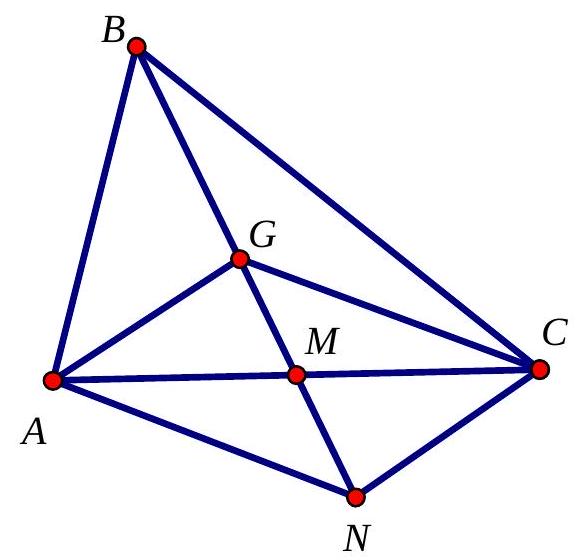
Do $\overrightarrow {AN} = \overrightarrow {GC} $ và $A,C,G$ không thẳng hàng nên $AGCN$ là hình bình hành.

Vậy $N$ đối xứng với $G$ qua trung điểm $M$ của $AC$.

Bài 3. Cho tam giác $ABC$. Gọi $M,P,Q$ lần lượt là trung điểm các cạnh $AB,BC,CA$ và $N$ là điểm thỏa mãn $\overrightarrow {MP} = \overrightarrow {CN} $. Hãy xác định vị trí điểm $N$.

Lời giải

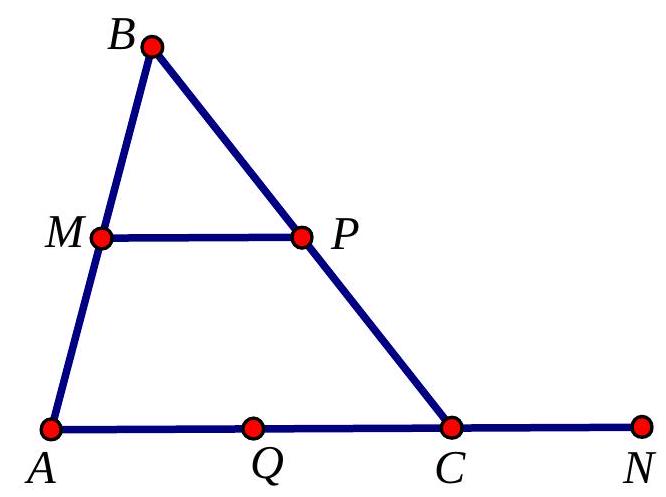
Do $\overrightarrow {MP} = \overrightarrow {CN} $ nên $MP = CN$ và $\overrightarrow {MP} ,\overrightarrow {CN} $ cùng hướng.

Vậy $N$ đối xứng với $Q$ qua $C$.

Bài 4. Cho hình bình hành $ABCD$. Hãy tìm điểm $M$ để $\overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} $. Tìm mối quan hệ giữa hai vec tơ $\overrightarrow {CD} $ và $\overrightarrow {CM} $.

Lời giải

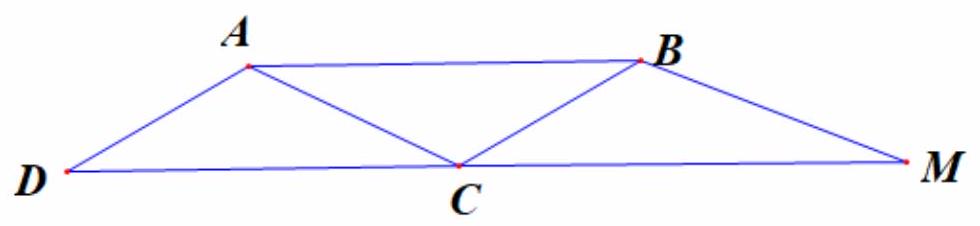
Ta có thep quy tắc hình bình hành $\overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} \Leftrightarrow \overrightarrow {BM} = \overrightarrow {AC} $ nên $M$ là đỉnh thứ tư của hình bình hành BACM ( như hình vẽ).

Bài 5. Cho đoạn thẳng $AB$ và $M$ là một điểm nằm trên đoạn $AB$ sao cho $AM = \frac{1}{5}AB$. Tìm $k$ trong các đẳng thức sau:
a) $\overrightarrow {AM} = k\overrightarrow {AB} $
b) $\overrightarrow {MA} = k\overrightarrow {MB} $
c) $\overrightarrow {MA} = k\overrightarrow {AB} $

Lời giải

a) $\overrightarrow {AM} = k\overrightarrow {AB} \Rightarrow \left| k \right| = \frac{{\left| {\overrightarrow {AM} } \right|}}{{\left| {\overrightarrow {AB} } \right|}} = \frac{{AM}}{{AB}} = \frac{1}{5}$, mà $\overrightarrow {AM} $ cùng hướng $\overrightarrow {AB} \Rightarrow k = \frac{1}{5}$.

b) $\overrightarrow {MA} = k\overrightarrow {MB} \Rightarrow \left| k \right| = \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = \frac{{MA}}{{MB}} = \frac{1}{4}$, mà $\overrightarrow {MA} $ ngược hướng $\overrightarrow {MB} \Rightarrow k = – \frac{1}{4}$.

c) $\overrightarrow {MA} = k\overrightarrow {AB} \Rightarrow \left| k \right| = \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {AB} } \right|}} = \frac{{MA}}{{AB}} = \frac{1}{5}$, mà $\overrightarrow {MA} $ ngược hướng $\overrightarrow {AB} \Rightarrow k = – \frac{1}{5}$.

Bài 6. Cho $\vec a = \overrightarrow {AB} $ và điểm $O$. Xác định hai điểm $M$ và $N$ sao cho: $\overrightarrow {OM} = 3\vec a;\overrightarrow {ON} = – 4\vec a$.

Lời giải

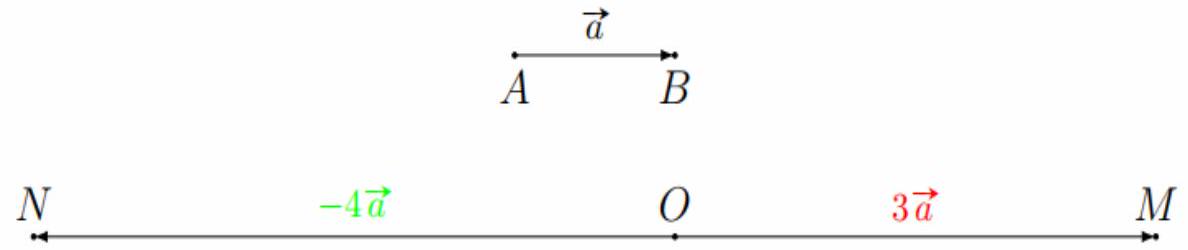
Vẽ $d$ đi qua $O$ và song song với giá của $\vec a$ (nếu $O$ thuộc giá của $\vec a$ thì $d$ là giá của $\vec a$ ).

• Trên $d$ lấy điểm $M$ sao cho $OM = 3\left| {\vec a} \right|,\overrightarrow {OM} $ và $\vec a$ cùng hướng. Khi đó $\overrightarrow {OM} = 3\vec a$.

• Trên $d$ lấy điểm $N$ sao cho $ON = 4\left| {\vec a} \right|,\overrightarrow {ON} $ và $\vec a$ ngược hướng nên $\overrightarrow {ON} = – 4\vec a$.

Bài 7. Cho hai điểm phân biệt $A,B$. Xác định điểm $M$ biết $2\overrightarrow {MA} – 3\overrightarrow {MB} = \vec 0$

Lời giải

Ta có:

$2\overrightarrow {MA} – 3\overrightarrow {MB} = \vec 0 \Leftrightarrow 2\overrightarrow {MA} – 3\left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) = \vec 0 \Leftrightarrow – \overrightarrow {MA} – 3\overrightarrow {AB} = \vec 0 \Leftrightarrow \overrightarrow {AM} = 3\overrightarrow {AB} $

$ \Rightarrow \overrightarrow {AM} ,\overrightarrow {AB} $ cùng hướng và $AM = 3AB$.

Bài 8. Cho tam giác $ABC$.

a) Tìm điểm $K$ sao cho $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {CB} $

b) Tìm điểm $M$ sao cho $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \vec 0$

Lời giải

a) Ta có: $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {CB} \Leftrightarrow \overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {KB} – \overrightarrow {KC} \Leftrightarrow \overrightarrow {KA} + \overrightarrow {KB} + \overrightarrow {KC} = \vec 0$

$ \Rightarrow K$ là trọng tâm của tam giác $ABC$.

b) Gọi $I$ là trung điểm của $AB$.

Ta có: $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \vec 0 \Leftrightarrow 2\overrightarrow {MI} + 2\overrightarrow {MC} = \vec 0 \Leftrightarrow \overrightarrow {MI} + \overrightarrow {MC} = \vec 0$ $ \Rightarrow M$ là trung điểm của $IC$.

Bài 9. Cho hai điểm phân biệt $A$ và $B$.

a) Hãy xác định điểm $K$ sao cho $\overrightarrow {KA} + 2\overrightarrow {KB} = \vec 0$.

b) Chứng minh rằng với mọi điểm $O$, ta có $\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} $.

Lời giải

a) $\overrightarrow {KA} + 2\overrightarrow {KB} = \vec 0 \Leftrightarrow \overrightarrow {KA} + 2\left( {\overrightarrow {KA} + \overrightarrow {AB} } \right) = \vec 0 \Leftrightarrow 3\overrightarrow {KA} = – 2\overrightarrow {AB} \Leftrightarrow \overrightarrow {AK} = \frac{2}{3}\overrightarrow {AB} $

b) Ta có: $\overrightarrow {KA} + 2\overrightarrow {KB} = \vec 0 \Leftrightarrow \overrightarrow {KA} = – 2\overrightarrow {KB} $ $\frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} = \frac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \frac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) = \overrightarrow {OK} + \frac{1}{3}\overrightarrow {KA} + \frac{2}{3}\overrightarrow {KB} = \overrightarrow {OK} + \frac{1}{3}\left( { – 2\overrightarrow {KB} } \right) + \frac{2}{3}\overrightarrow {KB} = \overrightarrow {OK} $

Bài 10. Cho tam giác $ABC$.

a) Hãy xác định điểm $M$ để $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \vec 0$.

b) Chứng minh rằng với mọi điểm $O$, ta có $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} $.

Lời giải

a)

$\begin{array}{*{20}{r}}
{}&{\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \vec 0} \\
{}&{\; \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MA} + \overrightarrow {AB} + 2\overrightarrow {MA} + 2\overrightarrow {AC} = \vec 0} \\
{}&{\; \Leftrightarrow 4\overrightarrow {MA} = – \left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)} \\
{}&{\; \Leftrightarrow \overrightarrow {AM} = \frac{1}{4}\left( {\overrightarrow {AB} + 2\overrightarrow {AC} } \right)}
\end{array}$

b) $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {OM} + \overrightarrow {MB} + 2\overrightarrow {OM} + 2\overrightarrow {MC} = 4\overrightarrow {OM} $

DẠNG 5: TÌM TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VECTƠ

Để tìm tập hợp điểm $M$ thoả mãn một đẳng thức vectơ ta biến đổi đẳng thức vectơ đó để đưa về các tập hợp điểm cơ bản đã biết.

• Nếu $\left| {\overrightarrow {MA} \left| = \right|\overrightarrow {MB} } \right|$ với $A,B$ cố định cho trước thì $M$ nằm trên đường trung trực của $AB$.

• Nếu $|\overrightarrow {MA} \left| { = k} \right\rangle 0$ với $A$ cố định cho trước thì $M$ nằm trên đường tròn tâm $A$ bán kính $R = k$.

• Nếu $\overrightarrow {MA} = k\left| {\overrightarrow {AB} } \right|$ với $A,B$ cố định cho trước thì $M$ nằm trên đường tròn tâm $A$, bán kính $R = k \cdot AB,k \in \mathbb{R}$.

• Nếu $\overrightarrow {MA} = k\overrightarrow {AB} $ với $A,B$ cố định, $k$ là số thực thay đổi thì tập hợp điểm $M$ là đường thẳng $AB$.

• Nếu $\overrightarrow {MA} = k\overrightarrow {BC} $ với $A,B,C$ cố định, $k$ là số thực thay đổi thì tập hợp điểm $M$ là đường thẳng qua $A$ và song song với $BC$.

• Nếu $\left| {\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|\overrightarrow {MC} + \overrightarrow {MD} } \right|$ với $A,B,C,D$ cố định cho trước thì tập hợp điểm $M$ nằm trên đường trung trực của $IJ$ với $I,J$ lần lượt là trung điểm của $AB$ và $CD$.

Bài 1. Cho 2 điểm cố định $A,B$. Tìm tập hợp các điểm $M$ sao cho:
a) $\left| {\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|\overrightarrow {MA} – \overrightarrow {MB} } \right|$
b) $\left| {2\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|\overrightarrow {MA} + 2\overrightarrow {MB} } \right|$.

Bài 2. Cho $\vartriangle ABC$. Tìm tập hợp các điểm $M$ thỏa điều kiện :
a) $\overrightarrow {MA} = \overrightarrow {MB} $
b) $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \vec 0$
c) $\left| {\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|\overrightarrow {MA} – \overrightarrow {MB} } \right|$
d) $\left| {\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|\overrightarrow {MA} \left| + \right|\overrightarrow {MB} } \right|$
e) $\left| {\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|\overrightarrow {MA} + \overrightarrow {MC} } \right|$

Bài 3. Cho $\vartriangle ABC$. Tìm tập hợp các điểm $M$ sao cho:
a) $\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \left| { = \frac{3}{2}} \right|\overrightarrow {MB} + \overrightarrow {MC} } \right|$
b) $\left| {\overrightarrow {MA} + \overrightarrow {BC} \left| = \right|\overrightarrow {MA} – \overrightarrow {MB} } \right|$
c) $\left| {2\overrightarrow {MA} + \overrightarrow {MB} \left| = \right|4\overrightarrow {MB} – \overrightarrow {MC} } \right|$
d) $\left| {4\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \left| = \right|2\overrightarrow {MA} – \overrightarrow {MB} – \overrightarrow {MC} } \right|$.

Bài 4. Cho $\vartriangle ABC$.
a) Xác định điểm I sao cho: $3\overrightarrow {IA} – 2\overrightarrow {IB} + \overrightarrow {IC} = \vec 0$.
b) Tìm tập hợp các điểm $H$ sao cho: $\left| {3\overrightarrow {HA} – 2\overrightarrow {HB} + \overrightarrow {HC} \left| = \right|\overrightarrow {HA} – \overrightarrow {HB} } \right|$.
c) Tìm tập hợp các điểm $K$ sao cho: $2\left| {\overrightarrow {KA} + \overrightarrow {KB} + \overrightarrow {KC} \left| { = 3} \right|\overrightarrow {KB} + \overrightarrow {KC} } \right|$