Đề Thi Giữa Học Kỳ 2 Toán 11 Cánh Diều Giải Chi Tiết-Đề 1

Đề thi giữa học kỳ 2 Toán 11 Cánh diều giải chi tiết-Đề 1 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mối câu hỏi thi sinh chỉ chọn một phuơng án.

Câu 1: Khi gieo một đồng tiền (có hai mặt $S,N$ ) cân đối và đồng chất hai lần. Không gian mẫu của phép thử là:

A. $\left\{ {SS,NN,SN} \right\}$.

B. $\left\{ {SS,NN,NS} \right\}$.

C. $\left\{ {SS,NN,SN,NS} \right\}$.

D. $\left\{ {S,N} \right\}$.

Câu 2: Cho $A$ và $\overline A $ là hai biến cố đối nhau. Khẳng định nào sau đây đúng?

A. $P\left( A \right) + P\left( {\overline A } \right) = 0$.

B. $P\left( A \right) = – 1 + P\left( {\overline A } \right)$.

C. $P\left( A \right) = P\left( {\overline A } \right)$.

D. $P\left( A \right) = 1 – P\left( {\overline A } \right)$.

Câu 3: Cho hình chóp $S.ABC$ có $SA$ vuông với đáy. Xác định góc giữa $SC$ và $\left( {ABC} \right)$.

A. $\widehat {SAC}$.

B. $\widehat {SCA}$.

C. $\widehat {ASC}$.

D. $\widehat {SCB}$.

Câu 4: Khẳng định nào sau đây sai?

A. Nếu đường thẳng $\left( d \right)$ vuông góc với hai đường thẳng nằm trong $\left( \alpha \right)$ thì $d \bot \left( \alpha \right)$.

B. Nếu đường thẳng $d \bot \left( \alpha \right)$ thì $\left( d \right)$ vuông góc với mọi đường thẳng trong $\left( \alpha \right)$.

C. Nếu đường thẳng $\left( d \right)$ vuông góc với hai đường thẳng cắt nhau nằm trong $\left( \alpha \right)$ thì $\left( d \right)$ vuông góc với bất kì đường thẳng nào nằm trong $\left( \alpha \right)$.

D. Nếu $d \bot \left( \alpha \right)$ và đường thẳng $a//\left( \alpha \right)$ thì $d \bot a$.

Câu 5: Cho hình lăng trụ đứng $ABC \cdot A’B’C’$ có tất cả các cạnh bằng nhau. Góc giữa đường thẳng $AB’$ và mặt phẳng $\left( {A’B’C’} \right)$ bằng

A. ${30^ \circ }$.

B. ${90^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Câu 6: Cho $a$ là một số thực dương. Giá trị của biểu thức $P = {\left( {\sqrt {{2^a}} } \right)^{\frac{4}{a}}}$ bằng

A. 4 .

B. 2 .

C. 8 .

D. 1 .

Câu 7: Cho $lo{g_2}3 = a$. Khi đó $lo{g_3}18$ tính theo $a$ là

A. $\frac{a}{{2a + 1}}$.

B. $\frac{{2a + 1}}{a}$.

C. $2a + 1$.

D. $\frac{{a + 1}}{a}$.

Câu 8: Tập xác định của hàm số ${(x + 1)^{ – 2024}}$ là

A. $\left( { – 1; + \infty } \right)$

B. $\left[ { – 1; + \infty } \right)$

C. $\mathbb{R}$

D. $\mathbb{R} \setminus \left\{ { – 1} \right\}$

Câu 9: Cho $x$ là số thực dương. Biểu thức $\sqrt[4]{{{x^2}\sqrt[3]{x}}}$ được viết dưới dạng lũy thừa với số mũ hữu tỉ là

A. ${x^{\frac{{12}}{7}}}$.

B. ${x^{\frac{5}{6}}}$.

C. ${x^{\frac{7}{{12}}}}$.

D. ${x^{\frac{6}{5}}}$.

Câu 10: Với $a$ là số thực dương tùy ý, $ln\left( {5a} \right) – ln\left( {2a} \right)$ bằng

A. $\frac{{ln5}}{{ln2}}$.

B. $ln\left( {3a} \right)$.

C. $\frac{{ln5a}}{{ln2a}}$.

D. $ln\frac{5}{2}$.

Câu 11: Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = ln\left( {{x^2} – 2x + 10 – {m^2}} \right)$ xác định với mọi $x \in \mathbb{R}$.

A. 5 .

B. 7 .

C. 4 .

D. 0 .

Câu 12: Cho ba hàm số $y = {2^x},y = x,y = f\left( x \right)$ có đồ thị như hình bên, mệnh đề nào sau đây đúng?

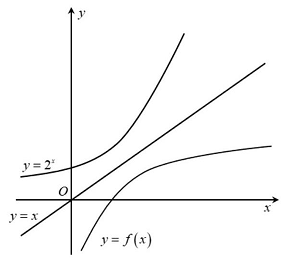
A. $y = f\left( x \right) = lo{g_{\frac{1}{2}}}x$.

B. $y = f\left( x \right) = lnx$.

C. $y = f\left( x \right) = lo{g_2}x$.

D. $y = f\left( x \right) = logx$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho các hàm số $y = lo{g_a}x,y = lo{g_b}x,y = lo{g_c}x$ với $a,b,c$ là ba số thực dương khác 1 . Xét tính đúng sai của các mệnh đề sau:

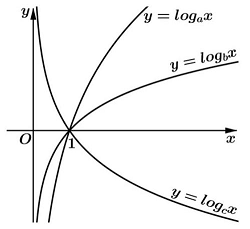
a) Đồ thị các hàm số trên đều đi qua điểm $A\left( {1;0} \right)$.

b) Hàm số $y = lo{g_c}x$ đồng biến trên khoảng $\left( {0; + \infty } \right)$

c) Từ đồ thị ta có: $0 < c < 1 < a < b$.

d) Đường thẳng $y = 3$ cắt hai đồ thị $y = lo{g_a}x,y = lo{g_b}x$ tại các điểm có hoành độ lần lượt là ${x_1};{x_2}$ sao cho ${x_2} = 2{x_1}$. Khi đó $\frac{a}{b} = \sqrt[3]{2}$.

Câu 2: Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$ và $SA = a\sqrt 5 $, đáy là tam giác vuông tại $A$ với $AB = a,AC = 2a$. Dựng $AK$ vuông góc $BC$ và $AH$ vuông góc $SK$.

a) Hai đường thẳng $BC$ và $AH$ vuông góc với nhau.

b) Đường thẳng $AH$ vuông góc với mặt phẳng $\left( {SBC} \right)$

c) Đoạn thẳng $AK$ có độ dài bằng $\frac{{a\sqrt 5 }}{5}$

d) Tan góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ bằng $\frac{2}{5}$.

Câu 3: Chọn ngẫu nhiên một lá bài từ bộ bài tú lơ khơ 52 lá, trả lại lá bài vừa rút vào bộ bài và rút tiếp một lá bài khác. Xét biến cố $A$ : “Lần đầu rút ra được lá Át” và $B$ : “Lần hai rút ra được là $Q$ “.

a) Hai biến cố $A$ và $B$ độc lập.

b) Xác suất của biến cố $A$ bằng $\frac{1}{{13}}$.

c) Xác suất để lần đầu rút lá Át và lần hai rút được lá $Q$ bằng $\frac{2}{{13}}$.

d) Xác suất trong hai lá bài rút ra không có đủ 2 lá chất rô bằng $\frac{{15}}{{16}}$.

Câu 4: Cho hình chóp $SABCD$ có đáy là hình chữ nhật tâm $I$ biết $AB = a,AD = 2a$. Gọi $M$ là trung điểm của $AB$ và $N$ là trung điểm của $MI$. Hình chiếu vuông góc của điểm $S$ lên mặt phẳng $\left( {ABCD} \right)$ trùng với điểm $N$. Biết góc tạo bởi đường thẳng $SB$ với mặt phẳng $\left( {ABCD} \right)$ bằng ${45^ \circ }$. Từ $N$ kẻ $NJ \bot AD,NH \bot SJ$.

a) Đường thẳng $AD$ vuông góc với mặt phẳng $\left( {SNJ} \right)$

b) Đường thẳng $NH$ vuông góc với mặt phẳng $\left( {SAD} \right)$

c) Tam giác $SBN$ là một tam giác vuông cân tại $S$

d) Khoảng cách giữa hai đường thẳng $MN$ và $SD$ theo $a$ là $\frac{{a\sqrt 6 }}{2}$

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Cho mẫu số liệu ghép nhóm thể hiện như bảng dưới đây

Nhóm	Tần số
$\left[ {2;4} \right)$	12
$\left[ {4;6} \right)$	15
$\left[ {6;8} \right)$	21
$\left[ {8;10} \right)$	18
$\left[ {10;12} \right)$	17
	83

Tính trung vị của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến hàng phần trăm).

Đáp án:

Câu 2: Hai người cùng bắn độc lập vào một mục tiêu. Xác suất bắn trúng của từng người lần lượt là 0,8 và 0,9 . Tìm xác suất của biến cố $A$ : “Chỉ có một người bắn trúng mục tiêu”.

Đáp án:

Câu 3: Cho hai số thực dương $a,b$. Rút gọn biểu thức $A = \frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}}$ ta thu được $A = {a^m}.{b^n}$. Tính $T = 9mn$.

Đáp án:

Câu 4: Một hộp đựng 4 viên bi màu đỏ và 6 viên bi màu xanh, các viên bi có đường kính khác nhau. Lấy ngẫu nhiên đồng thời 5 viên bi trong hộp. Xác suất để 5 viên bi được lấy ra có ít nhất 3 viên bi màu đỏ là $\frac{m}{n}$, với $m,n$ là các số nguyên dương, phân số $\frac{m}{n}$ tối giản. Tính $S = m + n$

Đáp án:

Câu 5: Mùa hè năm 2023, để chuẩn bị cho “học kỳ quân đội” dành cho các bạn nhỏ, một đơn vị bộ đội chuẩn bị thực phẩm cho các bạn nhỏ, dự kiến đủ dùng trong 45 ngày (năng suất ăn của mỗi ngày là như nhau). Nhưng bắt đầu từ ngày thứ 11 , do số lượng thành viên tham gia tăng lên, nên lượng thực phẩm tiêu thụ tăng lên $10{\text{\% }}$ mỗi ngày (ngày sau tăng $10{\text{\% }}$ so với ngày trước đó). Hỏi thực tế lượng thức ăn đó đủ dùng cho bao nhiêu ngày?

Đáp án:

Câu 6: Cho tứ diện $ABCD$ có $AB = CD = a,IJ = \frac{{a\sqrt 3 }}{2}$ ( $I,J$ lần lượt là trung điểm của $BC$ và $AD$ ). Tính số đo góc giữa hai đường thẳng $AB$ và $CD$.

ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

PHẦN I.

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Chọn	C	D	B	A	D	A	B	D	C	D	A	C

PHẦN II.

Câu 1	Câu 2	Câu 3	Câu 4
a) Đ	a) Đ	a) Đ	a) Đ
b) S	b) Đ	b) Đ	b) Đ
c) Đ	c) S	c) S	c) S
d) S	d) Đ	d) Đ	d) S

PHẦN III.

Câu	1	2	3	4	5	6
Chọn	7,38	0,26	1	53	25	60

GIẢI CHI TIẾT

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.

Câu 1: Khi gieo một đồng tiền (có hai mặt $S,N$ ) cân đối và đồng chất hai lần. Không gian mẫu của phép thử là:

A. $\left\{ {SS,NN,SN} \right\}$.

B. $\left\{ {SS,NN,NS} \right\}$.

C. $\left\{ {SS,NN,SN,NS} \right\}$.

D. $\left\{ {S,N} \right\}$.

Lời giải

Không gian mẫu của phép thử là: $\Omega = \left\{ {SS,NN,SN,NS} \right\}$.

Câu 2: Cho $A$ và $\overline A $ là hai biến cố đối nhau. Khẳng định nào sau đây đúng?

A. $P\left( A \right) + P\left( {\overline A } \right) = 0$.

B. $P\left( A \right) = – 1 + P\left( {\overline A } \right)$.

C. $P\left( A \right) = P\left( {\overline A } \right)$.

D. $P\left( A \right) = 1 – P\left( {\overline A } \right)$.

Lời giải

Vì $A$ và $\overline A $ là hai biến cố đối nhau nên $A \cup \overline A = \Omega $. Khi đó $P\left( A \right) + P\left( {\overline A } \right) = P\left( \Omega \right) = 1$.

Vậy $P\left( A \right) = 1 – P\left( {\overline A } \right)$.

Câu 3: Cho hình chóp $S.ABC$ có $SA$ vuông với đáy. Xác định góc giữa $SC$ và $\left( {ABC} \right)$.

A. $\widehat {SAC}$.

B. $\widehat {SCA}$.

C. $\widehat {ASC}$.

D. $\widehat {SCB}$.

Lời giải

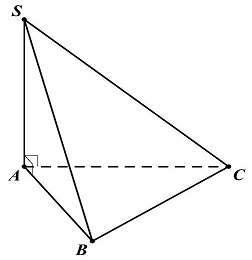
Ta có $\left\{ {\begin{array}{*{20}{l}}
{SA \bot \left( {ABC} \right)} \\
{SC \cap \left( {ABC} \right) = C}
\end{array}} \right.$

$ \Rightarrow AC$ là hình chiếu của $SC$ trên $\left( {ABC} \right)$. Do đó $\left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}$.

Câu 4: Khẳng định nào sau đây sai?

A. Nếu đường thẳng $\left( d \right)$ vuông góc với hai đường thẳng nằm trong $\left( \alpha \right)$ thì $d \bot \left( \alpha \right)$.

B. Nếu đường thẳng $d \bot \left( \alpha \right)$ thì $\left( d \right)$ vuông góc với mọi đường thẳng trong $\left( \alpha \right)$.

C. Nếu đường thẳng $\left( d \right)$ vuông góc với hai đường thẳng cắt nhau nằm trong $\left( \alpha \right)$ thì $\left( d \right)$ vuông góc với bất kì đường thẳng nào nằm trong $\left( \alpha \right)$.

D. Nếu $d \bot \left( \alpha \right)$ và đường thẳng $a//\left( \alpha \right)$ thì $d \bot a$.

Lời giải

Đáp án A sai vì thiếu điều kiện hai đường thẳng đó phải cắt nhau nằm trong $\left( \alpha \right)$.

Câu 5: Cho hình lăng trụ đứng $ABC \cdot A’B’C’$ có tất cả các cạnh bằng nhau. Góc giữa đường thẳng $AB’$ và mặt phẳng $\left( {A’B’C’} \right)$ bằng

A. ${30^ \circ }$.

B. ${90^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Lời giải

Góc giữa đường thẳng $AB’$ và mặt phẳng $\left( {A’B’C’} \right)$ bằng ${45^ \circ }$.

Câu 6: Cho $a$ là một số thực dương. Giá trị của biểu thức $P = {\left( {\sqrt {{2^a}} } \right)^{\frac{4}{a}}}$ bằng

A. 4 .

B. 2 .

C. 8 .

D. 1 .

Lời giải

Ta có $P = {\left( {\sqrt {{2^a}} } \right)^{\frac{4}{a}}} = {\left( {{2^{\frac{a}{2}}}} \right)^{\frac{4}{a}}} = {2^{\frac{4}{a} \cdot \frac{a}{2}}} = {2^2} = 4$.

Câu 7: Cho $lo{g_2}3 = a$. Khi đó $lo{g_3}18$ tính theo $a$ là

A. $\frac{a}{{2a + 1}}$.

B. $\frac{{2a + 1}}{a}$.

C. $2a + 1$.

D. $\frac{{a + 1}}{a}$.

Lời giải

Ta có $lo{g_3}18 = lo{g_3}9 + lo{g_3}2 = 2 + lo{g_3}2 = 2 + \frac{1}{{lo{g_2}3}} = 2 + \frac{1}{a} = \frac{{2a + 1}}{a}$.

Câu 8: Tập xác định của hàm số ${(x + 1)^{ – 2024}}$ là

A. $\left( { – 1; + \infty } \right)$

B. $\left[ { – 1; + \infty } \right)$

C. $\mathbb{R}$

D. $\mathbb{R} \setminus \left\{ { – 1} \right\}$

Lời giải

Vì -2024 là số nguyên âm nên hàm số xác định khi và chỉ khi $x + 1 \ne 0 \Leftrightarrow x \ne – 1$.

Vậy $D = \mathbb{R} \setminus \left\{ { – 1} \right\}$.

Câu 9: Cho $x$ là số thực dương. Biểu thức $\sqrt[4]{{{x^2}\sqrt[3]{x}}}$ được viết dưới dạng lũy thừa với số mũ hữu tỉ là

A. ${x^{\frac{{12}}{7}}}$.

B. ${x^{\frac{5}{6}}}$.

C. ${x^{\frac{7}{{12}}}}$.

D. ${x^{\frac{6}{5}}}$.

Ta có: $\sqrt[4]{{{x^2}\sqrt[3]{x}}} = \sqrt[4]{{{x^2} \cdot {x^{\frac{1}{3}}}}} = \sqrt[4]{{{x^{\frac{7}{3}}}}} = {x^{\frac{7}{{12}}}}$ với $x > 0$

Câu 10: Với $a$ là số thực dương tùy ý, $ln\left( {5a} \right) – ln\left( {2a} \right)$ bằng

A. $\frac{{ln5}}{{ln2}}.$.

B. $ln\left( {3a} \right)$.

C. $\frac{{ln5a}}{{ln2a}}$.

D. $ln\frac{5}{2}$.

Lòi giải

Ta có $ln\left( {5a} \right) – ln\left( {2a} \right) = ln\frac{{5a}}{{2a}} = ln\frac{5}{2}$.

Câu 11: Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = ln\left( {{x^2} – 2x + 10 – {m^2}} \right)$ xác định với mọi $x \in \mathbb{R}$.

A. 5 .

B. 7 .

C. 4 .

D. 0 .

Lời giải

Hàm số $y = ln\left( {{x^2} – 2x + 10 – {m^2}} \right)$ xác định với mọi $x \in \mathbb{R} \Leftrightarrow {x^2} – 2x + 10 – {m^2} > 0\forall x \in \mathbb{R}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta ‘ < 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 > 0} \\
{1 – \left( {10 – {m^2}} \right) < 0}
\end{array}} \right.} \right.$

$ \Leftrightarrow {m^2} – 9 < 0 \Leftrightarrow – 3 < m < 3$.

Do $m$ nguyên nên ta có 5 giá trị của $m$.

Câu 12: Cho ba hàm số $y = {2^x},y = x,y = f\left( x \right)$ có đồ thị như hình bên, mệnh đề nào sau đây đúng?

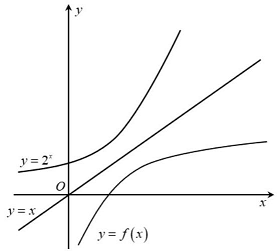
A. $y = f\left( x \right) = lo{g_{\frac{1}{2}}}x$.

B. $y = f\left( x \right) = lnx$.

C. $y = f\left( x \right) = lo{g_2}x$.

D. $y = f\left( x \right) = logx$.

Lời giải

Đồ thị hàm số $y = {2^x}$ và đồ thị hàm số $y = lo{g_2}x$ đối xứng nhau qua đường thẳng $y = x$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho các hàm số $y = lo{g_a}x,y = lo{g_b}x,y = lo{g_c}x$ với $a,b,c$ là ba số thực dương khác 1 . Xét tính đúng sai của các mệnh đề sau:

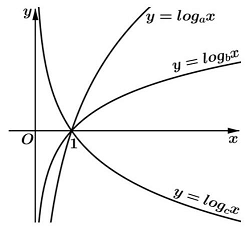
a) Đồ thị các hàm số trên đều đi qua điểm $A\left( {1;0} \right)$.

b) Hàm số $y = lo{g_c}x$ đồng biến trên khoảng $\left( {0; + \infty } \right)$

c) Từ đồ thị ta có: $0 < c < 1 < a < b$.

d) Đường thẳng $y = 3$ cắt hai đồ thị $y = lo{g_a}x,y = lo{g_b}x$ tại các điểm có hoành độ lần lượt là ${x_1};{x_2}$ sao cho ${x_2} = 2{x_1}$. Khi đó $\frac{a}{b} = \sqrt[3]{2}$.

Lời giải

Xét $lo{g_a}x = 1 \Leftrightarrow x = a;lo{g_b}x = 1 \Leftrightarrow x = b;lo{g_c} = 1 \Leftrightarrow x = c \Rightarrow c < 1 < a < b$.

a) Đúng: Đồ thị các hàm số trên đều đi qua điểm $A\left( {1;0} \right)$.

b) Sai: Hàm số $y = lo{g_c}x$ nghịch biến trên khoảng $\left( {0; + \infty } \right)$

c) Đúng: Từ đồ thị suy ra $0 < c < 1 < a < b$

d) Sai: Xét phương trình hoành độ giao điểm $lo{g_a}x = 3 \Leftrightarrow {x_1} = {a^3}$, và $lo{g_b}x = 3 \Leftrightarrow {x_2} = {b^3}$.

Do ${x_2} = 2{x_1}$ nên ${b^3} = 2{a^3}$ suy ra $\frac{a}{b} = \frac{1}{{\sqrt[3]{2}}}$.

Câu 2: Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$ và $SA = a\sqrt 5 $, đáy là tam giác vuông tại $A$ với $AB = a,AC = 2a$. Dựng $AK$ vuông góc $BC$ và $AH$ vuông góc $SK$.

a) Hai đường thẳng $BC$ và $AH$ vuông góc với nhau.

b) Đường thẳng $AH$ vuông góc với mặt phẳng $\left( {SBC} \right)$

c) Đoạn thẳng $AK$ có độ dài bằng $\frac{{a\sqrt 5 }}{5}$

d) Tan góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ bằng $\frac{2}{5}$.

Lời giải

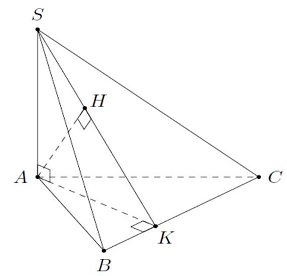
Ta có $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AK} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot AH} \right.$ mà $AH \bot SK$ nên $AH \bot \left( {SBC} \right)$.

Do đó $SK$ là hình chiếu vuông góc của $SA$ trên mặt phẳng $\left( {SBC} \right)$

Đăt $\alpha = \left( {SA;\left( {SBC} \right)} \right) = \left( {SA;SK} \right) = \widehat {ASK}$.

Ta có $AK = \frac{{AB \cdot AC}}{{BC}} = \frac{{AB \cdot AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \frac{{2a\sqrt 5 }}{5}$.

Khi đó $tan\alpha = \frac{{AK}}{{AS}} = \frac{{\frac{{2a\sqrt 5 }}{5}}}{{a\sqrt 5 }} = \frac{2}{5}$.

a) Đúng: Hai đường thẳng $BC$ và $AH$ vuông góc với nhau.

b) Đúng: Đường thẳng $AH$ vuông góc với mặt phẳng $\left( {SBC} \right)$

c) Sai: Đoạn thẳng $AK$ có độ dài bằng $\frac{{2a\sqrt 5 }}{5}$

d) Đúng: Tan góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ bằng $\frac{2}{5}$.

Câu 3: Chọn ngẫu nhiên một lá bài từ bộ bài tú lơ khơ 52 lá, trả lại lá bài vừa rút vào bộ bài và rút tiếp một lá bài khác. Xét biến cố $A$ : “Lần đầu rút ra được lá Át” và $B$ : “Lần hai rút ra được là $Q$ “.

a) Hai biến cố $A$ và $B$ độc lập.

b) Xác suất của biến cố $A$ bằng $\frac{1}{{13}}$.

c) Xác suất để lần đầu rút lá Át và lần hai rút được lá $Q$ bằng $\frac{2}{{13}}$.

d) Xác suất trong hai lá bài rút ra không có đủ 2 lá chất rô bằng $\frac{{15}}{{16}}$.

Lời giải

a) Đúng: Hai biến cố $A$ và $B$ độc lập.

Vì trả lại lá bài vừa rút được ở lần đầu vào bộ bài nên trong bộ bài vẫn có đủ 52 lá và 4 lá $Q$. Do đó xác suất của biến cố $B$ là $P\left( B \right) = \frac{{C_4^1}}{{C_{52}^1}} = \frac{4}{{52}} = \frac{1}{{13}}$.

Như vậy, xác suất xảy ra của biến cố $B$ không thay đổi bởi việc xảy ra hay không xảy ra của biến cố $A$.

Vì lần đầu lấy được lá Át nên $P\left( A \right) = \frac{{C_4^1}}{{C_{52}^1}} = \frac{4}{{52}} = \frac{1}{{13}}$ dù biến cố $B$ xảy ra hay không xảy ra.

Vậy $A$ và $B$ độc lập.

b) Đúng: Xác suất của biến cố $A$ bằng $\frac{1}{{13}}$ vì $P\left( A \right) = \frac{{C_4^1}}{{C_{52}^1}} = \frac{4}{{52}} = \frac{1}{{13}}$

c) Sai: Xác suất để lần đầu rút lá Át và lần hai rút được lá $Q$ bằng $\frac{1}{{169}}$.

Rút lá bài thứ nhất và trả lại vào bộ bài rồi rút lá bài thứ hai nên hai biến cố $A$ và $B$ độc lập.

$P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right) = \frac{{C_4^1}}{{C_{52}^1}} \cdot \frac{{C_4^1}}{{C_{52}^1}} = \frac{1}{{13}} \cdot \frac{1}{{13}} = \frac{1}{{169}}.$

d) Đúng: Xác suất trong hai lá bài rút ra không có đủ 2 lá chất rô bằng $\frac{{15}}{{16}}$.

Trong bộ bài tú lơ khơ 52 lá có 13 lá chất rô. Do đó, xác suất rút được 2 lá rô là $\frac{{13}}{{52}} \cdot \frac{{13}}{{52}} = \frac{1}{{16}}$

Vậy xác suất để 2 lá bài được rút không có đủ 2 lá chất rô là: $P = 1 – \frac{1}{{16}} = \frac{{15}}{{16}}$.

Câu 4: Cho hình chóp $SABCD$ có đáy là hình chữ nhật tâm $I$ biết $AB = a,AD = 2a$. Gọi $M$ là trung điểm của $AB$ và $N$ là trung điểm của $MI$. Hình chiếu vuông góc của điểm $S$ lên mặt phẳng $\left( {ABCD} \right)$ trùng với điểm $N$. Biết góc tạo bởi đường thẳng $SB$ với mặt phẳng $\left( {ABCD} \right)$ bằng ${45^ \circ }$. Từ $N$ kẻ $NJ \bot AD,NH \bot SJ$.

a) Đường thẳng $AD$ vuông góc với mặt phẳng $\left( {SNJ} \right)$

b) Đường thẳng $NH$ vuông góc với mặt phẳng $\left( {SAD} \right)$

c) Tam giác $SBN$ là một tam giác vuông cân tại $S$

d) Khoảng cách giữa hai đường thẳng $MN$ và $SD$ theo $a$ là $\frac{{a\sqrt 6 }}{2}$

Lời giải

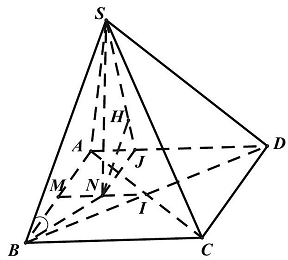
Ta có $MN//AD \Rightarrow MN//\left( {SAD} \right)$.

Nên $d\left( {MN,SD} \right) = d\left( {MN,\left( {SAD} \right)} \right) = d\left( {N,\left( {SAD} \right)} \right)$.

Ta được $\left. {\begin{array}{*{20}{c}}
{AD \bot NJ} \\
{AD \bot SN}
\end{array}} \right\} \Rightarrow AD \bot \left( {SNJ} \right),NH \subset \left( {SNJ} \right)$

$ \Rightarrow NH \bot AD,NH \bot SJ \Rightarrow NH \bot \left( {SAD} \right)$.

Nên $d\left( {MN,SD} \right) = d\left( {N,\left( {SAD} \right)} \right) = NH$.

Ta có $SN \bot \left( {ABCD} \right) \Rightarrow $ hình chiếu của $SB$ lên mặt phẳng $\left( {ABCD} \right)$ là $BN \Rightarrow \widehat {SBN} = {45^ \circ }$ là góc giữa $SB$ và mặt phẳng đáy.

Xét $\vartriangle BMN$ vuông ở $M$ có: $B{N^2} = B{M^2} + M{N^2}$

$ = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{2} \Rightarrow BN = \frac{a}{{\sqrt 2 }}$.

Xét $\vartriangle SBN$ vuông ở $N$ có $\widehat {SBN} = {45^ \circ } \Rightarrow \vartriangle SBN$ vuông cân tại $N \Rightarrow NB = NS = \frac{a}{{\sqrt 2 }}$.

Xét $\vartriangle SNJ$ vuông ở $N$ có: $\frac{1}{{N{H^2}}} = \frac{1}{{N{S^2}}} + \frac{1}{{N{J^2}}}$

$ = \frac{2}{{{a^2}}} + {\left( {\frac{2}{a}} \right)^2} = \frac{6}{{{a^2}}} \Rightarrow NH = \frac{{a\sqrt 6 }}{6}$.

a) Đúng: Đường thẳng $AD$ vuông góc với mặt phẳng $\left( {SNJ} \right)$

b) Đúng: Đường thẳng $NH$ vuông góc với mặt phẳng $\left( {SAD} \right)$

c) Sai: Tam giác $SBN$ là một tam giác vuông cân tại $N$

d) Sai: Khoảng cách giữa hai đường thẳng $MN$ và $SD$ theo $a$ là $\frac{{a\sqrt 6 }}{6}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Cho mẫu số liệu ghép nhóm thể hiện như bảng dưới đây

Nhóm	Tần số
$\left[ {2;4} \right)$	12
$\left[ {4;6} \right)$	15
$\left[ {6;8} \right)$	21
$\left[ {8;10} \right)$	18
$\left[ {10;12} \right)$	17

Tính trung vị của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến hàng phần trăm).

Lời giải

Lập lại bảng số liệu có tần số tích lũy ta có bảng sau:

Nhóm	Tần số	Tần số tích lũy
$\left[ {2;4} \right)$	12	12
$\left[ {4;6} \right)$	15	27
$\left[ {6;8} \right)$	21	48
$\left[ {8;10} \right)$	18	66
$\left[ {10;12} \right)$	17	83
	83

Do mẫu số liệu có 83 số liệu nên trung vị là số liệu nằm trong nhóm thứ 3 là nhóm $\left[ {6;8} \right)$.

Khi đó ta có

Số số liệu $n = 83$. Đầu mút trái $r = 6$.

Tần số nhóm thứ 3 là ${n_3} = 21$. Độ dài nhóm thứ 3 là $d = 2$.

Tần số tích lũy nhóm thứ 2 là $c{f_2} = 27$.

Áp dụng công thức ta có:

${M_e} = r + \left( {\frac{{\frac{n}{2} – c{f_{k – 1}}}}{{{n_k}}}} \right) \cdot d$

$ = 6 + \left( {\frac{{\frac{{83}}{2} – 27}}{{21}}} \right) \cdot 2 \approx 7,38$

Vậy trung vị của mẫu ghép nhóm là ${M_e} = 7,38$.

Câu 2: Hai người cùng bắn độc lập vào một mục tiêu. Xác suất bắn trúng của từng người lần lượt là 0,8 và 0,9 . Tìm xác suất của biến cố $A$ : “Chỉ có một người bắn trúng mục tiêu”.

Lời giải

Gọi ${A_1}$ là biến cố “Người 1 bắn trúng mục tiêu”.

Gọi ${A_2}$ là biến cố “Người 2 bắn trúng mục tiêu” $\left( {{A_1};{A_2};\overline {{A_1}} ;\overline {{A_2}} } \right.$ là các biến cố độc lập). Từ giả thiết ta có $P\left( {{A_1}} \right) = 0,8;P\left( {{A_2}} \right) = 0,9$.

Mà $A = {A_1}\overline {{A_2}} \cup \overline {{A_1}} {A_2}$

$ \Rightarrow P\left( A \right) = P\left( {{A_1}} \right) \cdot P\left( {\overline {{A_2}} } \right) + P\left( {\overline {{A_1}} } \right) \cdot P\left( {{A_2}} \right)$

$ = 0,8 \cdot \left( {1 – 0,9} \right) + \left( {1 – 0,8} \right) \cdot 0,9 = 0,26$.

Câu 3: Cho hai số thực dương $a,b$. Rút gọn biểu thức $A = \frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}}$ ta thu được $A = {a^m}.{b^n}$. Tính $T = 9mn$.

Lời giải

Ta có: $A = \frac{{{a^{\frac{1}{3}}}\sqrt b + {b^{\frac{1}{3}}}\sqrt a }}{{\sqrt[6]{a} + \sqrt[6]{b}}} = \frac{{{a^{\frac{1}{3}}}{b^{\frac{1}{2}}} + {b^{\frac{1}{3}}}{a^{\frac{1}{2}}}}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}}$

$ = \frac{{{a^{\frac{1}{3}}} \cdot {b^{\frac{1}{3}}}\left( {{b^{\frac{1}{6}}} + {a^{\frac{1}{6}}}} \right)}}{{{a^{\frac{1}{6}}} + {b^{\frac{1}{6}}}}} = {a^{\frac{1}{3}}} \cdot {b^{\frac{1}{3}}}$.

Do đó: $m = n = \frac{1}{3}$.

Vậy: $9m \cdot n = 9 \cdot \frac{1}{3} \cdot \frac{1}{3} = 1$.

Câu 4: Một hộp đựng 4 viên bi màu đỏ và 6 viên bi màu xanh, các viên bi có đường kính khác nhau. Lấy ngẫu nhiên đồng thời 5 viên bi trong hộp. Xác suất để 5 viên bi được lấy ra có ít nhất 3 viên bi màu đỏ là $\frac{m}{n}$, với $m,n$ là các số nguyên dương, phân số $\frac{m}{n}$ tối giản. Tính $S = m + n$

Lời giải

Lấy ngẫu nhiên đồng thời 5 viên bi từ 10 viên bi trong hộp.

Số phần tử không gian mẫu $n\left( \Omega \right) = {\text{C}}_{10}^5$.

Gọi $A$ là biến cố lấy được ít nhất 3 viên bi đỏ.

Trường hợp 1: Lấy 3 bi đỏ từ 4 bi đỏ và 2 bi xanh từ 6 bi xanh có ${\text{C}}_4^3 \cdot {\text{C}}_6^2$ cách.

Trường hợp 2: Lấy 4 bi đỏ từ 4 bi đỏ và 1 bi xanh từ 6 bi xanh có ${\text{C}}_4^4 \cdot {\text{C}}_6^1$ cách.

Suy ra $n\left( {{\Omega _A}} \right) = {\text{C}}_4^3 \cdot {\text{C}}_6^2 + {\text{C}}_4^4 \cdot {\text{C}}_6^1$.

Xác suất để 5 viên bi được lấy ra có ít nhất 3 viên bi màu đỏ bằng $P\left( A \right) = \frac{{n\left( {{\Omega _A}} \right)}}{{n\left( \Omega \right)}} = \frac{{11}}{{42}}$.

Vậy $\left\{ {\begin{array}{*{20}{l}}
{m = 11} \\
{n = 42}
\end{array} \Rightarrow S = m + n = 53} \right.$.

Câu 5: Mùa hè năm 2023, để chuẩn bị cho “học kỳ quân đội” dành cho các bạn nhỏ, một đơn vị bộ đội chuẩn bị thực phẩm cho các bạn nhỏ, dự kiến đủ dùng trong 45 ngày (năng suất ăn của mỗi ngày là như nhau). Nhưng bắt đầu từ ngày thứ 11 , do số lượng thành viên tham gia tăng lên, nên lượng thực phẩm tiêu thụ tăng lên $10{\text{\% }}$ mỗi ngày (ngày sau tăng $10{\text{\% }}$ so với ngày trước đó). Hỏi thực tế lượng thức ăn đó đủ dùng cho bao nhiêu ngày?

Lời giải

Dự kiến tiêu thụ $x > 0$ lượng thực phẩm trong 1 ngày.

Suy ra lượng thức ăn dự kiến có là $45x$.

Lượng thức ăn dùng trong 10 ngày đầu là $10x$.

Lượng thức ăn dùng trong ngày thứ 11 là $x + x.10{\text{\% }} = 1,1x$.

Lượng thức ăn dùng trong ngày thứ 12 là $1,1x + 1,1x \cdot 10{\text{\% }} = 1,{1^2}x$.

Lượng thức ăn dùng trong ngày thứ 13 là $1,{1^3}x$.

Lượng thức ăn dùng trong ngày thứ $10 + n$ là $1,{1^n} \cdot x$.

Tổng lượng thức ăn dùng trong các ngày cho đến khi hết là

$10x + 1,1x + 1,{1^2}x + \ldots + 1,{1^n}x = 45x \Leftrightarrow 1,1 + 1,{1^2} + \ldots + 1,{1^n} = 35$

$ \Leftrightarrow \frac{{1,1\left( {1 – 1,{1^n}} \right)}}{{1 – 1,1}} = 35 \Leftrightarrow 1 – 1,{1^n} = – \frac{{35 \cdot 0,1}}{{1,1}}$

$ \Leftrightarrow 1,{1^n} = 1 + \frac{{3,5}}{{1,1}} \Leftrightarrow n \approx 15$.

Vậy lượng thực phẩm đã chuẩn bị dùng đủ trong $10 + 15 = 25$ ngày.

Câu 6: Cho tứ diện $ABCD$ có $AB = CD = a,IJ = \frac{{a\sqrt 3 }}{2}$ ( $I,J$ lần lượt là trung điểm của $BC$ và $AD$ ). Tính số đo góc giữa hai đường thẳng $AB$ và $CD$.

Lời giải

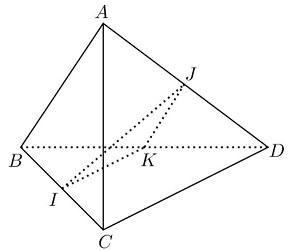
Gọi $K$ là trung điểm của $BD$. Khi đó $IK$ song song với $CD$ và $JK$ song song với $AB$.

Khi đó $\widehat {\left( {AB,CD} \right)} = \widehat {\left( {KI,KJ} \right)} = \left[ {\begin{array}{*{20}{l}}
{\widehat {IKJ}} \\
{{{180}^ \circ } – \widehat {IKJ}}
\end{array}} \right.$.

Ta có $KI = KJ = \frac{a}{2}$

$ \Rightarrow {\text{cos}}\widehat {IKJ} = \frac{{K{I^2} + K{J^2} – I{J^2}}}{{2KI \cdot KJ}}$

$ = \frac{{\frac{{{a^2}}}{4} + \frac{{{a^2}}}{4} – \frac{{3{a^2}}}{4}}}{{2 \cdot \frac{a}{2} \cdot \frac{a}{2}}} = – \frac{1}{2}$.

Vậy $\widehat {IKJ} = {120^ \circ } \Rightarrow \widehat {\left( {AB,CD} \right)} = {60^ \circ }$.