Đề Thi Giữa HK2 Toán 11 Kết Nối Tri Thức Giải Chi Tiết-Đề 2

Đề thi giữa HK2 Toán 11 Kết nối tri thức giải chi tiết-Đề 2 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12 . Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.

Câu 1: Tìm tập xác định của hàm số $y = {\left( {{x^2} – 4} \right)^{ – 2024}}$.

A. $\left( { – \infty ; – 2} \right) \cup \left( {2; + \infty } \right)$. B. $\left( {2; + \infty } \right)$. C. $\mathbb{R} \setminus \left\{ { \pm 2} \right\}$. D. $\left( { – \infty ; – 2} \right)$.

Câu 2: Giả sử $a,b$ và $\alpha $ là các số thực tùy ý $(a > 0,b > 0)$. Mệnh đề nào sau đây đúng?

A. ${(ab)^\alpha } = {a^\alpha } + {b^\alpha }$. B. ${(a + b)^\alpha } = {a^\alpha } + {b^\alpha }$. C. ${(ab)^\alpha } = {a^\alpha } \cdot {b^\alpha }$. D. ${\left( {\frac{a}{b}} \right)^\alpha } = {a^\alpha } \cdot {b^{\frac{1}{\alpha }}}$.

Câu 3: Cho khối lăng trụ có diện tích đáy bằng. ${a^2}$.và khoảng cách giữa hai đáy bằng $3a$. Tính thể tích $V$ của khối lăng trụ đã cho.

A. $V = \frac{3}{2}{a^3}$. B. $V = 3{a^3}$. C. $V = {a^3}$. D. $V = 9{a^3}$.

Câu 4: Với $a$ là số thực dương tùy ý, ${log_2}{a^2} + {log_4}a$ bằng

A. $\frac{3}{2}{log_2}a$. B. $\frac{5}{2}{log_2}a$. C. ${log_2}a$. D. $\frac{1}{2}{log_2}a$.

Câu 5: Một khối chóp tứ giác đều có chiều cao bằng 6 và cạnh đáy bằng 2 . Thể tích của khối chóp đó bằng

A. 12 . B. 8 . C. 24 . D. 6 .

Câu 6: Cho các hàm số $y = {a^x},y = {log_b}x,y = {log_c}x$ có đồ thị như hình vẽ bên. Chọn khẳng định đúng?

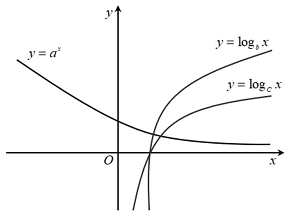
A. $b > c > a$. B. $b > a > c$. C. $a > b > c$ D. $c > b > a$.

Câu 7: Nghiệm của phương trình ${log_3}x = \frac{1}{3}$ là

A. $x = 27$. B. $x = \sqrt[3]{3}$. C. $x = \frac{1}{3}$. D. $x = \frac{1}{{27}}$.

Câu 8: Tập nghiệm của bất phương trình ${2^{2 + {x^2}}} > 16$ là

A. $\left( { – \infty ; – 2} \right) \cup \left( {2; + \infty } \right)$. B. $\left( { – \infty ; – \sqrt 2 } \right) \cup \left( {\sqrt 2 ; + \infty } \right)$.

C. $\left( { – \infty ; – 2\left] \cup \right[2; + \infty } \right)$. D. $\left( { – \infty ; – \sqrt 2 \left] \cup \right[\sqrt 2 ; + \infty } \right)$.

Câu 9: Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Mệnh đề nào sau đây là sai?

A. Nếu $b \bot \left( P \right)$ thì $b//a$. B. Nếu $b//\left( P \right)$ thì $b \bot a$.

C. Nếu $b//a$ thì $b \bot \left( P \right)$. D. Nếu $b \bot a$ thì $b//\left( P \right)$.

Câu 10: Cho hình chóp $S.ABCD$ có đáy là hình vuông, cạnh bên $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Khẳng định nào sau đây sai?

A. $BD \bot \left( {SAC} \right)$. B. $SA \bot \left( {ABC} \right)$. C. $CD \bot \left( {SBC} \right)$. D. $BC \bot \left( {SAB} \right)$.

Câu 11: Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông cạnh $a,SA$ vuông góc với đáy, $SA = a$. Khoảng cách giữa hai đường thẳng $SB$ và $CD$ là

A. $a\sqrt 3 $. B. $a\sqrt 2 $. C. $2a$. D. $a$.

Câu 12: Cho hình chóp $S \cdot ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Biết $SA \bot \left( {ABC} \right)$ và $SA = a\sqrt 3 $. Thể tích khối chóp $S.ABC$ là

A. $\frac{{3{a^3}}}{4}$. B. $\frac{{{a^3}}}{4}$. C. $\frac{{{a^3}\sqrt 3 }}{6}$. D. $\frac{{{a^3}\sqrt 3 }}{4}$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho phương trình ${log_3}\left( {{3^x} – 1} \right) \cdot {log_{27}}\left( {{3^{x + 2}} – 9} \right) = m$ với $m$ là tham số. Xét tính đúng sai của các mệnh đề sau.

a) Điều kiện xác định của phương trình là $x \geqslant 0$.

b) Khi $m = 1$ phương trình có một nghiệm là $x = {log_3}2$.

c) Đặt ${log_3}\left( {{3^x} – 1} \right) = t$. Khi đó phương trình đã cho trở thành ${t^2} + 2t – 3m = 0$.

d) Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi $m > – \frac{1}{3}$.

Câu 2: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $C$. Tam giác $SAB$ vuông cân tại $S$ và $\widehat {BSC} = {60^ \circ };SA = a$. Gọi $M,N$ lần lượt là trung điểm cạnh $SB,SA,\varphi $ là góc giữa đường thẳng $AB$ và $CM$.

a) Độ dài đoạn thẳng $AB$ bằng $a\sqrt 3 $

b) Tam giác $SBC$ là tam giác đều

c) Đường thẳng $MN$ song song với đường thẳng $AB$ và $\widehat {\left( {AB,CM} \right)} = \overline {\left( {MN,CM} \right)} $

d) Cosin góc tạo bởi hai đường thẳng $AB$ và $CM$ bằng $\frac{{\sqrt 6 }}{8}$

Câu 3: Ông $X$ gửi vào ngân hàng số tiền 300 triệu đồng theo hình thức lãi kép với lãi suất $6\% $ /năm. Xét tính đúng sai của các mệnh đề sau.

a) Số tiền lãi ông $X$ nhận được ở năm đầu tiên là 6 triệu đồng.

b) Công thức tính số tiền ông $X$ nhận được cả gốc và lãi sau $n$ năm gửi tiền là ${T_n} = 300000000.{(1 + 6\% )^n}$ đồng.

c) Số tiền ông $X$ nhận được sau 5 năm là nhiều hơn 410 triệu đồng.

d) Nếu ông $X$ muốn nhận được số tiền cả gốc lẫn lãi nhiều hơn 500 triệu đồng thì cần gửi ít nhất 9 năm.

Câu 4: Cho khối chóp đều $S \cdot ABCD$ có $AC = 4a$, hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ vuông góc với nhau. Gọi $M,O,N$ lần lượt là trung điểm của $AB,AC,CD$, qua $S$ dựng đường thẳng $Sx//AB$.

a) Đường thẳng. $Sx$. vuông góc với mặt phẳng $\left( {SMN} \right)$

b) Tứ giác $ABCD$ là một hình bình hành

c) Đoạn thẳng $SO$ có độ dài bằng $a\sqrt 2 $

d) Thể tích khối chóp $S.ABCD$ bằng $\frac{{{a^3}\sqrt 2 }}{3}$

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Biết ${4^x} + {4^{ – x}} = 14$. Hãy tính giá trị của biểu thức $P = {2^x} + {2^{ – x}}$.

Đáp án:

Câu 2: Cho $a,b$ là các số thực dương và $a$ khác 1 , thỏa mãn ${log_{{a^3}}}\frac{{{a^5}}}{{\sqrt[4]{b}}} = 2$. Giá trị của biểu thức ${log_a}b$ bằng bao nhiêu?

Đáp án:

Câu 3: Sau một tháng thi công, công trình xây dựng lớp học từ thiện cho học sinh vùng cao đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công trình và kịp thời đưa vào sử dụng, đơn vị xây dựng quyết định từ tháng thứ hai tăng $4\% $ khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công?

Câu 4: Cho lăng trụ đứng $ABC \cdot A’B’C’$ có đáy $ABC$ là tam giác vuông tại $B$ có $AC = a\sqrt 3 $, cạnh bên $AA’ = 3a$. Tính góc giữa đường thẳng $A’C$ và mặt phẳng $\left( {ABC} \right)$.

Đáp án:

Câu 5: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,AB = 1,BC = \sqrt 2 ,SA$ vuông góc với mặt phẳng đáy và $SA = \sqrt 2 $. Tính khoảng cách giữa hai đường thẳng $AB$ và $SC$.

Đáp án:

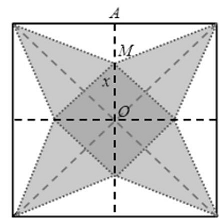
Câu 6: Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết các cạnh hình vuông bằng $20\;cm,OM = x\left( {\;cm} \right)$. Tìm $x$ để hình chóp đều ấy có thể tích lớn nhất (đơn vị: cm)

ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

PHẦN I.

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Chọn	C	C	B	B	B	D	B	D	D	C	D	B

PHẦN II.

Câu 1	Câu 2	Câu 3	Câu 4
a) S	a) S	a) S	a) Đ
b) S	b) Đ	b) Đ	b) S
c) Đ	c) Đ	c) S	c) Đ
d) Đ	d) S	d) Đ	d) S

PHẦN III.

Câu	$1$	$2$	$3$	$4$	$5$	$6$
Chọn	4	-4	18	60	1	8

HƯỚNG DẪN GIẢI CHI TIẾT

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phưong án.

Câu 1: Tìm tập xác định của hàm số $y = {\left( {{x^2} – 4} \right)^{ – 2024}}$.

A. $\left( { – \infty ; – 2} \right) \cup \left( {2; + \infty } \right)$.

B. $\left( {2; + \infty } \right)$.

C. $\mathbb{R} \setminus \left\{ { \pm 2} \right\}$.

D. $\left( { – \infty ; – 2} \right)$.

Lời giải

Hàm số xác định $ \Leftrightarrow {x^2} – 4 \ne 0 \Leftrightarrow x \ne \pm 2$.

Vậy $D = \mathbb{R} \setminus \left\{ { \pm 2} \right\}$.

Câu 2: Giả sử $a,b$ và $\alpha $ là các số thực tùy ý $(a > 0,b > 0)$. Mệnh đề nào sau đây đúng?

A. ${(ab)^\alpha } = {a^\alpha } + {b^\alpha }$.

B. ${(a + b)^\alpha } = {a^\alpha } + {b^\alpha }$.

C. ${(ab)^\alpha } = {a^\alpha } \cdot {b^\alpha }$.

D. ${\left( {\frac{a}{b}} \right)^\alpha } = {a^\alpha } \cdot {b^{\frac{1}{\alpha }}}$.

Lời giải

Công thức đúng: ${(ab)^\alpha } = {a^\alpha } \cdot {b^\alpha }$.

Câu 3: Cho khối lăng trụ có diện tích đáy bằng. ${a^2}$.và khoảng cách giữa hai đáy bằng $3a$. Tính thể tích $V$ của khối lăng trụ đã cho.

A. $V = \frac{3}{2}{a^3}$.

B. $V = 3{a^3}$.

C. $V = {a^3}$.

D. $V = 9{a^3}$.

Lời giải

Ta có chiều cao lăng trụ $h = 3a$.

Thể tích của khối lăng trụ $V = Bh = 3{a^3}$.

Câu 4: Với $a$ là số thực dương tùy ý, ${log_2}{a^2} + {log_4}a$ bằng

A. $\frac{3}{2}{log_2}a$.

B. $\frac{5}{2}{log_2}a$.

C. ${log_2}a$.

D. $\frac{1}{2}{log_2}a$.

Lời giải

Ta có ${log_2}{a^2} + {log_4}a = 2{log_2}a + \frac{1}{2}{log_2}a = \frac{5}{2}{log_2}a$.

Câu 5: Một khối chóp tứ giác đều có chiều cao bằng 6 và cạnh đáy bằng 2. Thể tích của khối chóp đó bằng

A. 12 .

B. 8 .

C. 24 .

D. 6 .

Lời giải

Thể tích của khối chóp đã cho là $V = \frac{1}{3}{S_{day}} \cdot h = \frac{1}{3} \cdot {2^2} \cdot 6 = 8$

Câu 6: Cho các hàm số $y = {a^x},y = {log_b}x,y = {log_c}x$ có đồ thị như hình vẽ bên. Chọn khẳng định đúng?

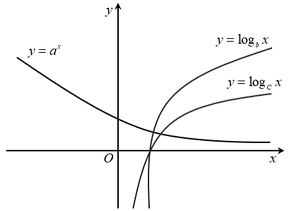
A. $b > c > a$.

B. $b > a > c$.

C. $a > b > c$

D. $c > b > a$.

Lời giải

Hàm $y = {a^x}$ nghịch biến nên $0 < a < 1$.

Hàm $y = {log_b}x,y = {log_c}x$ đồng biến nên $b,c > 1$

Đường thẳng $y = 1$ cắt ĐTHS $y = {log_c}x,y = {log_b}x$ tại các điểm có hoành độ lần lượt là $c$ và $b$. Ta thấy $b < c$.

Câu 7: Nghiệm của phương trình ${log_3}x = \frac{1}{3}$ là

A. $x = 27$.

B. $x = \sqrt[3]{3}$.

C. $x = \frac{1}{3}$.

D. $x = \frac{1}{{27}}$.

Lời giải

Ta có: ${log_3}x = \frac{1}{3} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \geqslant 0} \\
{x = {3^{\frac{1}{3}}}}
\end{array} \Leftrightarrow x = \sqrt[3]{3}} \right.$.

Câu 8: Tập nghiệm của bất phương trình ${2^{2 + {x^2}}} > 16$ là

A. $\left( { – \infty ; – 2} \right) \cup \left( {2; + \infty } \right)$.

B. $\left( { – \infty ; – \sqrt 2 } \right) \cup \left( {\sqrt 2 ; + \infty } \right)$.

C. $\left( { – \infty ; – 2\left] \cup \right[2; + \infty } \right)$.

D. $\left( { – \infty ; – \sqrt 2 \left] \cup \right[\sqrt 2 ; + \infty } \right)$.

Lời giải

Ta có. ${2^{2 + {x^2}}} > 16 \Leftrightarrow 2 + {x^2} > 4 \Leftrightarrow {x^2} > 2$

$ \Leftrightarrow x \in \left( { – \infty ; – \sqrt 2 } \right) \cup \left( {\sqrt 2 ; + \infty } \right)$

Câu 9: Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Mệnh đề nào sau đây là sai?

A. Nếu $b \bot \left( P \right)$ thì $b//a$.

B. Nếu $b//\left( P \right)$ thì $b \bot a$.

C. Nếu $b//a$ thì $b \bot \left( P \right)$.

D. Nếu $b \bot a$ thì $b//\left( P \right)$.

Lời giải

Nếu $b \bot a$ thì $b//\left( P \right)$.

Câu 10: Cho hình chóp $S.ABCD$ có đáy là hình vuông, cạnh bên $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Khẳng định nào sau đây sai?

A. $BD \bot \left( {SAC} \right)$.

B. $SA \bot \left( {ABC} \right)$.

C. $CD \bot \left( {SBC} \right)$.

D. $BC \bot \left( {SAB} \right)$.

Lời giải

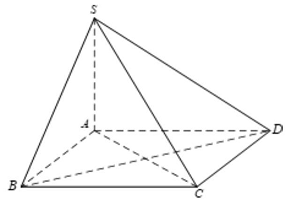
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{CD \bot AD} \\
{CD \bot SA}
\end{array} \Rightarrow CD \bot \left( {SAD} \right)} \right.$ mà theo đáp án $C$ có $CD \bot \left( {SBC} \right),\left( {SBC} \right)$ và $\left( {SAD} \right)$ có điểm chung $S$ nên $\left( {SBC} \right)$ và $\left( {SAD} \right)$ trùng nhau. Vô lý vậy C sai.

$\left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow } \right.$ A đúng.

$\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow } \right.$ D đúng.

$SA \bot \left( {ABCD} \right) \Rightarrow SA \bot \left( {ABC} \right) \Rightarrow B$ đúng.

Câu 11: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a,SA$ vuông góc với đáy, $SA = a$. Khoảng cách giữa hai đường thẳng $SB$ và $CD$ là

A. $a\sqrt 3 $.

B. $a\sqrt 2 $.

C. $2a$.

D. $a$.

Lời giải

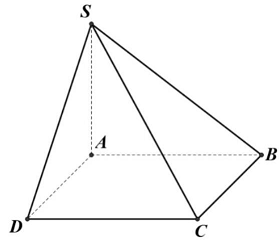
Vì $CD//AB$ nên $d\left( {SB,CD} \right) = d\left( {CD,\left( {SAB} \right)} \right) = d\left( {D,\left( {SAB} \right)} \right) = AD = a$.

Câu 12: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Biết $SA \bot \left( {ABC} \right)$ và $SA = a\sqrt 3 $. Thể tích khối chóp $S.ABC$ là

A. $\frac{{3{a^3}}}{4}$.

B. $\frac{{{a^3}}}{4}$.

C. $\frac{{{a^3}\sqrt 3 }}{6}$.

D. $\frac{{{a^3}\sqrt 3 }}{4}$.

Lời giải

Ta có ${V_{S.ABC}} = \frac{1}{3} \cdot SA \cdot {S_{\vartriangle ABC}} = \frac{1}{3} \cdot a\sqrt 3 \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}}}{4}$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho phương trình ${log_3}\left( {{3^x} – 1} \right) \cdot {log_{27}}\left( {{3^{x + 2}} – 9} \right) = m$ với $m$ là tham số. Xét tính đúng sai của các mệnh đề sau.

a) Điều kiện xác định của phương trình là $x \geqslant 0$.

b) Khi $m = 1$ phương trình có một nghiệm là $x = {log_3}2$.

c) Đặt ${log_3}\left( {{3^x} – 1} \right) = t$. Khi đó phương trình đã cho trở thành ${t^2} + 2t – 3m = 0$.

d) Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi $m > – \frac{1}{3}$.

Lời giải

a) Sai: Điều kiện xác định: $\left\{ {\begin{array}{*{20}{l}}
{{3^x} – 1 > 0} \\
{{3^{x + 2}} – 9 > 0}
\end{array} \Leftrightarrow x > 0} \right.$.

b) Sai: Khi $m = 1$ phương trình có dạng:

${log_3}\left( {{3^x} – 1} \right) \cdot {log_{27}}\left( {{3^{x + 2}} – 9} \right) = 1$

$ \Leftrightarrow {log_3}\left( {{3^x} – 1} \right) \cdot {log_{{3^3}}}\left[ {{3^2}\left( {{3^x} – 1} \right)} \right] = 1$

$ \Leftrightarrow {log_3}\left( {{3^x} – 1} \right) \cdot \left[ {{log_3}\left( {{3^x} – 1} \right) + 2} \right] = 3$

$ \Leftrightarrow {\left[ {{log_3}\left( {{3^x} – 1} \right)} \right]^2} + 2{log_3}\left( {{3^x} – 1} \right) – 3 = 0$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{log_3}\left( {{3^x} – 1} \right) = 1} \\
{{log_3}\left( {{3^x} – 1} \right) = – 3}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{3^x} – 1 = 3} \\
{{3^x} – 1 = \frac{1}{{27}}}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{3^x} = 4} \\
{{3^x} = \frac{{28}}{{27}}}
\end{array}} \right.} \right.} \right.$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = {log_3}4} \\
{x = {log_3}\frac{{28}}{{27}}}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 2{log_3}2} \\
{x = {log_3}\frac{{28}}{{27}}}
\end{array}} \right.} \right.$

c) Đúng: ${log_3}\left( {{3^x} – 1} \right) \cdot {log_{27}}\left( {{3^{x + 2}} – 9} \right) = m$

$ \Leftrightarrow {log_3}\left( {{3^x} – 1} \right) \cdot {log_{{3^3}}}\left[ {{3^2}\left( {{3^x} – 1} \right)} \right] = m$

$ \Leftrightarrow {log_3}\left( {{3^x} – 1} \right) \cdot \left[ {{log_3}\left( {{3^x} – 1} \right) + 2} \right] = 3m$

$ \Leftrightarrow {\left[ {{log_3}\left( {{3^x} – 1} \right)} \right]^2} + 2{log_3}\left( {{3^x} – 1} \right) – 3m = 0$

Khi đó đặt ${log_3}\left( {{3^x} – 1} \right) = t$ thì phương trình đã cho trở thành ${t^2} + 2t – 3m = 0\;\left( 1 \right)$.

d) Đúng: Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt $ \Leftrightarrow \Delta ‘ = 1 + 3m > 0 \Leftrightarrow m > – \frac{1}{3}$.

Câu 2: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $C$. Tam giác $SAB$ vuông cân tại $S$ và $\widehat {BSC} = {60^ \circ };SA = a$. Gọi $M,N$ lần lượt là trung điểm cạnh $SB,SA,\varphi $ là góc giữa đường thẳng $AB$ và $CM$.

a) Độ dài đoạn thẳng $AB$ bằng $a\sqrt 3 $

b) Tam giác $SBC$ là tam giác đều

c) Đường thẳng $MN$ song song với đường thẳng $AB$ và $\widehat {\left( {AB,CM} \right)} = \widehat {\left( {MN,CM} \right)}$

d) Cosin góc tạo bởi hai đường thẳng $AB$ và $CM$ bằng $\frac{{\sqrt 6 }}{8}$

Lời giải

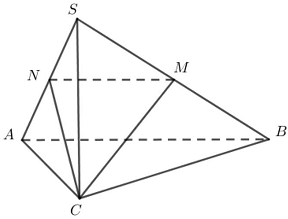
Đặt $SA = a$. Suy ra $SB = CA = CB = a$ và $AB = a\sqrt 2 $.

Lại có $\widehat {BSC} = {60^ \circ }$. Suy ra tam giác $SBC$ dều nên $SC = a$.

Suy ra $CM = CN = \frac{{a\sqrt 3 }}{2}$ hay $MN$ song song với $AB$.

Khi đó $\widehat {\left( {AB,CM} \right)} = \left( {\widehat {MN,CM}} \right)$. Áp dụng định lí cosin vào tam giác $CMN$ ta có:

$cos\widehat {CMN} = \frac{{M{C^2} + M{N^2} – C{N^2}}}{{2MC \cdot MN}} = \frac{{\sqrt 6 }}{6}$

$ \Rightarrow cos\left( {AB,CM} \right) = cos\left( {MN,CM} \right) = \left| {cos\widehat {CMN}} \right| = \frac{{\sqrt 6 }}{6}$.

a) Sai: Độ dài đoạn thẳng $AB$ bằng $a\sqrt 2 $

b) Đúng: Tam giác $SBC$ là tam giác đều

c) Đúng: Đường thẳng $MN$ song song với đường thẳng $AB$ và $\widehat {\left( {AB,CM} \right)} = \widehat {\left( {MN,CM} \right)}$

d) Sai: Cosin góc tạo bởi hai đường thẳng $AB$ và $CM$ bằng $\frac{{\sqrt 6 }}{6}$

Câu 3: Ông $X$ gửi vào ngân hàng số tiền 300 triệu đồng theo hình thức lãi kép với lãi suất $6\% $ /năm. Xét tính đúng sai của các mệnh đề sau.

a) Số tiền lãi ông $X$ nhận được ở năm đầu tiên là 6 triệu đồng.

b) Công thức tính số tiền ông $X$ nhận được cả gốc và lãi sau $n$ năm gửi tiền là ${T_n} = 300000000 \cdot {(1 + 6\% )^n}$ đồng.

c) Số tiền ông $X$ nhận được sau 5 năm là nhiều hơn 410 triệu đồng.

d) Nếu ông $X$ muốn nhận được số tiền cả gốc lẫn lãi nhiều hơn 500 triệu đồng thì cần gửi ít nhất 9 năm.

Lời giải

a) Sai: Vì số tiền lãi năm đầu tiên bằng số tiền gửi nhân với lãi suất: $300 \times 6\% = 18$ triệu đồng.

b) Đúng: Áp dụng công thức: ${T_n} = A \cdot {(1 + r)^n}$.

Theo giả thiết $A = 3000000;r = 6\% $ nên suy ra số tiền nhận được cả gốc và lãi sau $n$ năm gửi tiền là ${T_n} = 300000000.{(1 + 6\% )^n}$ đồng

c) Sai: Vì số tiền ông nhận được sau 5 năm gửi là ${T_5} = 300000000 \cdot {(1 + 6\% )^5} \approx 401467673$ đồng, nhỏ hơn 410 triệu đồng.

d) Đúng: Công thức tính số tiền nhận được cả gốc và lãi sau $n$ năm gửi tiền là ${T_n} = 300000000.{(1 + 6\% )^n}$ đồng.

Theo giả thiết ta có ${T_n} > 500000000 \Leftrightarrow 300000000 \cdot {(1 + 6\% )^n} > 500000000$

$ \Leftrightarrow n > {log_{\left( {1 + 6\% } \right)}}\frac{5}{3} \approx 8,77$.

Vậy sau ít nhất 9 năm thì ông $X$ thu được số tiền cả gốc lẫn lãi nhiều hơn 500 triệu đồng.

Câu 4: Cho khối chóp đều $S.ABCD$ có $AC = 4a$, hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ vuông góc với nhau. Gọi $M,O,N$ lần lượt là trung điểm của $AB,AC,CD$, qua $S$ dựng đường thẳng $Sx//AB$.

a) Đường thẳng. $Sx$. vuông góc với mặt phẳng $\left( {SMN} \right)$

b) Tứ giác $ABCD$ là một hình bình hành

c) Đoạn thẳng $SO$ có độ dài bằng $a\sqrt 2 $

d) Thể tích khối chóp $S \cdot ABCD$ bằng $\frac{{{a^3}\sqrt 2 }}{3}$

Lời giải

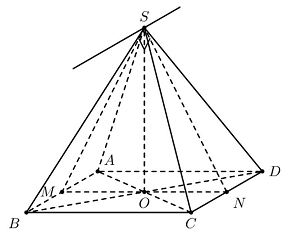
Gọi $M,O,N$ lần lượt là trung điểm của $AB,AC,CD$ nên $AB \bot SM,CD \bot SN$.

Qua $S$ dựng đường thẳng $Sx//AB$.

Vì $\left\{ {\begin{array}{*{20}{l}}
{AB \subset \left( {SAB} \right)} \\
{CD \subset \left( {SCD} \right)} \\
{AB//CD}
\end{array}} \right.$ nên $\left( {SAB} \right) \cap \left( {SCD} \right) = Sx//AB//CD$

Ta có $\left\{ {\begin{array}{*{20}{l}}
{Sx \bot SM} \\
{Sx \bot SN}
\end{array} \Rightarrow Sx \bot \left( {SMN} \right) \Rightarrow \widehat {MSN} = {{90}^ \circ }} \right.$.

Hình chóp $S.ABCD$ đều $ \Rightarrow ABCD$ là hình vuông, có $AC = 4a \Rightarrow AB = BC = \frac{{AC}}{{\sqrt 2 }} = 2a\sqrt 2 $

$ \Rightarrow MN = 2\sqrt 2 a \Rightarrow SO = \frac{{MN}}{2} = a\sqrt 2 $.

Vậy thể tích khối chóp $S \cdot ABCD$ là $V = \frac{1}{3} \cdot SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot \sqrt 2 a \cdot {(2a\sqrt 2 )^2} = \frac{{8\sqrt 2 }}{3}{a^3}$.

a) Đúng: Đường thẳng $Sx$ vuông góc với mặt phẳng $\left( {SMN} \right)$

b) Sai: Tứ giác $ABCD$ là một hình vuông do khối chóp này là khối chóp đều

c) Đúng: Đoạn thẳng $SO$ có độ dài bằng $2a\sqrt 2 $

d) Sai: Thể tích khối chóp $S.ABCD$ bằng $\frac{{8{a^3}\sqrt 2 }}{3}$

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .

Câu 1: Biết ${4^x} + {4^{ – x}} = 14$. Hãy tính giá trị của biểu thức $P = {2^x} + {2^{ – x}}$.

Lời giải

Ta có ${4^x} + {4^{ – x}} = 14 \Leftrightarrow {\left( {{2^x}} \right)^2} + {\left( {{2^{ – x}}} \right)^2} + 2 = 16$

$ \Leftrightarrow {\left( {{2^x} + {2^{ – x}}} \right)^2} = 16 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{2^x} + {2^{ – x}} = 4} \\
{{2^x} + {2^{ – x}} = – 4}
\end{array}} \right.$

$ \Leftrightarrow {2^x} + {2^{ – x}} = 4$ (vì ${2^x} + {2^{ – x}} > 0,\forall x \in \mathbb{R}$ ).

Vậy $P = 4$.

Câu 2: Cho $a,b$ là các số thực dương và $a$ khác 1 , thỏa mãn ${log_{{a^3}}}\frac{{{a^5}}}{{\sqrt[4]{b}}} = 2$. Giá trị của biểu thức ${log_a}b$ bằng bao nhiêu?

Lò̀i giải

Ta có: $2 = {log_{{a^3}}}\frac{{{a^5}}}{{\sqrt[4]{b}}} = \frac{1}{3}{log_a}\frac{{{a^5}}}{{{b^{\frac{1}{4}}}}}$

$ = \frac{1}{3}\left( {{log_a}{a^5} – {log_a}{b^{\frac{1}{4}}}} \right) = \frac{1}{3}\left( {5 – \frac{1}{4}{log_a}b} \right)$

$ \Rightarrow 5 – \frac{1}{4}{log_a}b = 6 \Rightarrow {log_a}b = – 4$.

Câu 3: Sau một tháng thi công, công trình xây dựng lớp học từ thiện cho học sinh vùng cao đã thực hiện được một khối lượng công việc. Nếu tiếp tục với tiến độ như vậy thì dự kiến sau đúng 23 tháng nữa công trình sẽ hoàn thành. Để sớm hoàn thành công trình và kịp thời đưa vào sử dụng, đơn vị xây dựng quyết định từ tháng thứ hai tăng $4\% $ khối lượng công việc so với tháng kề trước. Hỏi công trình sẽ hoàn thành ở tháng thứ mấy sau khi khởi công?

Lời giải

Theo dự kiến, cần 24 tháng để hoàn thành công trình. Vậy khối lượng công việc trên một tháng theo dự tính là: $\frac{1}{{24}}$ ( công trình )

Khối lượng công việc của tháng thứ 2 là: ${T_2} = \frac{1}{{24}} + 0,04 \cdot \frac{1}{{24}} = \frac{1}{{24}}{(1 + 0,04)^1}$

Khối lượng công việc của tháng thứ 3 là:

${T_3} = \left( {\frac{1}{{24}} + 0,04 \cdot \frac{1}{{24}}} \right) + 0,04 \cdot \left( {\frac{1}{{24}} + 0,04 \cdot \frac{1}{{24}}} \right) = \frac{1}{{24}} \cdot {(1 + 0,04)^2}$

Như vậy khối lượng công việc của tháng thứ $n$ là: ${T_n} = \frac{1}{{24}} \cdot {(1 + 0,04)^{n – 1}}$

Ta có: $\frac{1}{{24}} \cdot {(1 + 0,04)^0} + \frac{1}{{24}} \cdot {(1 + 0,04)^1} + \ldots + \frac{1}{{24}} \cdot {(1 + 0,04)^{n – 1}} = 1$

$ \Leftrightarrow \frac{1}{{24}} \cdot \frac{{1 – {{(1 + 0,04)}^n}}}{{1 – \left( {1 + 0,04} \right)}} = 1 \Leftrightarrow {(1 + 0,04)^n} = \frac{{49}}{{25}}$

$ \Leftrightarrow n = {log_{1 + 0,04}}\frac{{49}}{{25}} \approx 17,2$

Vậy công trình sẽ hoàn thành ở tháng thứ 18 từ khi khởi công.

Câu 4: Cho lăng trụ đứng $ABC \cdot A’B’C’$ có đáy $ABC$ là tam giác vuông tại $B$ có $AC = a\sqrt 3 $, cạnh bên $AA’ = 3a$. Tính góc giữa đường thẳng $A’C$ và mặt phẳng $\left( {ABC} \right)$.

Lời giải

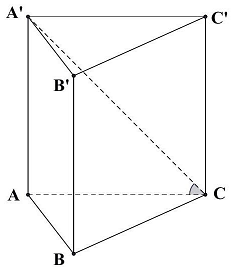
Ta có hình chiếu của $A’C$ lên mặt phẳng $\left( {ABC} \right)$ là $AC$.

Nên $\left( {A’C,\left( {ABC} \right)} \right) = \left( {A’C,AC} \right) = \widehat {A’CA}$. Ta có $tan\widehat {A’CA} = \frac{{A’A}}{{AC}} = \frac{{3a}}{{a\sqrt 3 }} = \sqrt 3 \Rightarrow \widehat {A’CA} = {60^ \circ }$.

Do vậy $\left( {A’C,\left( {ABC} \right)} \right) = {60^ \circ }$.

Câu 5: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,AB = 1,BC = \sqrt 2 ,SA$ vuông góc với mặt phẳng đáy và $SA = \sqrt 2 $. Tính khoảng cách giữa hai đường thẳng $AB$ và $SC$.

Lời giải

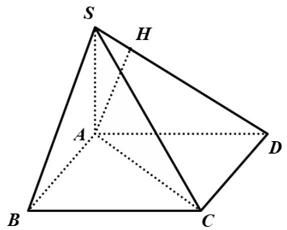
Dựng điểm $D$ sao cho $ABCD$ là hình chữ nhật. Ta có $AB//CD$ nên $AB//\left( {SCD} \right)$.

Khi đó $d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right)$.

Trong $\left( {SCD} \right)$, dựng $AH \bot SD\left( {H \in SD} \right)$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{CD \bot AD} \\
{CD \bot SA}
\end{array} \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH} \right.$.

Có $\left\{ {\begin{array}{*{20}{l}}
{AH \bot SD} \\
{AH \bot CD}
\end{array} \Rightarrow AH \bot \left( {SCD} \right)} \right.$.
Do đó $d\left( {A,\left( {SCD} \right)} \right) = AH$.

Ta có $AD = BC = \sqrt 2 $.

$\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{2{a^2}}} + \frac{1}{{2{a^2}}} = \frac{1}{{{a^2}}} \Rightarrow AH = a$. Vậy $d\left( {AB,SC} \right) = AH = 1$.

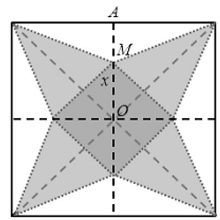
Câu 6: Cắt một miếng giấy hình vuông như hình bên và xếp thành hình một hình chóp tứ giác đều. Biết các cạnh hình vuông bằng $20\;cm,OM = x\left( {\;cm} \right)$. Tìm $x$ để hình chóp đều ấy có thể tích lớn nhất (đơn vị: cm)

Lời giải

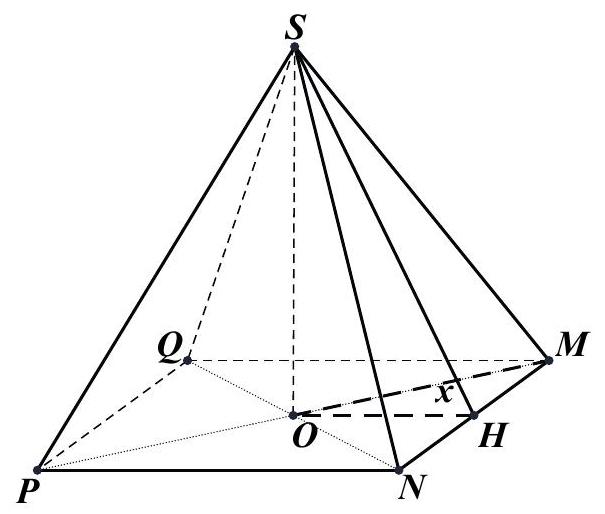
Giả sử được hình chóp tứ giác đều như hình vẽ có cạnh đáy bằng $x\sqrt 2 $.

Khi đó: $OM = x \Rightarrow OH = HM = \frac{x}{{\sqrt 2 }} \Rightarrow SH = 10\sqrt 2 – \frac{x}{{\sqrt 2 }}$.

Suy ra: $SO = \sqrt {S{H^2} – O{H^2}} = \sqrt {{{\left( {10\sqrt 2 – \frac{x}{{\sqrt 2 }}} \right)}^2} – {{\left( {\frac{x}{{\sqrt 2 }}} \right)}^2}} = \sqrt {20\left( {10 – x} \right)} $.

Thể tích $V = \frac{1}{3} \cdot {S_{MNPQ}} \cdot SO = \frac{1}{3} \cdot 2{x^2} \cdot \sqrt {20\left( {10 – x} \right)} $

$ = \frac{{\sqrt {20} }}{3} \cdot {x^2} \cdot \sqrt {40 – 4x} $ (với $0 \leqslant x \leqslant 10$ ).

Tìm giá trị lớn nhất của $V$ ta được ${V_{max}} = \frac{{\sqrt {20} }}{3} \cdot {10^2}$ khi $x = 8$.

Có thể tìm giá trị lớn nhất bằng cách áp dụng BĐT Cauchy cho 4 số không âm, ta có:

${x^2} \cdot \sqrt {40 – 4x} = \sqrt {\left( {40 – 4x} \right) \cdot x \cdot x \cdot x \cdot x} $

$ \leqslant {\left( {\sqrt {\frac{{40 – 4x + x + x + x + x}}{4}} } \right)^4} \Leftrightarrow \sqrt {40 – 4x} \cdot {x^2} \leqslant {10^2}$

Vậy $V = \frac{{\sqrt {20} }}{3} \cdot {x^2}\sqrt {40 – 4x} \leqslant \frac{{\sqrt {20} }}{3} \cdot {10^2}$. Dấu bằng xảy ra khi $40 – 4x = x \Leftrightarrow x = 8$.