Đề Kiểm Tra Giữa Học Kỳ 2 Toán 11 Chân Trời Sáng Tạo Giải Chi Tiết-Đề 1

Đề kiểm tra giữa học kỳ 2 Toán 11 Chân trời sáng tạo giải chi tiết-Đề 1 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Giá trị của ${27^{\frac{1}{3}}}$ bằng:

A. 6 . B. 81 . C. 9 . D. 3 .

Câu 2: Hàm số $y = {(x – 1)^{\frac{1}{3}}}$ có tập xác định là

A. $\left[ {1; + \infty } \right)$. B. $\left( {1; + \infty } \right)$. C. $\left( { – \infty ; + \infty } \right)$. D. $\left( { – \infty ;1} \right) \cup \left( {1; + \infty } \right)$.

Câu 3: Thể tích của khối chóp có diện tích đáy bằng $B$ và chiều cao bằng $h$ là

A. $V = Bh$. B. $V = \frac{1}{3}Bh$. C. $V = \frac{\pi }{3}Bh$. D. $V = \frac{1}{3}\pi {B^2}h$.

Câu 4: Cho $a > 0$ thỏa mãn $loga = 7$. Giá trị của $log\left( {100a} \right)$ bằng

A. 9 . B. 700 . C. 14 . D. 7 .

Câu 5: Tìm $a$ để đồ thị hàm số $y = {log_a}x(0 < a \ne 1)$ có đồ thị là hình bên.

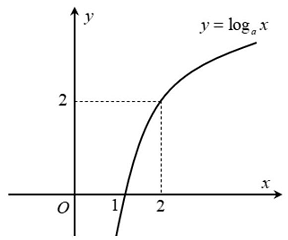
A. $a = \sqrt 2 $. B. $a = \frac{1}{{\sqrt 2 }}$. C. $a = \frac{1}{2}$. D. $a = 2$

Câu 6: Tổng các nghiệm của phương trình ${3^{{x^2} – 2x – 5}} = 27$ là

A. 0 . B. -8 C. -2 . D. 2 .

Câu 7: Cho khối hộp chữ nhật có kích thước 2;4;6. Thể tích của khối hộp đã cho bằng

A. 16 . B. 12 . C. 48 . D. 8 .

Câu 8: Tìm tập nghiệm của bất phương trình: ${log_2}\left( {2 – x} \right) \leqslant 1$.

A. $\left[ {0; + \infty } \right)$. B. $\left[ {0;2} \right]$. C. $\left( { – \infty ;2} \right)$. D. $\left[ {0;2} \right)$.

Câu 9: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Góc giữa hai đường thẳng $BA’$ và $CD$ bằng

A. ${45^ \circ }$. B. ${60^ \circ }$. C. ${30^ \circ }$. D. ${90^ \circ }$.

Câu 10: Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Trong các mệnh đề dưới đây, mệnh đề nào sai?

A. Nếu $b//a$ thì $b \bot \left( P \right)$. B. Nếu $b \subset \left( P \right)$ thì $b \bot a$.

C. Nếu $b//\left( P \right)$ thì $b \bot a$. D. Nếu $b//a$ thì $b//\left( P \right)$.

Câu 11: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng 2 , cạnh bên bằng 3 . Gọi $\varphi $ là góc giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?

A. $tan\varphi = \sqrt 7 $. B. $\varphi = {60^0}$. C. $\varphi = {45^0}$. D. $cos\varphi = \frac{{\sqrt 2 }}{3}$.

Câu 12: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt phẳng đáy và $SA = a\sqrt 2 $. Thể tích của khối chóp đã cho bằng

A. ${a^3}\sqrt 2 $. B. $\frac{{{a^3}\sqrt 2 }}{3}$. C. $\frac{{{a^3}\sqrt 2 }}{4}$. D. $\frac{{{a^3}\sqrt 2 }}{6}$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho phương trình: $log_2^2\left( {x + 1} \right) – 6{log_2}\sqrt {x + 1} + 2 = 0$. Xét tính đúng sai của các mệnh đề sau:

a) Điều kiện xác định của phương trình là $x > – 1$.

b) Nếu đặt $t = {log_2}\left( {x + 1} \right)$ thì phương trình đã cho trở thành ${t^2} – 6t + 2 = 0$.

c) Phương trình đã cho có hai nghiệm nguyên dương.

d) Tổng các nghiệm của phương trình đã cho bằng 6 .

Câu 2: Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B,SA \bot \left( {ABC} \right),AB = BC = a$, $SA = a\sqrt 3 $. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ ?

a) Đường thẳng $BC$ vuông góc với đường thẳng $SB$.

b) Góc tạo bởi hai đường thẳng $SB$ và $AB$ bằng góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$.

c) Cosin góc tạo bởi hai đường thẳng $SB$ và $AB$ bằng $\frac{{\sqrt 3 }}{2}$

d) Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ bằng ${45^ \circ }$.

Câu 3: Hình vẽ dưới đây là đồ thị của các hàm số mũ $y = {a^x},y = {b^x},y = {c^x}$

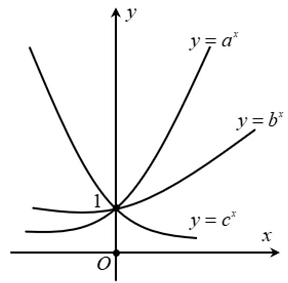
a) Từ đồ thị, hàm số $y = {a^x}$ là hàm số nghịch biến.

b) Hàm số $y = {c^x}$ là hàm số nghịch biến nên $c < 1$.

c) Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến nên $a < b$.

d) Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến và $y = {c^x}$ là hàm số nghịch biến nên ta suy ra được $a > b > 1 > c$.

Câu 4: Cho hình chóp $S.ABC$ có $SA$ vuông góc với đáy, hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ vuông góc với nhau, $SB = a\sqrt 3 $, góc giữa $SC$ và $\left( {SAB} \right)$ là ${45^ \circ }$ và $\widehat {ASB} = {30^ \circ }$.

a) Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng .

b) Tam giác $SBC$ vuông cân tại $C$.

c) Hai đường thẳng $AB$ và $CB$ vuông góc với nhau.

d) Nếu gọi thể tích khối chóp $S.ABC$ là $V$ thì tỷ số $\frac{{{a^3}}}{V}$ bằng $\frac{3}{8}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .

Câu 1: Có bao nhiêu giá trị nguyên của tham số $m \in \left( { – 2024;2024} \right)$ để hàm số $y = {\left( {{x^2} – 2x – m + 1} \right)^{\sqrt 7 }}$ có tập xác định là $\mathbb{R}$ ?

Câu 2: Tìm số nghiệm nguyên của bất phương trình ${log_{2 – \sqrt 3 }}\left( {x – 1} \right) + {log_{2 + \sqrt 3 }}\left( {11 – 2x} \right) \geqslant 0$.

Câu 3: Số lượng của loại vi khuẩn $A$ trong một phòng thí nghiệm được tính theo công thức $S\left( t \right) = S\left( 0 \right){.2^t}$, trong đó $S\left( 0 \right)$ là số lượng vi khuẩn $A$ ban đầu, $S\left( t \right)$ là số lượng vi khuẩn $A$ có sau $t$ phút. Biết sau 3 phút thì số lượng vi khuẩn $A$ là 625 nghìn con. Hỏi sau bao lâu (đơn vị: phút) kể từ lúc ban đầu, số lượng vi khuẩn $A$ là 10 triệu con?

Câu 4: Cho hình chóp $S.ABC$ có $BC = a\sqrt 2 $ các cạnh còn lại đều bằng $a$. Tính góc giữa hai đường thẳng $SB$ và $AC$ (đơn vị: độ)

Câu 5: Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng 4 . Tính khoảng cách giữa hai đường thẳng $AB’$ và $CD’$

Câu 6: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh 3 và đường chéo $AC = 3$. Tam giác $SAB$ cân tại $S$ và nằm trong mặt phẳng vuông góc với đáy. Góc giữa $\left( {SCD} \right)$ và đáy bằng ${45^ \circ }$. Tính thể tích của khối chóp $S.ABCD$ (đơn vị thể tích).

GIẢI CHI TIẾT

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.

Câu 1: Giá trị của ${27^{\frac{1}{3}}}$ bằng

A. 6.

B. 81 .

C. 9 .

D. 3 .

Lời giải

Ta có ${27^{\frac{1}{3}}} = \sqrt[3]{{27}} = 3$.

Câu 2: Hàm số $y = {(x – 1)^{\frac{1}{3}}}$ có tập xác định là

A. $\left[ {1; + \infty } \right)$.

B. $\left( {1; + \infty } \right)$.

C. $\left( { – \infty ; + \infty } \right)$.

D. $\left( { – \infty ;1} \right) \cup \left( {1; + \infty } \right)$.

Lời giải

Vì $\frac{1}{3}$ là số không nguyên nên hàm số $y = {(x – 1)^{\frac{1}{3}}}$ xác định khi và chỉ khi $x – 1 > 0 \Leftrightarrow x > 1$.

Vậy hàm số $y = {(x – 1)^{\frac{1}{3}}}$ có tập xác định là $\left( {1; + \infty } \right)$.

Câu 3: Thể tích của khối chóp có diện tích đáy bằng $B$ và chiều cao bằng $h$ là

A. $V = Bh$.

B. $V = \frac{1}{3}Bh$.

C. $V = \frac{\pi }{3}Bh$.

D. $V = \frac{1}{3}\pi {B^2}h$.

Lời giải

Ta có công thức $V = \frac{1}{3}Bh$.

Câu 4: Cho $a > 0$ thỏa mãn $loga = 7$. Giá trị của $log\left( {100a} \right)$ bằng

A. 9 .

B. 700 .

C. 14 .

D. 7 .

Lời giải

Ta có: $log\left( {100a} \right) = log100 + loga = 2 + loga = 2 + 7 = 9$.

Câu 5: Tìm $a$ để đồ thị hàm số $y = {log_a}x(0 < a \ne 1)$ có đồ thị là hình bên.

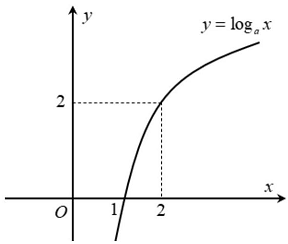
A. $a = \sqrt 2 $.

B. $a = \frac{1}{{\sqrt 2 }}$.

C. $a = \frac{1}{2}$.

D. $a = 2$

Do đồ thị hàm số đi qua điểm $\left( {2;2} \right)$ nên $2 = {log_a}2 \Leftrightarrow a = \sqrt 2 $.

Câu 6: Tổng các nghiệm của phương trình ${3^{{x^2} – 2x – 5}} = 27$ là

A. 0 .

B. -8 .

C. -2 .

D. 2 .

Lời giải

Ta có: ${3^{{x^2} – 2x – 5}} = 27 \Leftrightarrow {3^{{x^2} – 2x – 5}} = {3^3} \Leftrightarrow {x^2} – 2x – 8 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 2} \\
{x = 4}
\end{array}} \right.$.

Vậy $4 + \left( { – 2} \right) = 2$.

Câu 7: Cho khối hộp chữ nhật có kích thước $2;4;6$. Thể tích của khối hộp đã cho bằng

A. 16 .

B. 12 .

C. 48 .

D. 8 .

Lời giải

Thể tích của khối hộp là $V = 2 \cdot 4.6 = 48$.

Câu 8: Tìm tập nghiệm của bất phương trình: ${log_2}\left( {2 – x} \right) \leqslant 1$.

A. $\left[ {0; + \infty } \right)$.

B. $\left[ {0;2} \right]$.

C. $\left( { – \infty ;2} \right)$.

D. $\left[ {0;2} \right)$.

Lời giải

Tập xác định $D = \left( { – \infty ;2} \right)$. Ta có: ${log_2}\left( {2 – x} \right) \leqslant 1 \Leftrightarrow 2 – x \leqslant 2 \Leftrightarrow x \geqslant 0$. Vậy $S = \left[ {0;2} \right)$.

Câu 9: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Góc giữa hai đường thẳng $BA’$ và $CD$ bằng

A. ${45^ \circ }$.

B. ${60^ \circ }$.

C. ${30^ \circ }$.

D. ${90^ \circ }$.

Lời giải

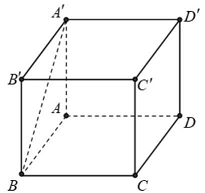
Vì $CD//AB$ nên $\left( {BA’,CD} \right) = \left( {BA’,BA} \right) = \widehat {ABA’} = {45^ \circ }$ (do $ABB’A’$ là hình vuông).

Câu 10: Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Trong các mệnh đề dưới đây, mệnh đề nào sai?

A. Nếu $b//a$ thì $b \bot \left( P \right)$.

B. Nếu $b \subset \left( P \right)$ thì $b \bot a$.

C. Nếu $b//\left( P \right)$ thì $b \bot a$.

D. Nếu $b//a$ thì $b//\left( P \right)$.

Lời giải

A. Đúng vì $\left\{ {\begin{array}{*{20}{l}}
{a \bot \left( P \right)} \\
{a//b}
\end{array} \Rightarrow b \bot \left( P \right)} \right.$ nên đáp án D sai.

B. Đúng vì $\left\{ {\begin{array}{*{20}{l}}
{a \bot \left( P \right)} \\
{b \subset \left( P \right)}
\end{array} \Rightarrow a \bot b} \right.$.

C. Đúng vì $\left\{ {\begin{array}{*{20}{l}}
{a \bot \left( P \right)} \\
{b//\left( P \right)}
\end{array} \Rightarrow b \bot a} \right.$.

Câu 11: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng 2 , cạnh bên bằng 3 . Gọi $\varphi $ là góc giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?

A. $tan\varphi = \sqrt 7 $.

B. $\varphi = {60^0}$.

C. $\varphi = {45^0}$.

D. $cos\varphi = \frac{{\sqrt 2 }}{3}$.

Lời giải

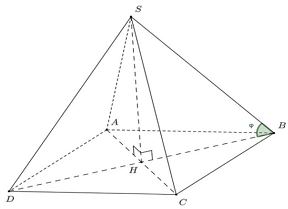
Gọi $H = AB \cap CD \Rightarrow SH \bot \left( {ABCD} \right) \Rightarrow \varphi = \left( {SB,\left( {ABCD} \right)} \right) = \widehat {SAH}$.

Xét tam giác $SBH$ vuông tại $H$, có $BH = \frac{{BD}}{2} = \frac{{2\sqrt 2 }}{2} = \sqrt 2 $.

$ \Rightarrow cos\varphi = \frac{{BH}}{{SB}} = \frac{{\sqrt 2 }}{3}$.

Câu 12: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt phẳng đáy và $SA = a\sqrt 2 $. Thể tích của khối chóp đã cho bằng

A. ${a^3}\sqrt 2 $.

B. $\frac{{{a^3}\sqrt 2 }}{3}$.

C. $\frac{{{a^3}\sqrt 2 }}{4}$.

D. $\frac{{{a^3}\sqrt 2 }}{6}$.

Lời giải

Diện tích đáy ${S_{ABCD}} = {a^2}$.

Thể tích của khối chóp đã cho là ${V_{S \cdot ABCD}} = \frac{1}{3}SA \cdot {S_{ABCD}} = \frac{1}{3}a\sqrt 2 \cdot {a^2} = \frac{{{a^3}\sqrt 2 }}{3}$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho phương trình: $log_2^2\left( {x + 1} \right) – 6{log_2}\sqrt {x + 1} + 2 = 0$. Xét tính đúng sai của các mệnh đề sau:

a) Điều kiện xác định của phương trình là $x > – 1$.

b) Nếu đặt $t = {log_2}\left( {x + 1} \right)$ thì phương trình đã cho trở thành ${t^2} – 6t + 2 = 0$.

c) Phương trình đã cho có hai nghiệm nguyên dương.

d) Tổng các nghiệm của phương trình đã cho bằng 6

Lời giải

Điều kiện: $x > – 1$.

Ta có: $log_2^2\left( {x + 1} \right) – 6{log_2}\sqrt {x + 1} + 2 = 0 \Leftrightarrow log_2^2\left( {x + 1} \right) – 3{log_2}\left( {x + 1} \right) + 2 = 0$

Đặt $t = {log_2}\left( {x + 1} \right)$ thì phương trình trở thành ${t^2} – 3t + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 1} \\
{t = 2}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1} \\
{x = 3}
\end{array}} \right.} \right.$.

So với điều kiện thấy thỏa mãn. Vậy tổng các nghiệm là: $1 + 3 = 4$.

a) Đúng: Điều kiện xác định của phương trình là $x > – 1$.

b) Sai: Nếu đặt $t = {log_2}\left( {x + 1} \right)$ thì phương trình đã cho trở thành ${t^2} – 3t + 2 = 0$.

c) Đúng: Phương trình đã cho có hai nghiệm nguyên dương là $x = 1$ hoặc $x = 3$

d) Sai: Tổng các nghiệm của phương trình đã cho bằng 4 .

Câu 2: Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B,SA \bot \left( {ABC} \right),AB = BC = a$, $SA = a\sqrt 3 $. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ ?

a) Đường thẳng $BC$ vuông góc với đường thẳng $SB$.

b) Góc tạo bởi hai đường thẳng $SB$ và $AB$ bằng góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$

c) Cosin góc tạo bởi hai đường thẳng $SB$ và $AB$ bằng $\frac{{\sqrt 3 }}{2}$

d) Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ bằng ${45^ \circ }$

Lời giải

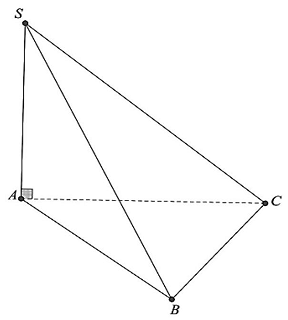
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{SA \bot BC\;\left( {\;do\;SA \bot \left( {ABC} \right)} \right)} \\
{AB \bot BC\;\left( {gt} \right)}
\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB} \right.$

Xét 2 mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ ta có: $\left\{ {\begin{array}{*{20}{l}}
{\left( {SBC} \right) \cap \left( {ABC} \right) = BC} \\
{SB \bot BC,SB \subset \left( {SBC} \right)} \\
{AB \bot BC,AB \subset \left( {ABC} \right)} \\
{SB \cap AB = \left\{ B \right\}}
\end{array}} \right.$.

$ \Rightarrow \left( {\widehat {\left( {SBA} \right);\left( {ABC} \right)}} \right) = \left( {\widehat {SB,AB}} \right) = \widehat {SBA}$

Xét $SAB$ tam giác vuông tại $A$, có $tan\widehat {SBA} = \frac{{SA}}{{AB}} = \sqrt 3 \Rightarrow \widehat {SBA} = {60^ \circ }$.

a) Đúng: Đường thẳng $BC$ vuông góc với đường thẳng $SB$.

b) Đúng: Góc tạo bởi hai đường thẳng $SB$ và $AB$ bằng góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$

c) Sai: Cosin góc tạo bởi hai đường thẳng $SB$ và $AB$ bằng $\frac{{\sqrt 3 }}{2}$

d) Sai: Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ bằng ${45^ \circ }$.

Câu 3: Hình vẽ dưới đây là đồ thị của các hàm số mũ $y = {a^x},y = {b^x},y = {c^x}$

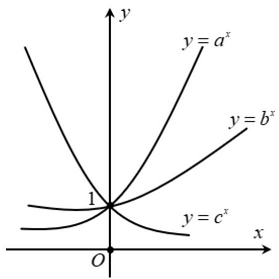
a) Từ đồ thị, hàm số $y = {a^x}$ là hàm số nghịch biến.

b) Hàm số $y = {c^x}$ là hàm số nghịch biến nên $c < 1$.

c) Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến nên $a < b$.

d) Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến và $y = {c^x}$ là hàm số nghịch biến nên ta suy ra được $a > b > 1 > c$.

Lời giải

Từ đồ thị ta suy ra: Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến và $y = {c^x}$ là hàm số nghịch biến.

Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến nên $a,b > 1$

Do $y = {c^x}$ là hàm số nghịch biến nên $c < 1$.

Nếu lấy $x = m$ khi đó tồn tại ${y_1},{y_2} > 0$ để $\left\{ {\begin{array}{*{20}{l}}
{{a^m} = {y_1}} \\
{{b^m} = {y_2}}
\end{array}} \right.$. Dễ thấy ${y_1} > {y_2}$ nên $a > b$.

Vậy $a > b > 1 > c$

a) Sai: Từ đồ thị, hàm số $y = {a^x}$ là hàm số đồng biến.

b) Đúng: Hàm số $y = {c^x}$ là hàm số nghịch biến nên $c < 1$.

c) Sai: Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến nên $a > b$.

d) Đúng: Hai hàm số $y = {a^x}$ và $y = {b^x}$ là hai hàm số đồng biến và $y = {c^x}$ là hàm số nghịch biến nên ta suy ra được $a > b > 1 > c$.

Câu 4: Cho hình chóp $S.ABC$ có $SA$ vuông góc với đáy, hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ vuông góc với nhau, $SB = a\sqrt 3 $, góc giữa $SC$ và $\left( {SAB} \right)$ là ${45^ \circ }$ và $\widehat {ASB} = {30^ \circ }$.

a) Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng

b) Tam giác $SBC$ vuông cân tại $C$

c) Hai đường thẳng $AB$ và $CB$ vuông góc với nhau.

d) Nếu gọi thể tích khối chóp $S.ABC$ là $V$ thì tỷ số $\frac{{{a^3}}}{V}$ bằng $\frac{3}{8}$.

Lời giải

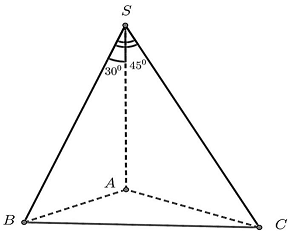
Theo giả thiết, $\vartriangle SAB$ vuông tại $A$ có $SB = a\sqrt 3 ,\widehat {ASB} = {30^ \circ }$. Khi đó, $SA = SB \cdot cos{30^ \circ } = \frac{{3a}}{2}$

và $AB = SB \cdot sin{30^ \circ } = \frac{{a\sqrt 3 }}{2}$.

Do $SA \bot \left( {ABC} \right)$ nên $\left( {SAB} \right) \bot \left( {ABC} \right)$. Vậy hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ cùng vuông góc

với $\left( {SAB} \right)$ nên suy ra $BC \bot \left( {SAB} \right) \Rightarrow \left( {SC,\left( {SAB} \right)} \right) = \left( {SC,SB} \right) = \widehat {CSB} = {45^ \circ }$.

Suy ra $\vartriangle SBC$ vuông cân tại $B \Rightarrow BC = SB = a\sqrt 3 $.

Mặt khác, $BC \bot \left( {SAB} \right) \Rightarrow CB \bot AB \Rightarrow \vartriangle ABC$ vuông tại $B$.

Khi đó, ${S_{\vartriangle ABC}} = \frac{1}{2}AB \cdot BC = \frac{{3{a^2}}}{4}$ và $V = \frac{1}{3}SA \cdot {S_{\vartriangle ABC}} = \frac{{3{a^3}}}{8}$.

Vậy tỉ số $\frac{{{a^3}}}{V} = \frac{8}{3}$.

a) Đúng: Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {ABC} \right)$.

b) Sai: Tam giác $SBC$ vuông cân tại $B$.

c) Đúng: Hai đường thẳng $AB$ và $CB$ vuông góc với nhau.

d) Sai: Nếu gọi thể tích khối chóp $S.ABC$ là $V$ thì tỷ số $\frac{{{a^3}}}{V}$ bằng $\frac{8}{3}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .

Câu 1: Có bao nhiêu giá trị nguyên của tham số $m \in \left( { – 2024;2024} \right)$ để hàm số $y = {\left( {{x^2} – 2x – m + 1} \right)^{\sqrt 7 }}$ có tập xác định là $\mathbb{R}$ ?

Lời giải

Hàm số $y = {\left( {{x^2} – 2x – m + 1} \right)^{\sqrt 7 }}$ có tập xác định là $\mathbb{R} \Leftrightarrow {x^2} – 2x – m + 1 > 0,\forall x \in \mathbb{R}$

$ \Leftrightarrow m < {(x + 1)^2},\forall x \in \mathbb{R}$

Mà $\left\{ {\begin{array}{*{20}{l}}
{m \in \mathbb{Z}} \\
{m \in \left( { – 2024;2024} \right)}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{m \in \mathbb{Z}} \\
{m \in \left( { – 2024;0} \right)}
\end{array}} \right.} \right.$ nên có 2023 giá trị $m$ thỏa mãn yêu cầu.

Câu 2: Tìm số nghiệm nguyên của bất phương trình ${log_{2 – \sqrt 3 }}\left( {x – 1} \right) + {log_{2 + \sqrt 3 }}\left( {11 – 2x} \right) \geqslant 0$.

Lời giải

Điều kiện $1 < x < \frac{{11}}{2}$.

Ta có ${log_{2 – \sqrt 3 }}\left( {x – 1} \right) + {log_{2 + \sqrt 3 }}\left( {11 – 2x} \right) \geqslant 0$

$ \Leftrightarrow {log_{2 – \sqrt 3 }}\left( {x – 1} \right) + {log_{2 – \sqrt 3 }}\frac{1}{{11 – 2x}} \geqslant 0$

$ \Leftrightarrow {log_{2 – \sqrt 3 }}\left( {\frac{{x – 1}}{{11 – 2x}}} \right) \geqslant 0 \Leftrightarrow \frac{{x – 1}}{{11 – 2x}} \leqslant 1$

$ \Leftrightarrow \frac{{3x – 12}}{{11 – 2x}} \leqslant 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x \leqslant 4} \\
{x > \frac{{11}}{2}}
\end{array}} \right.$

Kết hợp điều kiện suy ra $1 < x \leqslant 4$

Vậy bất phương trình có 3 nghiệm nguyên.

Câu 3: Số lượng của loại vi khuẩn $A$ trong một phòng thí nghiệm được tính theo công thức $S\left( t \right) = S\left( 0 \right) \cdot {2^t}$, trong đó $S\left( 0 \right)$ là số lượng vi khuẩn $A$ ban đầu, $S\left( t \right)$ là số lượng vi khuẩn $A$ có sau $t$ phút. Biết sau 3 phút thì số lượng vi khuẩn $A$ là 625 nghìn con. Hỏi sau bao lâu (đơn vị: phút) kể từ lúc ban đầu, số lượng vi khuẩn $A$ là 10 triệu con?

Lời giải

Vì sau 3 phút thì số lượng vi khuẩn $A$ là 625 nghìn con

Khi đó ta có: $625000 = S\left( 0 \right) \cdot {2^3} \Leftrightarrow S\left( 0 \right) = 78125$ con.

Thời gian để số lượng vi khuẩn $A$ là 10 triệu con là: $10000000 = {78125.2^t} \Leftrightarrow t = 7$ phút.

Câu 4: Cho hình chóp $S.ABC$ có $BC = a\sqrt 2 $ các cạnh còn lại đều bằng $a$. Tính góc giữa hai đường thẳng $SB$ và $AC$ (đơn vị: độ)

Lời giải

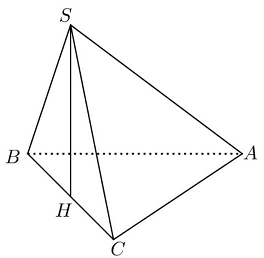
Gọi $\alpha = \overline {\left( {SB,AC} \right)} $. Do $A{B^2} + A{C^2} = B{C^2}$ nên tam giác $ABC$ vuông tại $A$.

Ta có $cos\alpha = \frac{{\left| {\overrightarrow {SB} \cdot \overrightarrow {AC} } \right|}}{{\left| {\overrightarrow {SB} \left| \cdot \right|\overrightarrow {AC} } \right|}} = \frac{{\left| {\left( {\overrightarrow {AB} – \overrightarrow {AS} } \right) \cdot \overrightarrow {AC} } \right|}}{{{a^2}}}$

$ = \frac{{\left| {\overrightarrow {AB} \cdot \overrightarrow {AC} – \overrightarrow {AS} \cdot \overrightarrow {AC} } \right|}}{{{a^2}}} = \frac{{\left| {\overrightarrow {AS} \cdot \overrightarrow {AC} } \right|}}{{{a^2}}}$

$ = \frac{{\left| {SA \cdot AC \cdot cos{{60}^ \circ }} \right|}}{{{a^2}}} = cos{60^ \circ }$.

Khi đó $\alpha = \widehat {\left( {SB,AC} \right)} = {60^ \circ }$

Câu 5: Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng 4 . Tính khoảng cách giữa hai đường thẳng $AB’$ và $CD’$

Lời giải

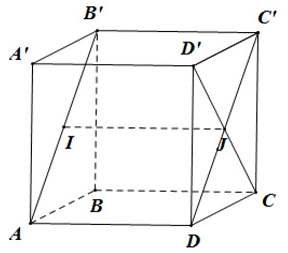
Gọi $I;J$ lần lượt là trung điểm của $AB’$ và $CD’$

Suy ra $J$ lần lượt là trung điểm của $DC’$. Do đó $IJ\parallel AD;IJ = AD = 2a$ (1)

Mặt khác $\left. {\begin{array}{*{20}{c}}
{AD \bot DD’} \\
{AD \bot DC}
\end{array}} \right\} \Rightarrow AD \bot \left( {DD’C’C} \right) \Rightarrow AD \bot CD’$

Tương tự $AD \bot AB’\left( 3 \right)$

Từ $\left( 1 \right),\left( 2 \right)$ và $\left( 3 \right)$ ta có: $IJ$ là đoạn vuông góc chung của 2 đường thẳng $AB’$ và $CD’$

Vậy khoảng cách giữa hai đường thẳng $AB’$ và $CD’$ bằng 4 .

Câu 6: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh 3 và đường chéo $AC = 3$. Tam giác $SAB$ cân tại $S$ và nằm trong mặt phẳng vuông góc với đáy. Góc giữa $\left( {SCD} \right)$ và đáy bằng ${45^ \circ }$. Tính thể tích của khối chóp $S.ABCD$ (đơn vị thể tích).

Lời giải

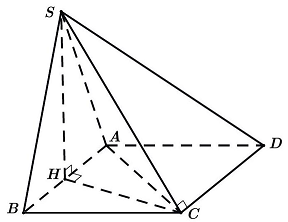
Ta có diện tích đáy ${S_{ABCD}} = 2{S_{\vartriangle ACD}} = \frac{{9\sqrt 3 }}{2}$.

Gọi $H$ là trung điểm $AB \Rightarrow SH \bot AB$, vì $\left\{ {\begin{array}{*{20}{l}}
{\left( {SAB} \right) \bot \left( {ABCD} \right)} \\
{\left( {SAB} \right) \cap \left( {ABCD} \right) = AB}
\end{array} \Rightarrow SH \bot \left( {ABCD} \right)} \right.$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{AB \bot SH} \\
{AB \bot CH\left( {doAB = BC = CA} \right)}
\end{array} \Rightarrow AB \bot \left( {SHC} \right)} \right.$, vì $CD//AB \Rightarrow CD \bot \left( {SHC} \right)$.

Ta lại có $\left\{ \begin{gathered}
(SCD) \cap (ABCD) = CD \hfill \\
SC \bot CD,\,SC \subset (SCD) \hfill \\
HC \bot CD,\,HC \subset (ABCD) \hfill \\
\end{gathered} \right.$

Suy ra, góc giữa $(SCD)$ và $(ABCD)$ là góc $\widehat {SCH}$

Suy ra $\vartriangle SHC$ vuông cân tại $H \Rightarrow SH = CH = \frac{{3\sqrt 3 }}{2}$.

Vậy $V = \frac{1}{3}{S_{ABCD}} \cdot SH = \frac{1}{3} \cdot \frac{{9\sqrt 3 }}{2} \cdot \frac{{3\sqrt 3 }}{2} = \frac{{{a^3}}}{4} = \frac{{27}}{4} = 6,75$ (đơn vị thể tích).