Đề Thi Giữa HK2 Toán 11 Cánh Diều Giải Chi Tiết-Đề 4

Đề thi giữa HK2 Toán 11 Cánh diều giải chi tiết-Đề 4 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.

Câu 1: Rút gọn biểu thức $P = {x^{\frac{1}{3}}} \cdot \sqrt[6]{x}$ với $x > 0$.

A. $P = {x^{\frac{1}{8}}}$. B. $P = {x^2}$. C. $P = {x^{\frac{2}{9}}}$. D. $P = \sqrt x $.

Câu 2: Gieo một đồng xu liên tiếp hai lần. Số phần tử của không gian mẫu $n\left( \Omega \right)$ là

A. 8 . B. 1 . C. 2 . D. 4 .

Câu 3: Mệnh đề nào sau đây là đúng?

A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.

C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.

Câu 4: Cho $A$ và $\overline A $ là hai biến cố đối nhau. Hãy chọn khẳng định đúng :

A. $P\left( A \right) = 1 + P\left( {\overline A } \right)$. B. $P\left( A \right) = P\left( {\overline A } \right)$. C. $P\left( A \right) = 1 – P\left( {\overline A } \right)$. D. $P\left( A \right) + P\left( {\overline A } \right) = 0$.

Câu 5: Nếu ${a^{\frac{1}{3}}} > {a^{\frac{1}{6}}}$ và ${b^{\sqrt 3 }} > {b^{\sqrt 5 }}$ thì

A. $a < 1;0 < b < 1$. B. $a > 1;b < 1$. C. $0 < a < 1;b < 1$ D. $a > 1;0 < b < 1$.

Câu 6: Tập xác định của hàm số $y = {(x – 1)^{ – 7}}$ là

A. $D = \left( {1; + \infty } \right)$. B. $D = \mathbb{R}$. C. $D = \mathbb{R} \setminus \left\{ 1 \right\}$. D. $D = \left[ {1; + \infty } \right)$.

Câu 7: Qua điểm $O$ cho trước có bao nhiêu mặt phẳng vuông góc với đường thẳng $\Delta $ cho trước

A. 1 . B. Vô số. C. 3 . D. 2 .

Câu 8: Cho các đồ thị hàm số $y = {a^x},y = {log_b}x,y = {x^c}$ ở hình vẽ sau đây.

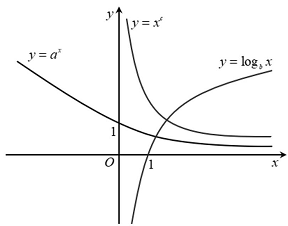
Khẳng định nào sau đây đúng?

A. $0 < c < 1 < a < b$. B. $c < 0 < a < 1 < b$. C. $c < 0 < a < b < 1$. D. $0 < c < a < b < 1$.

Câu 9: Viết biểu thức $P = \sqrt[3]{{x \cdot \sqrt[4]{x}}},(x > 0)$ dưới dạng lũy thừa với số mũ hữu tỷ

A. $P = {x^{\frac{5}{4}}}$. B. $P = {x^{\frac{1}{{12}}}}$. C. $P = {x^{\frac{1}{7}}}$. D. $P = {x^{\frac{5}{{12}}}}$.

Câu 10: Cho $a$ và $b$ là hai số thực dương thỏa mãn $a{b^2} = 9$. Giá trị của biểu thức ${log_3}a + 2{log_3}b$ bằng

A. 6 . B. 3 . C. 2 . D. 1 .

Câu 11: Cho $a,b > 0,a,b \ne 1$ và $x,y$ là hai số thực dương. Trong các mệnh đề dưới đây, mệnh đề nào sai?

A. ${log_a}\left( {xy} \right) = {log_a}x + {log_a}y$. B. ${log_b}a \cdot {log_a}x = {log_b}x$.

C. ${log_a}\left( {\frac{x}{y}} \right) = {log_a}x – {log_a}y$. D. ${log_a}\left( {\frac{1}{x}} \right) = \frac{1}{{{log_a}x}}$.

Câu 12: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $SA \bot \left( {ABCD} \right)$. Góc giữa đường thẳng $SD$ và mặt phẳng $\left( {ABCD} \right)$ là

A. $\widehat {ASD}$. B. $\widehat {DAS}$. C. $\widehat {SDA}$. D. $\widehat {SDC}$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Gọi $S$ là tập các số tự nhiên có bốn chữ số khác nhau được lập từ tập $E = \left\{ {1;2;3;4;5} \right\}$. Chọn ngẫu nhiên một số từ tập $S$.

a) Số các số tự nhiên có bốn chữ số khác nhau là 4 ! số.

b) Số phần tử của không gian mẫu là 120 phần tử.

c) Số các số tự nhiên chẵn có bốn chữ số khác nhau là 24 số

d) Xác xuất để số được chọn là một số chẵn bằng 0,4 .

Câu 2: Cho hình chóp $S.ABCD$ có $SA = AB\sqrt 3 $ và $SA \bot \left( {ABCD} \right),ABCD$ là tứ giác nội tiếp đường

tròn đường kính $AC,\widehat {ACB} = {60^ \circ }$. Gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ trên $SB$ và $SD$.

a) Góc giữa hai đường thẳng $SA$ và $SC$ bằng góc giữa hai mặt phẳng $\left( {AHK} \right)$ và $\left( {ABCD} \right)$.

b) Đường thẳng $SC$ vuông góc với mặt phẳng $\left( {AHK} \right)$

c) Góc giữa hai đường thẳng $SA$ và $SC$ bằng ${45^ \circ }$

d) Tính tan của góc hợp bởi mặt phẳng $\left( {AHK} \right)$ và mặt phẳng $\left( {ABCD} \right)$ bằng $\frac{2}{3}$

Câu 3: Cho các hàm số $y = {log_a}x,y = {a^x}$ với $a$ là số thực dương khác 1 . Xét tính đúng sai của các mệnh đề sau:

a) Đồ thị hàm số $y = {a^x}$ và đồ thị hàm số $y = {log_a}x$ đối xứng nhau qua đường thẳng $y = x$.

b) Hàm số $y = {log_a}x$ và hàm số $y = {a^x}$ có cùng tập giá trị.

c) Hàm số $y = {a^x}$ với $0 < a < 1$ nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right)$.

d) Đồ thị hàm số $y = {a^x}$ với $a > 0$ và $a \ne 1$ luôn đi qua điểm $A\left( {a;1} \right)$.

Câu 4: Cho hình chóp $S \cdot ABCD$, đáy $ABCD$ là hình vuông cạnh $a,SA$ vuông góc với đáy. Gọi $O$ là giao điể của $AC$ và $BD$. Kẻ $OH \bot SC$ với $H \in SC$. Khoảng cách giữa hai đường thẳng $BD$ và $SC$ là $\frac{a}{2}$. Tính thể tích khối chóp $S \cdot ABCD$.

a) Đường thẳng $BD$ vuông góc với mặt phẳng $\left( {SAC} \right)$

b) Độ dài đoạn vuông góc chung của $BD$ và $SC$ bằng $2a$.

c) Chiều cao của khối chóp $S.ABCD$ bằng $2a\sqrt 2 $

d) Thể tích khối chóp $S.ABCD$ bằng $\frac{{{a^2}\sqrt 2 }}{3}$

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả như bảng sau. Hỏi trong năm 2023, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?

Số cuốn sách	3	4	5	6	7
Số bạn	6	15	3	8	8

Câu 2: Chọn ngẫu nhiên hai số khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn là

Câu 3: Cho $x,y$ là hai số nguyên thỏa mãn: ${3^x} \cdot {6^y} = \frac{{{2^{15}} \cdot {6^{40}}}}{{{9^{50}} \cdot {{12}^{25}}}}$. Tính $xy$ ?

Câu 4: Ông An gửi 200 triệu đồng vào ngân hàng theo hình thức lãi kép theo kì hạn năm, với lãi suất là $6,5\%$ một năm và lãi suất không đổi trong thời gian gửi. Sau 6 năm, số tiền lãi ( làm tròn đến hàng triệu ) của ông là bao nhiêu?

Câu 5: Chọn ngẫu nhiên 3 số trong 20 số nguyên dương đầu tiên. Biết xác suất để trong 3 số được chọn có ít nhất 1 số chẵn bằng $\frac{a}{b}$ với $a,b$ là các số nguyên tố. Tổng $a + b$ bằng bao nhiêu?

Câu 6: Cho lăng trụ đứng $ABC \cdot A’B’C’$ có đáy là tam giác $ABC$ là tam giác vuông cân tại $A$, cạnh $BC = 1$. Gọi $M$ là trung điểm của cạnh $AA’$, biết hai mặt phẳng $\left( {MBC} \right)$ và $\left( {MB’C’} \right)$ vuông góc với nhau. Tính thể tích khối lăng trụ $ABC \cdot A’B’C’$.

ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phương án.

Câu 1: Rút gọn biểu thức $P = {x^{\frac{1}{3}}} \cdot \sqrt[6]{x}$ với $x > 0$.

A. $P = {x^{\frac{1}{8}}}$.

B. $P = {x^2}$.

C. $P = {x^{\frac{2}{9}}}$.

D. $P = \sqrt x $.

Lời giải

Với $x > 0$, ta có $P = {x^{\frac{1}{3}}} \cdot \sqrt[6]{x} = {x^{\frac{1}{3}}} \cdot {x^{\frac{1}{6}}} = {x^{\frac{1}{3} + \frac{1}{6}}} = {x^{\frac{1}{2}}} = \sqrt x $.

Câu 2: Gieo một đồng xu liên tiếp hai lần. Số phần tử của không gian mẫu $n\left( \Omega \right)$ là

A. 8 .

B. 1 .

C. 2 .

D. 4 .

Lời giải

Số phần tử của không gian mẫu $n\left( \Omega \right) = 2.2 = 4$.

Câu 3: Mệnh đề nào sau đây là đúng?

A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.

C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.

Lời giải

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.

Câu 4: Cho $A$ và $\overline A $ là hai biến cố đối nhau. Hãy chọn khẳng định đúng :

A. $P\left( A \right) = 1 + P\left( {\overline A } \right)$.

B. $P\left( A \right) = P\left( {\overline A } \right)$.

C. $P\left( A \right) = 1 – P\left( {\overline A } \right)$.

D. $P\left( A \right) + P\left( {\overline A } \right) = 0$.

Lời giải

Vì $A \cup \overline A = \Omega $ và $A \cap \overline A = \emptyset $. Nên $P\left( A \right) + P\left( {\overline A } \right) = 1 \Leftrightarrow P\left( A \right) = 1 – P\left( {\overline A } \right)$.

Câu 5: Nếu ${a^{\frac{1}{3}}} > {a^{\frac{1}{6}}}$ và ${b^{\sqrt 3 }} > {b^{\sqrt 5 }}$ thì

A. $a < 1;0 < b < 1$.

B. $a > 1;b < 1$.

C. $0 < a < 1;b < 1$

D. $a > 1;0 < b < 1$.

Lời giải

Ta có: $\frac{1}{3} > \frac{1}{6}$, lại có ${a^{\frac{1}{3}}} > {a^{\frac{1}{6}}} \Rightarrow a > 1$.

Ta có: $\sqrt 3 < \sqrt 5 $, lại có ${b^{\sqrt 3 }} > {b^{\sqrt 5 }} \Rightarrow 0 < b < 1$.

Câu 6: Tập xác định của hàm số $y = {(x – 1)^{ – 7}}$ là

A. $D = \left( {1; + \infty } \right)$.

B. $D = \mathbb{R}$.

C. $D = \mathbb{R} \setminus \left\{ 1 \right\}$.

D. $D = \left[ {1; + \infty } \right)$.

Lời giải

Điều kiện $x – 1 \ne 0 \Leftrightarrow x \ne 1$. Vậy $D = \mathbb{R} \setminus \left\{ 1 \right\}$.

Câu 7: Qua điểm $O$ cho trước có bao nhiêu mặt phẳng vuông góc với đường thẳng $\Delta $ cho trước

A. 1 .

B. Vô số.

C. 3 .

D. 2 .

Lời giải

Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Câu 8: Cho các đồ thị hàm số $y = {a^x},y = {log_b}x,y = {x^c}$ ở hình vẽ sau đây.

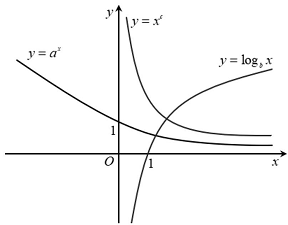
Khẳng định nào sau đây đúng?

A. $0 < c < 1 < a < b$.

B. $c < 0 < a < 1 < b$.

C. $c < 0 < a < b < 1$.

D. $0 < c < a < b < 1$.

Lời giải

Ta thấy đồ thị $y = {x^c}$ đi xuống nên $c < 0$, đồ thị $y = {a^x}$ đi xuống nên $0 < a < 1$, đồ thị $y = {log_b}x$ đi lên nên $b > 1$.

Câu 9: Viết biểu thức $P = \sqrt[3]{{x \cdot \sqrt[4]{x}}},(x > 0)$ dưới dạng lũy thừa với số mũ hữu tỷ

A. $P = {x^{\frac{5}{4}}}$.

B. $P = {x^{\frac{1}{{12}}}}$.

C. $P = {x^{\frac{1}{7}}}$.

D. $P = {x^{\frac{5}{{12}}}}$.

Lời giải

Ta có $P = \sqrt[3]{{x \cdot \sqrt[4]{x}}} = \sqrt[3]{{x \cdot {x^{\frac{1}{4}}}}} = \sqrt[3]{{{x^{\frac{5}{4}}}}} = {x^{\frac{5}{{12}}}}$.

Câu 10: Cho $a$ và $b$ là hai số thực dương thỏa mãn $a{b^2} = 9$. Giá trị của biểu thức ${log_3}a + 2{log_3}b$ bằng

A. 6 .

B. 3 .

C. 2 .

D. 1 .

Lời giải

Ta có $a{b^2} = 9 \Rightarrow {log_3}\left( {a{b^2}} \right) = {log_3}9 \Rightarrow {log_3}a + 2{log_2}b = 2$.

Câu 11: Cho $a,b > 0,a,b \ne 1$ và $x,y$ là hai số thực dương. Trong các mệnh đề dưới đây, mệnh đề nào sai?

A. ${log_a}\left( {xy} \right) = {log_a}x + {log_a}y$.

B. ${log_b}a \cdot {log_a}x = {log_b}x$.

C. ${log_a}\left( {\frac{x}{y}} \right) = {log_a}x – {log_a}y$.

D. ${log_a}\left( {\frac{1}{x}} \right) = \frac{1}{{{log_a}x}}$.

Lời giải

Ta có ${log_a}\left( {\frac{1}{x}} \right) = – {log_a}x$ nên ${log_a}\left( {\frac{1}{x}} \right) = \frac{1}{{{log_a}x}}$ là sai.

Câu 12: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $SA \bot \left( {ABCD} \right)$. Góc giữa đường thẳng $SD$ và mặt phẳng $\left( {ABCD} \right)$ là

A. $\widehat {ASD}$.

B. $\widehat {DAS}$.

C. $\widehat {SDA}$.

D. $\widehat {SDC}$.

Lời giải

Hình chiếu của $SD$ lên $mp (ABCD)$ là $AD$ nên góc giữa $SD$ và mặt phẳng $(ABCD)$ là góc $\widehat {SDA}$

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Gọi $S$ là tập các số tự nhiên có bốn chữ số khác nhau được lập từ tập $E = \left\{ {1;2;3;4;5} \right\}$. Chọn ngẫu nhiên một số từ tập $S$.

a) Số các số tự nhiên có bốn chữ số khác nhau là 4! số.

b) Số phần tử của không gian mẫu là 120 phần tử.

c) Số các số tự nhiên chẵn có bốn chữ số khác nhau là 24 số

d) Xác xuất để số được chọn là một số chẵn bằng 0,4 .

Lời giải

Gọi $A$ là biến cố “số được chọn là một số chẵn”

Số các số tự nhiên có bốn chữ số khác nhau là $A_5^4 = 120$

Số phần tử của không gian mẫu $n\left( \Omega \right) = C_{120}^1 = 120$

Số các số tự nhiên chẵn có bốn chữ số khác nhau $2A_4^3 = 48$

Số kết quả thuận lợi của biến cố $A$ là $n\left( A \right) = C_{48}^1 = 48$

Vậy xác xuất để số được chọn là một số chẵn là $P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{48}}{{120}} = \frac{2}{5}$.

a) Sai: Số các số tự nhiên có bốn chữ số khác nhau là $A_5^4 = 120$ số.

b) Đúng: Số phần tử của không gian mẫu là 120 phần tử.

c) Sai: Số các số tự nhiên chẵn có bốn chữ số khác nhau là $2A_4^3 = 48$ số

d) Đúng: Xác xuất để số được chọn là một số chẵn bằng 0,4 .

Câu 2: Cho hình chóp $S.ABCD$ có $SA = AB\sqrt 3 $ và $SA \bot \left( {ABCD} \right),ABCD$ là tứ giác nội tiếp đường tròn đường kính $AC,\widehat {ACB} = {60^ \circ }$. Gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ trên $SB$ và $SD$.

a) Góc giữa hai đường thẳng $SA$ và $SC$ bằng góc giữa hai mặt phẳng $\left( {AHK} \right)$ và $\left( {ABCD} \right)$

b) Đường thẳng $SC$ vuông góc với mặt phẳng $\left( {AHK} \right)$

c) Góc giữa hai đường thẳng $SA$ và $SC$ bằng ${45^ \circ }$

d) Tính tan của góc hợp bởi mặt phẳng $\left( {AHK} \right)$ và mặt phẳng $\left( {ABCD} \right)$ bằng $\frac{2}{3}$

Lời giải

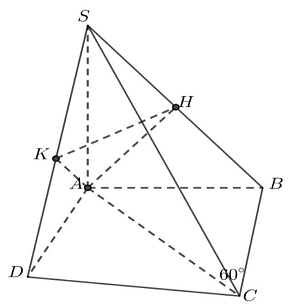
Từ giả thiết: $ABCD$ là tứ giác nội tiếp đường tròn đường kính $AC$ nên tam giác $ABC$ vuông tại $B$ và tam giác $ADC$ vuông tại $D$, do đó $AB \bot BC,AD \bot DC$.

Nhận thấy: $AH \bot SB$, mà $AH \bot BC$ (do $BC \bot AB,BC \bot SA \Rightarrow BC \bot \left( {SAB} \right)$ )

$ \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$

Lại có: $AK \bot SD$, mà $AK \bot CD$ (do $CD \bot AD,CD \bot SA \Rightarrow CD \bot \left( {SAD} \right)$ )

$ \Rightarrow AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC$

Từ (1),(2) suy ra $SC \bot \left( {AHK} \right)$ mà $SA \bot \left( {ABCD} \right)$

Ta được góc giữa hai mặt phẳng $\left( {AHK} \right)$ và $\left( {ABCD} \right)$ là góc giữa hai đường thẳng $SA,SC$.

$ \Rightarrow \left( {\widehat {\left( {AHK} \right);\left( {ABCD} \right)}} \right) = \widehat {ASC}$

Ta có: $tan\widehat {ASC} = \frac{{AC}}{{AS}} = \frac{{\frac{{AB}}{{sin{{60}^ \circ }}}}}{{AB\sqrt 3 }} = \frac{{\frac{{AB}}{{\sqrt 3 }}}}{{AB\sqrt 3 }} = \frac{2}{{\sqrt 3 }} \cdot \frac{1}{{\sqrt 3 }} = \frac{2}{3}$.

a) Đúng: Góc giữa hai đường thẳng $SA$ và $SC$ bằng góc giữa hai mặt phẳng $\left( {AHK} \right)$ và $\left( {ABCD} \right)$

b) Đúng: Đường thẳng $SC$ vuông góc với mặt phẳng $\left( {AHK} \right)$

c) Sai: Góc giữa hai đường thẳng $SA$ và $SC$ bằng $arctan\left( {\frac{2}{3}} \right) \approx {33^ \circ }$

d) Đúng: Tính tan của góc hợp bởi mặt phẳng $\left( {AHK} \right)$ và mặt phẳng $\left( {ABCD} \right)$ bằng $\frac{2}{3}$

Câu 3: Cho các hàm số $y = {log_a}x,y = {a^x}$ với $a$ là số thực dương khác 1 . Xét tính đúng sai của các mệnh đề sau:

a) Đồ thị hàm số $y = {a^x}$ và đồ thị hàm số $y = {log_a}x$ đối xứng nhau qua đường thẳng $y = x$.

b) Hàm số $y = {log_a}x$ và hàm số $y = {a^x}$ có cùng tập giá trị.

c) Hàm số $y = {a^x}$ với $0 < a < 1$ nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right)$.

d) Đồ thị hàm số $y = {a^x}$ với $a > 0$ và $a \ne 1$ luôn đi qua điểm $A\left( {a;1} \right)$.

Lời giải

a) Đúng: Đồ thị hàm số $y = {a^x}$ và đồ thị hàm số $y = {log_a}x$ đối xứng nhau qua đường thẳng $y = x$

b) Sai: Hàm số $y = {log_a}x$ có tập giá trị là $\mathbb{R}$ và hàm số $y = {a^x}$ có tập giá trị là $\left( {0; + \infty } \right)$.

c) Đúng: Hàm số $y = {a^x}$ với $0 < a < 1$ nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right)$.

d) Sai: Đồ thị hàm số $y = {a^x}$ với $a > 0$ và $a \ne 1$ luôn đi qua điểm $A\left( {a;{a^a}} \right)$ hoặc $A\left( {0;1} \right)$.

Câu 4: Cho hình chóp $S.ABCD$, đáy $ABCD$ là hình vuông cạnh $a,SA$ vuông góc với đáy. Gọi $O$ là giao điể của $AC$ và $BD$. Kẻ $OH \bot SC$ với $H \in SC$. Khoảng cách giữa hai đường thẳng $BD$ và $SC$ là $\frac{a}{2}$. Tính thể tích khối chóp $S.ABCD$.

a) Đường thẳng $BD$ vuông góc với mặt phẳng $\left( {SAC} \right)$

b) Độ dài đoạn vuông góc chung của $BD$ và $SC$ bằng $2a$

c) Chiều cao của khối chóp $S.ABCD$ bằng $2a\sqrt 2 $

d) Thể tích khối chóp $S.ABCD$ bằng $\frac{{{a^2}\sqrt 2 }}{3}$

Lời giải

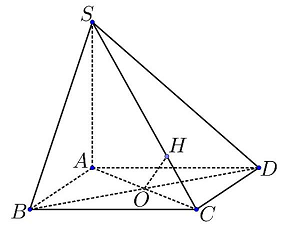
Theo giả thiết : $OH \bot SC\left( {H \in SC} \right)$ (1).

Ta có $\left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot OH} \right.$ (2).

Từ (1) và (2) ta có $OH$ là đoạn vuông góc chung của $BD$ và $SC$.

Vậy $d\left( {BD,SC} \right) = OH = \frac{a}{2}$.

Xét hai tam giác đồng dạng $CHO$ và $CAS$ ta có:

$\frac{{OH}}{{SA}} = \frac{{CO}}{{SC}} \Leftrightarrow \frac{{\frac{a}{2}}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\sqrt {S{A^2} + 2{a^2}} }} \Leftrightarrow SA = a\sqrt 2 .$

Vậy ${V_{S.ABCD}} = \frac{1}{3} \cdot SA \cdot {S_{ABCD}} = \frac{1}{3} \cdot a\sqrt 2 \cdot {a^2} = \frac{{{a^3}\sqrt 2 }}{3}$.

a) Đúng: Đường thẳng $BD$ vuông góc với mặt phẳng $\left( {SAC} \right)$

b) Sai: Độ dài đoạn vuông góc chung của $BD$ và $SC$ bằng $\frac{a}{2}$.

c) Sai: Chiều cao của khối chóp $S.ABCD$ bằng $a\sqrt 2 $

d) Sai: Thể tích khối chóp $S.ABCD$ bằng $\frac{{{a^3}\sqrt 2 }}{3}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .

Câu 1: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2023, bạn Lan thu được kết quả như bảng sau. Hỏi trong năm 2023, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?

Số cuốn sách	3	4	5	6	7
Số bạn	6	15	3	8	8

Lời giải

Số bạn học sinh trong lớp là $n = 6 + 15 + 3 + 8 + 8 = 40$ (bạn)

Trong năm 2023, trung bình mỗi bạn trong lớp đọc số cuốn sách là:

$\overline x = \frac{{6.3 + 15.4 + 3.5 + 8.6 + 8.7}}{{40}} = 4,925$

Câu 2: Chọn ngẫu nhiên hai số khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn là

Lời giải

Số cách chọn hai số khác nhau từ 25 số nguyên dương đầu tiên là $C_{25}^2 = 300 \Rightarrow n\left( \Omega \right) = 300$.

Gọi $A$ là biến cố “Tổng hai số được chọn là một số chẵn”.

Ta có hai trường hợp

Trường hợp 1: Chọn 2 số chẵn khác nhau từ tập 12 số chẵn có $C_{12}^2 = 66$ cách.

Trường hợp 2: Chọn 2 số lẻ khác nhau từ tập 13 số lẻ có $C_{13}^2 = 78$ cách.

Do đó $n\left( A \right) = 66 + 78 = 144$.

Vậy xác suất cần tìm là $P\left( A \right) = \frac{{144}}{{300}} = \frac{{12}}{{25}} = 0,48$.

Câu 3: Cho $x,y$ là hai số nguyên thỏa mãn: ${3^x} \cdot {6^y} = \frac{{{2^{15}} \cdot {6^{40}}}}{{{9^{50}} \cdot {{12}^{25}}}}$. Tính $xy$ ?

Lời giải

Ta có: ${3^x} \cdot {6^y} = \frac{{{2^{15}} \cdot {6^{40}}}}{{{9^{50}} \cdot {{12}^{25}}}} \Leftrightarrow {3^x} \cdot {3^y} \cdot {2^y} = \frac{{{2^{15}} \cdot {2^{40}} \cdot {3^{40}}}}{{{3^{100}} \cdot {3^{25}} \cdot {2^{50}}}} \Leftrightarrow {3^{x + y}} \cdot {2^y} = {3^{ – 85}} \cdot {2^5}$

$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{x + y = – 85} \\
{y = 5}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x = – 90} \\
{y = 5}
\end{array} \Rightarrow xy = – 450} \right.} \right.$

Vậy $xy = – 450$.

Câu 4: Ông An gửi 200 triệu đồng vào ngân hàng theo hình thức lãi kép theo kì hạn năm, với lãi suất là $6,5\%$ một năm và lãi suất không đổi trong thời gian gửi. Sau 6 năm, số tiền lãi ( làm tròn đến hàng triệu ) của ông là

Lời giải

Đặt số tiền gốc của ông An là: $A = 200$ triệu.

Hết năm thứ nhất, số tiền cả gốc và lãi ông An nhận được là: ${A_1} = 200\left( {1 + 6,5\%} \right)$ triệu.

Hết năm thứ hai, số tiền cả gốc và lãi ông An nhận được là: ${A_2} = 200{(1 + 6,5\%)^2}$ triệu.

Hết năm thứ sáu, số tiền cả gốc và lãi ông An nhận được là: ${A_6} = 200{(1 + 6,5\%)^6}$ triệu.

Vậy sau 6 năm số tiền lãi ông An nhận được là: ${A_6} – A \approx 92$ triệu.

Câu 5: Chọn ngẫu nhiên 3 số trong 20 số nguyên dương đầu tiên. Biết xác suất để trong 3 số được

chọn có ít nhất 1 số chẵn bằng $\frac{a}{b}$ với $a,b$ là các số nguyên tố. Tổng $a + b$ bằng bao nhiêu?

Lời giải

Trong 20 số nguyên dương đầu tiên có 10 số chẵn và 10 số lẻ.

Số cách chọn ngẫu nhiên 3 số trong 20 số nguyên dương đầu tiên là $n\left( \Omega \right) = C_{20}^3$.

Xét biến cố $A$ : ” Chọn 3 số trong đó có ít nhất 1 số chẵn”.

Xét biến cố đối của biến cố $A$ là biến cố $\overline A $ : “ Chọn 3 số đều là các số lẻ”.

Ta có $n\left( {\overline A } \right) = C_{10}^3$, do đó xác suất để chọn được 3 số đều lẻ là $P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^3}}{{C_{20}^3}} = \frac{2}{{19}}$.

Vậy xác suất để chọn được 3 số trong đó có ít nhất 1 số chẵn là:

$P\left( A \right) = 1 – P\left( {\overline A } \right) = 1 – \frac{2}{{19}} = \frac{{17}}{{19}}$.

Ta có $a = 17;b = 19$ do đó $a + b = 36$.

Câu 6: Cho lăng trụ đứng $ABC \cdot A’B’C’$ có đáy là tam giác $ABC$ là tam giác vuông cân tại $A$, cạnh $BC = 1$. Gọi $M$ là trung điểm của cạnh $AA’$, biết hai mặt phẳng $\left( {MBC} \right)$ và $\left( {MB’C’} \right)$ vuông góc với nhau. Tính thể tích khối lăng trụ $ABC \cdot A’B’C’$.

Lời giải

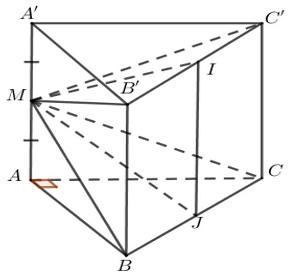
Đặt $AA’ = h$.

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{M \in \left( {MBC} \right) \cap \left( {MB’C’} \right)} \\
{BC \subset \left( {MBC} \right);B’C’ \subset \left( {MB’C’} \right)\;} \\
{BC//B’C’}
\end{array}} \right.$

$ \Rightarrow \left( {MBC} \right) \cap \left( {MB’C’} \right) = \Delta ,$với $\Delta \;$qua $M$và $\Delta //BC//B’C’$.

Gọi $I,J$ lần lượt là trung điểm của $BC$ và $B’C’$, khi đó $MI \bot BC,MJ \bot B’C’$ (vì các tam giác $MBC$ và $MB’C’$ cân tại $M$ ) hay $MI \bot \Delta $ hay $MJ \bot \Delta $.

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{\left( {MBC} \right) \cap \left( {MB’C’} \right) = \Delta } \\
{MI \subset \left( {MBC} \right),MI \bot \Delta } \\
{MJ \subset \left( {MB’C’} \right),MJ \bot \Delta }
\end{array}} \right.$

$ \Rightarrow \left( {\left( {MBC} \right);\left( {MB’C’} \right)} \right) = \left( {MI;MJ} \right) = {90^ \circ }$.

Ta có $:AB = AC = \frac{a}{{\sqrt 2 }};AI = \frac{1}{2};MI = MJ = \sqrt {M{A^2} + A{I^2}} = \sqrt {\frac{{{h^2}}}{4} + \frac{1}{4}} $.

Xét tam giác $MIJ$ vuông cân tại $M$ có: $I{J^2} = 2M{I^2} \Leftrightarrow {h^2} = \frac{{{h^2}}}{2} + \frac{1}{2} \Rightarrow h = 1$.

Thể tích khối lăng trụ $ABC \cdot A’B’C’$ là :

${V_{ABC \cdot A’B’C’}} = {S_{ABC}} \cdot AA’ = \frac{1}{2} \cdot AB \cdot AC \cdot AA’ = \frac{1}{2} \cdot \frac{1}{{\sqrt 2 }} \cdot \frac{1}{{\sqrt 2 }} \cdot 1 = \frac{1}{4} = 0,25$.