Đề Thi Giữa HK 2 Toán 11 Cánh Diều Giải Chi Tiết-Đề 5

Đề thi giữa HK 2 Toán 11 Cánh diều giải chi tiết-Đề 5 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Một tổ có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 2 học sinh. Tính xác suất sao cho 2 học sinh được chọn đều là nữ.

A. $\frac{1}{5}$. B. $\frac{1}{{15}}$. C. $\frac{7}{{15}}$. D. $\frac{8}{{15}}$.

Câu 2: Một nhóm học sinh gồm 10 học sinh nam và 5 học sinh nũ̃. Giáo viên chọn ngẫu nhiên một học sinh đi lên bảng làm bài tập. Tính xác suất chọn được một học sinh nữ?

A. $\frac{1}{2}$. B. $\frac{1}{{10}}$. C. $\frac{1}{5}$. D. $\frac{1}{3}$.

Câu 3: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Góc giữa hai đường thẳng $AA’$ và $BD$ bằng bao nhiêu độ?

A. ${30^ \circ }$. B. ${60^ \circ }$. C. ${45^ \circ }$. D. ${90^ \circ }$.

Câu 4: Trong không gian cho hai đường thẳng phân biệt $a;b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Mệnh đề nào sau đây sai?

A. Nếu $b\parallel a$ thì $b \bot \left( P \right)$. B. Nếu $b \bot a$ thì $b\parallel \left( P \right)$.

C. Nếu $b\parallel \left( P \right)$ thì $b \bot a$. D. Nếu $b \bot \left( P \right)$ thì $b\parallel a$.

Câu 5: Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc mặt đáy $\left( {ABC} \right)$. Góc tạo bởi $SB$ và đáy tương ứng là:

A. $\widehat {SCA}$ B. $\widehat {SBA}$. C. $\widehat {SBC}$. D. $\widehat {SAB}$.

Câu 6: Với $a$ là số thực dương tùy ý, $\sqrt[3]{{{a^2}}}$ bằng:

A. ${a^{\frac{1}{6}}}$. B. ${a^6}$. C. ${a^{\frac{2}{3}}}$. D. ${a^{\frac{3}{2}}}$.

Câu 7: Với $x$ là số thực dương bất kỳ, biểu thức $P = \sqrt[3]{{\sqrt x }}$ bằng

A. ${x^{\frac{2}{3}}}$. B. ${x^{\frac{5}{6}}}$. C. ${x^{\frac{1}{6}}}$. D. ${x^{\frac{3}{2}}}$.

Câu 8: Cho $a,b > 0$ thỏa mãn ${a^{\frac{2}{3}}} > {a^{\frac{1}{2}}},{b^{\frac{2}{3}}} > {b^{\frac{3}{4}}}$. Khi đó khẳng định nào sau đây đúng?

A. $0 < a\left\langle {1,b} \right\rangle 1$. B. $a > 1,0 < b < 1$. C. $a > 1,b > 1$. D. $0 < a < 1,0 < b < 1$.

Câu 9: Cho $a,b$ là các số thực dương, $a \ne 1$ thỏa mãn ${log_a}b = 3$. Tính ${log_{\sqrt a }}{a^2}{b^3}$ ?

A. 24 . B. 25 . C. 22 . D. 23 .

Câu 10: Tập xác định của hàm số $y = {(x – 1)^{\sqrt 3 }}$ là

A. $\mathbb{R} \setminus \left\{ 1 \right\}$. B. $\mathbb{R}$. C. $\left( {1; + \infty } \right)$. D. $\left( { – 1; + \infty } \right)$.

Câu 11: Đường cong trong hình bên là của đồ thị hàm số nào sau đây?

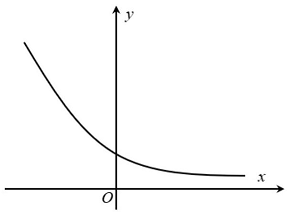
A. $y = {log_2}x$. B. $y = {(0,8)^x}$. C. $y = {log_{0,4}}x$. D. $y = {(\sqrt 2 )^x}$.

Câu 12: Trong các khẳng định sau, khẳng định nào sai?

A. ${log_{{a^2} + 4}}\left( {{a^2} + 1} \right) \geqslant 0\forall a$. B. ${4^{ – \sqrt 3 }} < {4^{ – \sqrt 2 }}$. C. ${2^{30}} < {3^{20}}$. D. $0,{99^\pi } > 0,{99^e}$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Giả sử $A,B$ là hai điểm phân biệt trên đồ thị của hàm số $y = {log_3}\left( {5x – 3} \right)$ sao cho $A$ là trung điểm của đoạn $OB$.

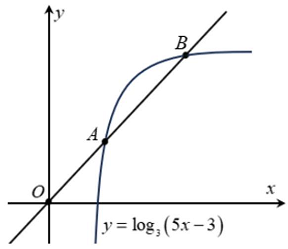
a) Hoành độ của điểm $B$ là một số nguyên.

b) Trung điểm của đoạn thẳng $OB$ có tọa độ $\left( {\frac{{12}}{5};1} \right)$.

c) Gọi $H$ là hình chiếu của điểm $B$ xuống trục hoành. Khi đó ${S_{\vartriangle OBH}} = \frac{{\sqrt {61} }}{{25}}$

d) Đoạn thẳng $AB$ có độ dài bằng $\frac{{\sqrt {61} }}{5}$.

Câu 2: Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B,AB = BC = a$. Cạnh bên $SA$ vuông góc với mặt phẳng đáy $\left( {ABC} \right)$ và $SA = a$. Gọi $I$ là trung điểm của $AC$ và kẻ $IH \bot SC$.

a) Đường thẳng $SC$ vuông góc với mặt phẳng $\left( {BHI} \right)$

b) Cosin góc tạo bởi hai đường thẳng $IH$ và $BH$ bằng $\frac{{\sqrt 3 }}{2}$.

c) Độ dài đoạn thẳng $BH$ bằng $\frac{{a\sqrt 2 }}{2}$

d) Góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBC} \right)$ bằng ${60^ \circ }$.

Câu 3: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

a) Tổng số học sinh được khảo sát là 42 học sinh.

b) Giá trị đại diện của nhóm $\left[ {20;40} \right)$ là 25 .

c) Số trung bình của mẫu số liệu trên thuộc nhóm $\left[ {0;20} \right)$.

d) Có 16 học sinh tập thể dục ít nhất 1 giờ trong ngày.

Câu 4: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Biết $SA = a\sqrt 2 $ và $SA$ vuông góc với mặt đáy. Gọi $M$ là trung điểm của $BC$ và $H$ là hình chiếu vuông góc của $A$ lên $SM$.

a) Đường thẳng $AH$ vuông góc với mặt phẳng $\left( {SBC} \right)$.

b) Đường thẳng $SH$ là hình chiếu của đường thẳng $SA$ lên mặt phẳng $\left( {SBC} \right)$

c) Độ dài đoạn thẳng $AH$ bằng $\frac{{6a}}{{11}}$

d) Cosin góc tạo bởi đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ bằng $\frac{{\sqrt {11} }}{{33}}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Tứ phân vị thứ nhất ${Q_1}$ của mẫu số liệu ghép nhóm này (Kết quả làm tròn đến hàng trăm)

Câu 2: Cho tập $A = \left\{ {0;1;2;3;4;5} \right\}$. Gọi $S$ là tập các số tự nhiên có 5 chữ số khác nhau lập từ $A$. Lấy từ $S$ một phần tử, tính xác suất để số lấy được là một số chia hết cho 5 .

Câu 3: Mức sản xuất của một hãng DVD trong một ngày là $q\left( {m,n} \right) = {m^{\frac{2}{3}}}{n^{\frac{1}{3}}}$. Trong đó $m$ là số lượng nhân viên và $n$ là số lao động chính. Mỗi ngày hãng phải sản xuất 40 sản phẩm để đáp ứng nhu cầu của khách hàng. Biết rằng lương của nhân viên là $16\$ $ / ngày và lương của lao động chính là $27\$ $/ngày. Giá trị nhỏ nhất chi phí một ngày của hãng sản xuất này là bao nhiêu $\$ $ ?

Câu 4: Một chiếc máy có hai động cơ $I$ và $II$ chạy độc lập nhau. Xác suất để động cơ $I$ và $II$ chạy tốt lần lượt là 0,8 và 0,7 . Tính xác suất để ít nhất một động cơ chạy tốt

Câu 5: Năm 2020 , một hãng xe ô tô niêm yết giá bán loại xe $X$ là 850.000 .000 đồng và dự định trong 10 năm tiếp theo, mỗi năm giảm $2\% $ giá bán so với giá bán của năm liền trước. Theo dự định đó, năm 2025 hãng xe ô tô niêm yết giá bán loại xe $X$ là bao nhiêu (đơn vị: triệu đồng) (Kết quả làm tròn đến hàng đơn vị)?

Câu 6: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$, cạnh bên $SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 ,AD = 2AB = 2BC = 2a$. Tính côsin của góc giữa 2 mặt phẳng $\left( {SAD} \right)$ và $\left( {SCD} \right)$.

ĐÁP ÁN VÀ HƯỚNG DÃ̃N GIẢI CHI TIẾT

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án.

Câu 1: Một tổ có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 2 học sinh. Tính xác suất sao cho 2 học sinh được chọn đều là nữ.

A. $\frac{1}{5}$.

B. $\frac{1}{{15}}$.

C. $\frac{7}{{15}}$.

D. $\frac{8}{{15}}$.

Lời giải

Xác suất 2 học sinh được chọn đều là nữ là $\frac{{C_3^2}}{{C_{10}^2}} = \frac{1}{{15}}$.

Câu 2: Một nhóm học sinh gồm 10 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên một học sinh đi lên bảng làm bài tập. Tính xác suất chọn được một học sinh nữ?

A. $\frac{1}{2}$.

B. $\frac{1}{{10}}$.

C. $\frac{1}{5}$.

D. $\frac{1}{3}$.

Lời giải

Có 15 cách chọn một học sinh trong nhóm.

Có 5 cách chọn một học sinh nữ.

Xác suất để chọn được một học sinh nữ là: $\frac{5}{{15}} = \frac{1}{3}$.

Câu 3: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Góc giữa hai đường thẳng $AA’$ và $BD$ bằng bao nhiêu độ?

A. ${30^ \circ }$.

B. ${60^ \circ }$.

C. ${45^ \circ }$.

D. ${90^ \circ }$.

Lời giải

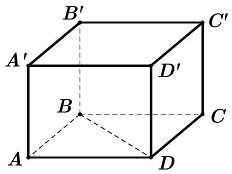
Ta có $AA’ \bot \left( {ABCD} \right) \Rightarrow AA’ \bot BD$.

Vậy $\left( {AA’,BD} \right) = {90^ \circ }$

Câu 4: Trong không gian cho hai đường thẳng phân biệt $a;b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Mệnh đề nào sau đây sai?

A. Nếu $b\parallel a$ thì $b \bot \left( P \right)$.

B. Nếu $b \bot a$ thì $b\parallel \left( P \right)$.

C. Nếu $b\parallel \left( P \right)$ thì $b \bot a$.

D. Nếu $b \bot \left( P \right)$ thì $b\parallel a$.

Lời giải

Mệnh đề sai là: Nếu $b \bot a$ thì $b\parallel \left( P \right)$.

Câu 5: Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc mặt đáy $\left( {ABC} \right)$. Góc tạo bởi $SB$ và đáy tương ứng là:

A. $\widehat {SCA}$

B. $\widehat {SBA}$.

C. $\widehat {SBC}$.

D. $\widehat {SAB}$.

Lời giải

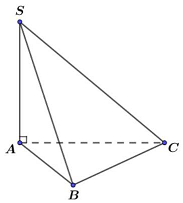
Ta có $SA \bot \left( {ABC} \right)$ nên hình chiếu của $SB$ xuống mặt đáy là $AB$ nên góc đó là $\widehat {SBA}$.

Câu 6: Với $a$ là số thực dương tùy ý, $\sqrt[3]{{{a^2}}}$ bằng:

A. ${a^{\frac{1}{6}}}$.

B. ${a^6}$.

C. ${a^{\frac{2}{3}}}$.

D. ${a^{\frac{3}{2}}}$.

Lời giải

Với mọi số thực dương $a$ ta có: $\sqrt[3]{{{a^2}}} = {a^{\frac{2}{3}}}$.

Câu 7: Với $x$ là số thực dương bất kỳ, biểu thức $P = \sqrt[3]{{\sqrt x }}$ bằng

A. ${x^{\frac{2}{3}}}$.

B. ${x^{\frac{5}{6}}}$.

C. ${x^{\frac{1}{6}}}$.

D. ${x^{\frac{3}{2}}}$.

Lời giải

Ta có biểu thức $P = \sqrt[3]{{\sqrt x }} = {\left( {\left( {{x^{\frac{1}{2}}}} \right)} \right)^{\frac{1}{3}}} = {x^{\frac{1}{2} \cdot \frac{1}{3}}} = {x^{\frac{1}{6}}}$

Câu 8: Cho $a,b > 0$ thỏa mãn ${a^{\frac{2}{3}}} > {a^{\frac{1}{2}}},{b^{\frac{2}{3}}} > {b^{\frac{3}{4}}}$. Khi đó khẳng định nào sau đây đúng?

A. $0 < a\left\langle {1,b} \right\rangle 1$.

B. $a > 1,0 < b < 1$.

C. $a > 1,b > 1$.

D. $0 < a < 1,0 < b < 1$.

Lời giải

Ta có $\frac{2}{3} > \frac{1}{2}$, do đó ${a^{\frac{2}{3}}} > {a^{\frac{1}{2}}}$ khi $a > 1$.

Lại có $\frac{2}{3} < \frac{3}{4}$, do đó ${b^{\frac{2}{3}}} > {b^{\frac{3}{4}}}$ khi $0 < b < 1$.

Vậy $a > 1,0 < b < 1$.

Câu 9: Cho $a,b$ là các số thực dương, $a \ne 1$ thỏa mãn ${log_a}b = 3$. Tính ${log_{\sqrt a }}{a^2}{b^3}$ ?

A. 24 .

B. 25 .

C. 22 .

D. 23 .

Lời giải

Ta có ${log_{\sqrt a }}{a^2}{b^3} = 2{log_a}\left( {{a^2}{b^3}} \right) = 2\left( {2 + 3{log_a}b} \right) = 2\left( {2 + 9} \right) = 22$.

Câu 10: Tập xác định của hàm số $y = {(x – 1)^{\sqrt 3 }}$ là

A. $\mathbb{R} \setminus \left\{ 1 \right\}$.

B. $\mathbb{R}$.

C. $\left( {1; + \infty } \right)$.

D. $\left( { – 1; + \infty } \right)$.

Lời giải

Điều kiện: $x – 1 > 0 \Leftrightarrow x > 1$. Vậy tập xác định của hàm số $y = {(x – 1)^{\sqrt 3 }}$ là $\left( {1; + \infty } \right)$.

Câu 11: Đường cong trong hình bên là của đồ thị hàm số nào sau đây?

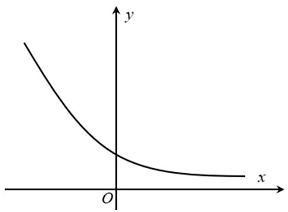
A. $y = {log_2}x$.

B. $y = {(0,8)^x}$.

C. $y = {log_{0,4}}x$.

D. $y = {(\sqrt 2 )^x}$.

Lời giải

Dựa vào đồ thị, ta có hàm số có tập xác định $\mathbb{R}$ và hàm số nghịch biến suy ra $y = {(0,8)^x}$.

Câu 12: Trong các khẳng định sau, khẳng định nào sai?

A. ${log_{{a^2} + 4}}\left( {{a^2} + 1} \right) \geqslant 0\forall a$.

B. ${4^{ – \sqrt 3 }} < {4^{ – \sqrt 2 }}$.

C. ${2^{30}} < {3^{20}}$.

D. $0,{99^\pi } > 0,{99^e}$.

Lời giải

Với $0 < a < 1$ thì ${a^m} > {a^n} \Leftrightarrow m < n$

Khi đó: $\left\{ {\begin{array}{*{20}{l}}
{0,99 < 1} \\
{\pi > e}
\end{array} \Rightarrow 0,{{99}^\pi } < 0,{{99}^e}} \right.$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Giả sử $A,B$ là hai điểm phân biệt trên đồ thị của hàm số $y = {log_3}\left( {5x – 3} \right)$ sao cho $A$ là trung điểm của đoạn $OB$.

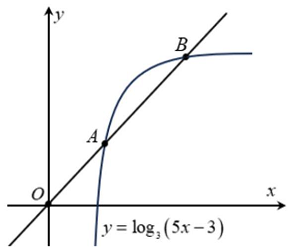
b) Trung điểm của đoạn thẳng $OB$ có tọa độ $\left( {\frac{{12}}{5};1} \right)$.

c) Gọi $H$ là hình chiếu của điểm $B$ xuống trục hoành. Khi đó ${S_{\vartriangle OBH}} = \frac{{\sqrt {61} }}{{25}}$

d) Đoạn thẳng $AB$ có độ dài bằng $\frac{{\sqrt {61} }}{5}$

Lời giải

Gọi $A\left( {{x_1},{log_3}\left( {5{x_1} – 3} \right)} \right)$. Vì $A$ là trung điểm $OB$ nên $B\left( {2{x_1};2{log_3}\left( {5{x_1} – 3} \right)} \right)$.

Vì $B$ thuộc đồ thị của hàm số $y = {log_3}\left( {5x – 3} \right)$ nên

$2{log_3}\left( {5{x_1} – 3} \right) = {log_3}\left( {10{x_1} – 3} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{5{x_1} – 3 > 0} \\
{10{x_1} – 3 > 0} \\
{{{\left( {5{x_1} – 3} \right)}^2} = 10{x_1} – 3}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{5{x_1} – 3 > 0} \\
{\left[ {\begin{array}{*{20}{c}}
{x = \frac{6}{5}} \\
{x = \frac{2}{5}}
\end{array}} \right.}
\end{array} \Leftrightarrow {x_1} = \frac{6}{5}} \right.} \right.$.

Vì thế $A\left( {\frac{6}{5};1} \right),B\left( {\frac{{12}}{5};2} \right) \Rightarrow AB = \frac{{\sqrt {61} }}{5}$.

Hình chiếu điểm $B$ xuống trục hoành là $H\left( {\frac{{12}}{5};0} \right) \Rightarrow BH = 2$ và $OH = \frac{{12}}{5} \Rightarrow {S_{\vartriangle OBH}} = \frac{{12}}{5}$

a) Đúng: Hoành độ của điểm $B$ là một số nguyên.

b) Sai: Trung điểm của đoạn thẳng $OB$ là điểm $A$ có tọa độ $\left( {\frac{6}{5};1} \right)$.

c) Sai: Gọi $H$ là hình chiếu của điểm $B$ xuống trục hoành. Khi đó ${S_{\vartriangle OBH}} = \frac{{12}}{5}$

d) Đúng: Đoạn thẳng $AB$ có độ dài bằng $\frac{{\sqrt {61} }}{5}$.

Câu 2: Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B,AB = BC = a$. Cạnh bên $SA$ vuông góc với mặt phẳng đáy $\left( {ABC} \right)$ và $SA = a$. Gọi $I$ là trung điểm của $AC$ và kẻ $IH \bot SC$.

a) Đường thẳng $SC$ vuông góc với mặt phẳng $\left( {BHI} \right)$

b) Cosin góc tạo bởi hai đường thẳng $IH$ và $BH$ bằng $\frac{{\sqrt 3 }}{2}$.

c) Độ dài đoạn thẳng $BH$ bằng $\frac{{a\sqrt 2 }}{2}$

d) Góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBC} \right)$ bằng ${60^ \circ }$.

Lời giải

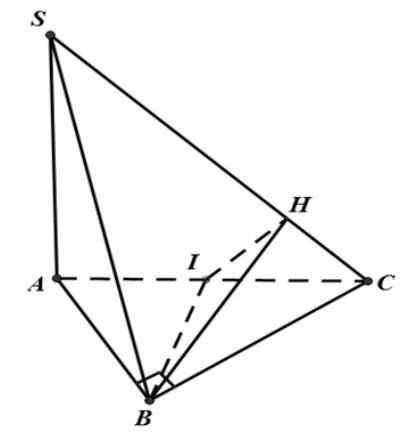
Ta có $\left( {SAC} \right) \cap \left( {SBC} \right) = SC$. Do $SA \bot \left( {ABC} \right) \Rightarrow \left( {SAC} \right) \bot \left( {ABC} \right)$.

Kẻ $BI \bot AC \Rightarrow BI \bot \left( {SAC} \right) \Rightarrow BI \bot SC$

Kẻ $IH \bot SC$ (2).

Từ (1) và (2) ta có $\left( {BIH} \right) \bot SC$. Mặt khác: $\left( {SAC} \right) \cap \left( {BIH} \right) = IH;\left( {SBC} \right) \cap \left( {BIH} \right) = BH$

Do đó $\overline {\left( {\left( {SAC} \right);\left( {SBC} \right)} \right)} = \overline {\left( {IH;BH} \right)} $.

Xét tam giác $SBC$ có $\widehat {CBS} = {90^ \circ }$ (vì $BC \bot BA \Rightarrow BC \bot SB$

$BC = a;SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 2 ;BH \bot SC \Rightarrow \frac{1}{{B{H^2}}} = \frac{1}{{B{S^2}}} + \frac{1}{{B{C^2}}} \Rightarrow BH = \frac{{a\sqrt 6 }}{3}.$

Xét tam giác $BHI$ có $BI \bot HI;BI = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2};BH = \frac{{a\sqrt 6 }}{3}$

$ \Rightarrow sin\widehat {BHI} = \frac{{BI}}{{BH}} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {BHI} = {60^ \circ }$

Vậy $\overline {\left( {\left( {SAC} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {IH;BH} \right)} = \widehat {BHI} = {60^ \circ }$.

a) Đúng: Đường thẳng $SC$ vuông góc với mặt phẳng $\left( {BHI} \right)$

b) Sai: Cosin góc tạo bởi hai đường thẳng $IH$ và $BH$ bằng $\frac{1}{2}$.

c) Sai: Độ dài đoạn thẳng $BH$ bằng $\frac{{a\sqrt 6 }}{3}$

d) Đúng: Góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBC} \right)$ bằng ${60^ \circ }$.

Câu 3: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

a) Tổng số học sinh được khảo sát là 42 học sinh.

b) Giá trị đại diện của nhóm $\left[ {20;40} \right)$ là 25 .

c) Số trung bình của mẫu số liệu trên thuộc nhóm $\left[ {0;20} \right)$.

d) Có 16 học sinh tập thể dục ít nhất 1 giờ trong ngày.

Lời giải

Tổng số học sinh được khảo sát là: $5 + 9 + 12 + 10 + 6 = 42$.

Giá trị đại diện của nhóm $\left[ {20;40} \right)$ là $\frac{{20 + 40}}{2} = 30$.

Số trung bình của mẫu số liệu trên là: .

Số học sinh tập thể dục ít nhất 1 giờ trong ngày: $10 + 6 = 16$ học sinh

a) Đúng: Tổng số học sinh được khảo sát là: $5 + 9 + 12 + 10 + 6 = 42$.

b) Sai: Giá trị đại diện của nhóm $\left[ {20;40} \right)$ là 30 .

c) Sai: Số trung bình của mẫu số liệu trên thuộc nhóm [40;60).

d) Đúng: Có 16 học sinh tập thể dục ít nhất 1 giờ trong ngày.

Câu 4: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Biết $SA = a\sqrt 2 $ và $SA$ vuông góc với mặt đáy. Gọi $M$ là trung điểm của $BC$ và $H$ là hình chiếu vuông góc của $A$ lên $SM$.

a) Đường thẳng $AH$ vuông góc với mặt phẳng $\left( {SBC} \right)$

b) Đường thẳng $SH$ là hình chiếu của đường thẳng $SA$ lên mặt phẳng $\left( {SBC} \right)$

c) Độ dài đoạn thẳng $AH$ bằng $\frac{{6a}}{{11}}$

d) Cosin góc tạo bởi đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ bằng $\frac{{\sqrt {11} }}{{33}}$.

Lời giải

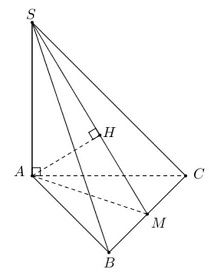
Gọi $M$ là trung điểm của $BC$ và $H$ là hình chiếu vuông góc của $A$ lên $SM$.

Ta có: $AH \bot SM$.

Mặt khác $BC \bot \left( {SAM} \right)$ nên $BC \bot AH$. Ta suy ra $AH \bot \left( {SBC} \right)$.

Nên $SH$ là hình chiếu của $SA$ lên mặt phẳng $\left( {SBC} \right)$.

Ta suy ra góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ là góc $\alpha = \widehat {ASH}$.

Xét tam giác $SAM$ vuông tại $A$ ta có: $\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}} = \frac{1}{{{{(a\sqrt 2 )}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{11}}{{6{a^2}}}$

$ \Rightarrow A{H^2} = \frac{{6{a^2}}}{{11}} \Rightarrow AH = \frac{{a\sqrt {66} }}{{11}}$.

Xét tam giác $SAH$ vuông tại $H$ ta có: $sin\widehat {ASH} = \frac{{AH}}{{SA}} = \frac{{\frac{{a\sqrt {66} }}{{11}}}}{{a\sqrt 2 }} = \frac{{\sqrt {33} }}{{11}}$.

a) Đúng: Đường thẳng $AH$ vuông góc với mặt phẳng $\left( {SBC} \right)$.

b) Đúng: Đường thẳng $SH$ là hình chiếu của đường thẳng $SA$ lên mặt phẳng $\left( {SBC} \right)$

c) Sai: Độ dài đoạn thẳng $AH$ bằng $\frac{{6a}}{{11}}$

d) Sai: Cosin góc tạo bởi đường thẳng $SA$ và mặt phẳng $\left( {SBC} \right)$ bằng $\frac{{\sqrt {33} }}{{11}}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Tứ phân vị thứ nhất ${Q_1}$ của mẫu số liệu ghép nhóm này (Kết quả làm tròn đến hàng trăm)

Lời giải

Cỡ mẫu: $n = 5 + 9 + 12 + 10 + 6 = 42$.

Nhóm chứa tứ phân vị thứ nhất: $\left[ {20;40} \right)$. Suy ra: ${u_m} = 20$ và ${u_{m + 1}} = 40$.

Ta có ${n_m} = 9,C = 5$.

Vậy tứ phân vị thứ nhất ${Q_1}$ của mẫu số liệu ghép nhóm là:

${Q_1} = 20 + \frac{{\frac{{42}}{4} – 5}}{9} \cdot \left( {40 – 20} \right) = \frac{{290}}{9} \approx 32,22$.

Câu 2: Cho tập $A = \left\{ {0;1;2;3;4;5} \right\}$. Gọi $S$ là tập các số tự nhiên có 5 chữ số khác nhau lập từ $A$. Lấy từ $S$ một phần tử, tính xác suất để số lấy được là một số chia hết cho 5.

Lời giải

Số phần tử của không gian mẫu là: $n\left( \Omega \right) = 5 \cdot A_5^4 = 600$.

Gọi $E$ là biến cố: “Số lấy được là một số chia hết cho 5 “.

Gọi số cần tìm là $x = \overline {{a_1}{a_2}{a_3}{a_4}{a_5}} $, (với ${a_1} \ne 0;{a_1},{a_2},{a_3}{a_4},{a_5} \in A$ ).

$x \vdots 5 \Rightarrow {a_5} \in \left\{ {0;5} \right\}$.

Với ${a_5} = 0:$ ta có $A_5^4$ số.

Với ${a_5} = 5:$ ta có $4.A_4^3$ số.

Do đó $n\left( E \right) = A_5^4 + 4.A_4^3 = 216$.

Vậy xác suất cần tìm là $P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = \frac{{216}}{{600}} = \frac{9}{{25}} = 0,36$.

Câu 3: Mức sản xuất của một hãng DVD trong một ngày là $q\left( {m,n} \right) = {m^{\frac{2}{3}}}{n^{\frac{1}{3}}}$. Trong đó $m$ là số lượng nhân viên và $n$ là số lao động chính. Mỗi ngày hãng phải sản xuất 40 sản phẩm để đáp ứng nhu cầu của khách hàng. Biết rằng lương của nhân viên là $16\$ $ / ngày và lương của lao động chính là $27\$ $/ngày. Giá trị nhỏ nhất chi phí một ngày của hãng sản xuất này là bao nhiêu $\$ $ ?

Lời giải

Theo giả thiết ta có: ${m^{\frac{2}{3}}}{n^{\frac{1}{3}}} \geqslant 40 \Leftrightarrow {m^2}n \geqslant 64000$ với $m;n \in {\mathbb{N}^*}$.

Tổng số tiền phải chi trong một ngày là: $T = 16m + 27n = 8m + 8m + 27n \geqslant 3\sqrt[3]{{1728{m^2}n}} \geqslant 1440$.

Suy ra $MinT = 1440$.

Dấu “=” xảy ra khi $\left\{ {\begin{array}{*{20}{c}}
{8m = 27n} \\
{{m^2}n \geqslant 64000}
\end{array}} \right.$.

Vậy chi phí thấp nhất để trả cho 57 nhân viên và 17 lao động chính để sản xuất đạt yêu cầu là 1440 $.

Câu 4: Một chiếc máy có hai động cơ $I$ và $II$ chạy độc lập nhau. Xác suất để động cơ $I$ và $II$ chạy tốt lần lượt là 0,8 và 0,7 . Tính xác suất để ít nhất một động cơ chạy tốt

Lời giải

Gọi $A$ là biến cố: “Có ít nhất một động cơ chạy tốt”.

Gọi $B$ là biến cố: “Chỉ động cơ $I$ chạy tốt”.

$P\left( B \right) = 0,8.\left( {1 – 0,7} \right) = 0,24$.

Gọi $C$ là biến cố: “Chỉ động cơ II chạy tốt”.

$P\left( C \right) = \left( {1 – 0,8} \right) \cdot 0,7 = 0,14$.

Gọi $D$ là biến cố: “Cả hai động cơ đều chạy tốt”.

$P\left( D \right) = 0,8 \cdot 0,7 = 0,56$.

Vậy $P\left( A \right) = 0,24 + 0,14 + 0,56 = 0,94$.

Câu 5: Năm 2020 , một hãng xe ô tô niêm yết giá bán loại xe $X$ là 850.000 .000 đồng và dự định trong 10 năm tiếp theo, mỗi năm giảm $2\% $ giá bán so với giá bán của năm liền trước. Theo dự định đó, năm 2025 hãng xe ô tô niêm yết giá bán loại xe $X$ là bao nhiêu (đơn vị: triệu đồng) (Kết quả làm tròn đến hàng đơn vị)?

Lời giải

Theo đề bài, ta có

Giá niêm yết xe $X$ năm 2021 là: ${G_{2021}} = 850x\left( {1 – 2\% } \right)$

Giá niêm yết xe $X$ năm 2022 là: ${G_{2022}} = {G_{2021}}\left( {1 – 2\% } \right) = 850x{(1 – 2\% )^2}$

Vậy giá niêm yết xe $X$ năm 2025 là: ${G_{2025}} = 850x{(1 – 2\% )^5} \approx 768$ dồng.

Câu 6: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$, cạnh bên $SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 ,AD = 2AB = 2BC = 2a$. Tính côsin của góc giữa 2 mặt phẳng $\left( {SAD} \right)$ và $\left( {SCD} \right)$.

Lời giải

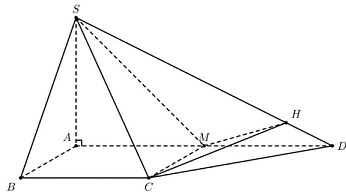
Gọi $M$ là trung điểm $AD$ thì $ABCM$ là hình vuông nên $CM \bot AD$ suy ra $CM \bot \left( {SAD} \right)$.

Kẻ $MH \bot SD\left( {H \in SD} \right)$ thì $SD \bot \left( {CMH} \right)$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{\left( {SAD} \right) \cap \left( {SCD} \right) = SD} \\
{SD \bot \left( {CMH} \right)}
\end{array}} \right.$ nên góc giữa $\left( {SAD} \right)$ và $\left( {SCD} \right)$ là góc $\widehat {MHC}$.

Trong $\vartriangle SAD$ thì $tan\widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{\sqrt 2 }}{2} \Rightarrow sin\widehat {SDA} = \frac{{\sqrt 3 }}{3}$

Trong $\vartriangle MHD$ vuông tại $H$ thì $sin\widehat {SDA} = \frac{{MH}}{{MD}} \Rightarrow MH = \frac{{a\sqrt 3 }}{3}$.

Trong $\vartriangle MHC$ vuông tại $M$ thì $HC = \sqrt {M{C^2} + M{H^2}} = \sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{2a\sqrt 3 }}{3}$

Khi đó: $cos\widehat {MHC} = \frac{{MH}}{{HC}} = \frac{{\frac{{a\sqrt 3 }}{3}}}{{\frac{{2a\sqrt 3 }}{3}}} = \frac{1}{2} = 0,5$.