Các Dạng Toán Bài Hai Đường Thẳng Vuông Góc Lớp 11 Giải Chi Tiết

Các dạng toán bài hai đường thẳng vuông góc lớp 11 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
I. DẠNG 1. XÁC ĐỊNH GÓC GIỮA HAI ĐƯỜNG THẲNG

Phương pháp:

Góc giữa hai đường thẳng $m$ và $n$ trong không gian, kí hiệu $\left( {m,n} \right)$, là góc giữa hai đường thẳng $a$ và $b$ cùng đi qua một điểm và tương ứng song song với $m$ và $n$.

Chú ý

• Để xác định góc giữa hai đường thẳng chéo nhau $a$ và $b$, ta có thể lấy một điểm $O$ thuộc đường thẳng $a$ và qua đó kẻ đường thẳng $b’$ song song với $b$. Khi đó $\left( {a,b} \right) = \left( {a,b’} \right)$.

• Với hai đường thẳng $a,b$ bất kì: ${0^ \circ } \leqslant \left( {a,b} \right) \leqslant {90^ \circ }$.

Câu 1: Cho hình chóp $S.ABCD$ có đáy ABCD là hình bình hành. Tam giác $SAD$ vuông tại $A$ và $\widehat {ASD} = {50^0}$. Tính các góc $\left( {BC,SA} \right),\,\,\left( {SD,BC} \right)$.

Lời giải

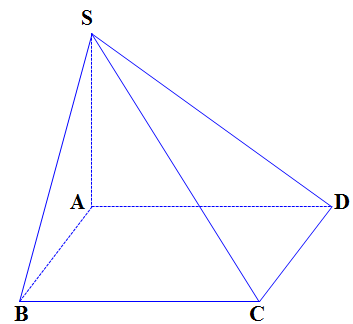
a) Tính góc $\left( {BC,SA} \right)$.

Ta có: $BC//AD$ nên $\left( {AD,SA} \right) = {90^0}$

b) Tính góc $\left( {SD,BC} \right)$.

Ta có: $BC//AD$ nên $\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA} = {180^0} – {50^0} = {130^0}$

Câu 2: Cho hình hộp $ABCD \cdot A’B’C’D’$ có các mặt là các hình vuông. Tính các góc $\left( {AA’,CD} \right),\left( {A’C’,BD} \right),\left( {AC,DC’} \right)$.

Lời giải

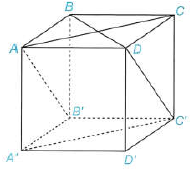
a) Tính góc $\left( {AA’,CD} \right)$.

Ta có: $CD//AB$ nên $\left( {AA’,CD} \right) = \left( {AA’,AB} \right) = {90^ \circ }$.

b) Tính góc $\left( {A’C’,BD} \right)$.

Tứ giác $ACC’A’$ có các cặp cạnh đối bằng nhau nên nó là một hình bình hành.

Do đó, $A’C’//AC$.

Vậy $\left( {A’C’,BD} \right) = \left( {AC,BD} \right) = {90^ \circ }$.

c) Tính góc $\left( {AC,DC’} \right)$.

Tương tự, $DC’//AB’$.

Vậy $\left( {AC,DC’} \right) = \left( {AC,AB’} \right)$. Tam giác $AB’C$ có ba cạnh bằng nhau (vì là các đường chéo của các hình vuông có độ dài cạnh bằng nhau) nên $AB’C$ là một tam giác đều.

Suy ra, $\left( {AC,DC’} \right) = \left( {AC,AB’} \right) = {60^ \circ }$.

Câu 3: Cho hình lăng trụ $ABC \cdot A’B’C’$ có các đáy là các tam giác đều. Tính góc $\left( {AB,B’C’} \right)$

Lời giải

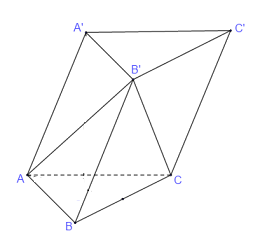
Ta có: $\left( {AB,B’C’} \right) = \left( {AB,BC} \right) = {60^ \circ }$.

Câu 4: Cho hình lăng trụ $ABC \cdot A’B’C’$ có tam giác $ABC$ cân tại $A$ và $\widehat {BAC} = {120^ \circ }$. Các điểm $M,N$ lần lượt thuộc hai đoạn thẳng $AA’$ và $BB$ ‘ thoả mãn $MN//AB$, các điểm $P,Q$ lần lượt thuộc hai đoạn thẳng $AA’$ và $CC'(P$ khác $M$ ) thoả mãn $PQ//AC$. Tính các góc sau:

a) $\left( {AB,AC} \right)$;

b) $\left( {AB,B’C’} \right)$;

c) $\left( {MN,PQ} \right)$.

Lời giải

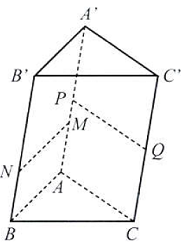
a) Trong mặt phẳng $\left( {ABC} \right)$, vì $\widehat {BAC} = {120^ \circ }$ nên $\left( {AB,AC} \right) = {180^ \circ } – {120^ \circ } = {60^ \circ }$.

b) Vì tam giác $ABC$ cân tại $A$ nên $\widehat {ABC} = \widehat {ACB} = \frac{{{{180}^ \circ } – \widehat {BAC}}}{2} = \frac{{{{180}^ \circ } – {{120}^ \circ }}}{2} = {30^ \circ }$.

Ta có $BC//B’C’$ nên $\left( {AB,B’C’} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {30^ \circ }$.

c) Vì $MN//AB,PQ//AC$ nên $\left( {MN,PQ} \right) = \left( {AB,AC} \right) = {60^ \circ }$.

Câu 5: Cho tứ diện $ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $AB$ và $CD$. Tính góc giữa hai đường thẳng $AD$ và $BC$, biết $MN = a\sqrt 3 $ và $AD = BC = 2a$.

Lời giải

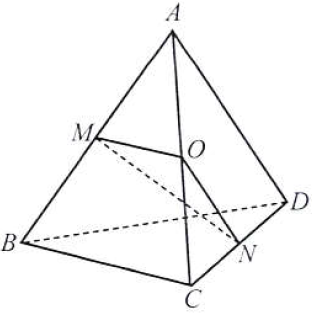
Gọi $O$ là trung điểm $AC$.

Vì $OM,ON$ lần lượt là đường trung bình của hai tam giác $ABC,CAD$ nên $OM//BC,ON//AD$ và

$OM = \frac{1}{2}CB = a,ON = \frac{1}{2}AD = a$. Khi đó $\left( {AD,BC} \right) = \left( {ON,OM} \right)$.

Xét tam giác $OMN$ có:

${\text{cos}}\widehat {MON} = \frac{{O{M^2} + O{N^2} – M{N^2}}}{{2OM \cdot ON}} = \frac{{{a^2} + {a^2} – {{(a\sqrt 3 )}^2}}}{{2a \cdot a}} = – \frac{1}{2}$ nên $\widehat {MON} = {120^ \circ }$.

Suy ra $\left( {AD,BC} \right) = \left( {ON,OM} \right) = {180^ \circ } – {120^ \circ } = {60^ \circ }$.

Vậy góc giữa hai đường thẳng $AD$ và $BC$ bằng ${60^ \circ }$.

Câu 6: Cho tứ diện $ABCD$ có tất cả các cạnh bằng nhau. Gọi $M,N,K$ lần lượt là trung điểm của các cạnh $AC,BC$ và $AB$. Tính góc giữa đường thẳng $MN$ và $BD$; góc giữa đường thẳng $KN$ và $MD$.

Lời giải.

Vì $MN//AB$ nên góc giữa hai đường thẳng $MN$ và $BD$ bằng góc giữa hai đường thẳng $AB$ và $BD$, mà tam giác $ABD$ là tam giác đều nên góc giữa hai đường thẳng $AB$ và $BD$ bằng ${60^ \circ }$.

Do đó $\left( {MN,BD} \right) = \left( {AB,BD} \right) = {60^ \circ }$.

Vì $NK//AC$ nên góc giữa hai đường thẳng $NK$ và $MD$ bằng góc giữa hai đường thẳng $AC$ và $MD$, mà tam giác $ACD$ là tam giác đều nên góc giữa hai đường thẳng $AC$ và $MD$ bằng ${90^ \circ }$. Do đó $\left( {NK,MD} \right) = \left( {AC,MD} \right) = {90^ \circ }$.

Câu 7: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành, tam giác $SAD$ là tam giác đều và $M$ là trung điểm của cạnh $AD$. Tính góc giữa hai đường thẳng $BC$ và $SA;BC$ và $SM$.

Lời giải

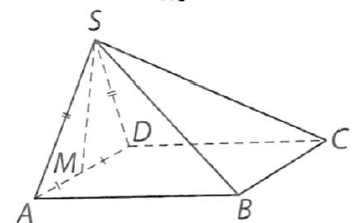
Vì $BC//AD$ nên $\left( {BC,SA} \right) = \left( {AD,SA} \right) = \widehat {SAD} = {60^ \circ }$ và $\left( {BC,SM} \right) = \left( {AD,SM} \right) = {90^ \circ }$.

Câu 8: Cho hình hộp $ABCD \cdot A’B’C’D’$ có tất cả các cạnh bằng nhau và góc $A’AD$ bằng ${120^ \circ }$. Tính góc giữa các cặp đường thẳng sau: $A’C’$ và $BD;AD$ và $BB’;A’D$ và $BB’$.

Lời giải

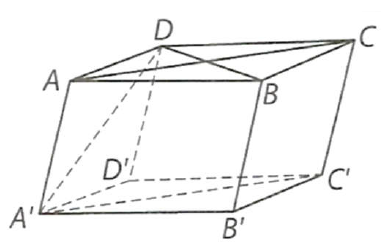
Vì $ABCD$ là hình thoi và $A’C’//AC$ nên $\left( {A’C’,BD} \right) = \left( {AC,BD} \right) = {90^ \circ }$.

Vì $BB’//AA’$ nên $\left( {AD,BB’} \right) = \left( {AD,AA’} \right) = {180^ \circ } – \widehat {A’AD} = {60^ \circ }$ và $\left( {A’D,BB’} \right) = \left( {A’D,AA’} \right) = \widehat {AA’D} = {30^ \circ }$.

Câu 9: Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông tâm $O$ và tất cả các cạnh của hình chóp đều bằng $a$. Gọi $M,N$ lần lượt là trung điểm các cạnh $SA,AB$.

a) Tính góc giữa các cặp đường thẳng sau: $MN$ và $SD;MO$ và $SB$.

b) Tính tang của góc giữa hai đường thẳng $SN$ và $BC$.

Lời giải

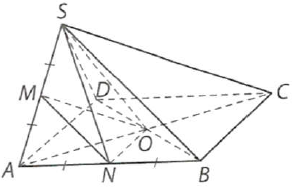
a) Ta có: $B{D^2} = S{B^2} + S{D^2} = 2{a^2}$ nên $\vartriangle SBD$ vuông tại $S$, mà $MN//SB$, suy ra $\left( {MN,SD} \right) = \left( {SB,SD} \right) = {90^ \circ }$.

Với $O$ là giao điểm của $AC$ và $BD$ thì $MO//SC$.

Khi đó $\left( {MO,SB} \right) = \left( {SC,SB} \right) = \widehat {BSC} = {60^ \circ }$.

b) Vì $ON//BC$ nên $\left( {SN,BC} \right) = \left( {SN,ON} \right) = \widehat {SNO}$.

Ta có $SO = \frac{{a\sqrt 2 }}{2};ON = \frac{a}{2}$ và tam giác $SNO$vuông tại $O$ nên ${\text{tan}}\widehat {SNO} = \frac{{SO}}{{ON}} = \sqrt 2 $. Vậy ${\text{tan}}\left( {SN,BC} \right) = \sqrt 2 $.

Câu 10: Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình thoi cạnh $a,SA = a\sqrt 3 ,SA \bot BC$.

Gọi $I,J$ lần lượt là trung điểm của $SA,SC$. Tính góc giữa các cặp đường thẳng:

a) $IJ$ và $BD$;

b) $SD$ và $BC$.

Lời giải

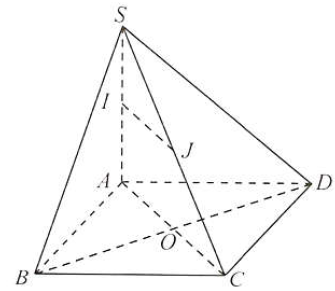
a) $\vartriangle SAC$ có $I,J$ lần lượt là trung điểm của $SA,SC$, suy ra $IJ$ là đường trung bình của $\vartriangle SAC$, suy ra $IJ//AC$.

Gọi $O$ là giao điểm của $AC$ và $BD$.

Vậy $\left( {IJ,BD} \right) = \left( {AC,BD} \right) = \widehat {AOB} = {90^ \circ }$.

b) Ta có $AD//BC$, suy ra $\left( {SD,BC} \right) = \left( {SD,AD} \right)$.

Mặt khác: $\left\{ {\begin{array}{*{20}{l}}
{SA \bot BC} \\
{BC//AD}
\end{array} \Rightarrow SA \bot AD} \right.$.

Vậy $\vartriangle SAD$ vuông tại $A$.

Suy ra ${\text{tan}}\widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 $.

Suy ra $\widehat {SDA} = {60^ \circ }$.

Vậy $\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA} = {60^ \circ }$.

Câu 11: Cho tứ diện $ABCD$ có $AB = CD = 2a$. Gọi $M,N$ lần lượt là trung diểm của $BC,AD$. Cho biết $MN = a\sqrt 3 $, tính góc giữa $AB$ và $CD$.

Lời giải

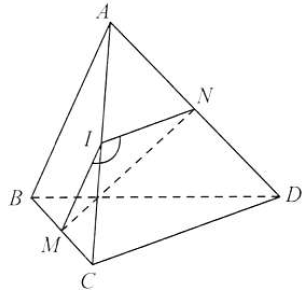
Gọi $I$ là trung điểm $AC$.

$\vartriangle ABC$ có $I,M$ lần lượt là trung điểm của $AC,BC$, suy ra $IM$ là đường trung bình của $\vartriangle ABC$, suy

ra $IM//AB$ và $IM = \frac{1}{2}AB = a$.

Tương tự, ta có $IN//CD$ và $IN = a$.

Ta có $IM//AB$ và $IN//CD$, suy ra $\left( {AB,CD} \right) = \left( {IM,IN} \right)$. Áp dụng định lí côsin trong tam giác $MIN$

$M{N^2} = I{M^2} + I{N^2} – 2 \cdot IM \cdot IN \cdot {\text{cos}}\widehat {MIN}$

$ \Rightarrow 3{a^2} = {a^2} + {a^2} – 2 \cdot a \cdot a \cdot {\text{cos}}\widehat {MIN}$

$ \Rightarrow {\text{cos}}\widehat {MIN} = \frac{{3{a^2} – 2{a^2}}}{{ – 2{a^2}}} = – \frac{1}{2}$

$ \Rightarrow \widehat {MIN} = {120^ \circ }$.

Vậy $\left( {AB,CD} \right) = \left( {IM,IN} \right) = {180^ \circ } – \widehat {MIN} = {180^ \circ } – {120^ \circ } = {60^ \circ }$.

Câu 12: Cho tứ diện đều $ABCD,M$ là trung điểm của cạnh $BC$. Tính góc giữa $AB$ và $DM$.

Lời giải

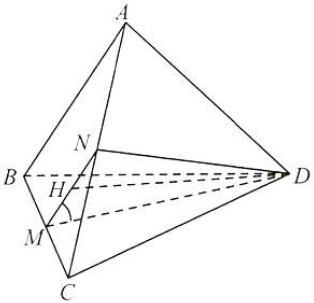
Đặt $2a$ là độ dài cạnh của tứ diện đều.

Gọi $N$ là trung điểm của $AC,H$ là trung điểm của $MN$, ta có:

$MN//AB$, suy ra $\left( {AB,DM} \right) = \left( {MN,DM} \right)$.

$DM = DN = a\sqrt 3 ,MN = a$ nên $\vartriangle DMN$ cân tại $D$.

Suy ra $MH = \frac{a}{2}$ và $DH \bot MN$.

${\text{cos}}\widehat {DMN} = \frac{{MH}}{{MD}} = \frac{{\sqrt 3 }}{6} \Rightarrow \widehat {DMN} \approx 73,{2^ \circ }$.

Vậy $\left( {AB,DM} \right) = \left( {MN,DM} \right) = \widehat {DMN} \approx 73,{2^ \circ }$.

Câu 13: Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $a,SA = a\sqrt 3 ,SA \bot AC$,

$SA \bot BC,\widehat {BAD} = {120^ \circ }$. Gọi $M,N$ lần lượt là trung điểm của $AD,BC$. Tính góc giữa các cặp đường thẳng:

a) $SD$ và $BC$.

b) $MN$ và $SC$.

Lời giải

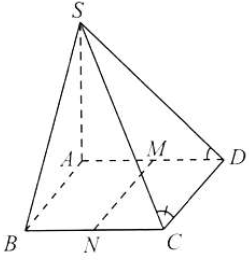
a) Vì $AD//BC$ nên $\left( {SD,BC} \right) = \left( {SD,AD} \right)$.

Vì $SA \bot BC$ và $AD//BC$ nên $SA \bot AD$ hay tam giác $SAD$ vuông tại $A$.

Do đó $\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA} = {60^ \circ }$.

b) Vì $MN//CD$ nên $\left( {SC,MN} \right) = \left( {SC,CD} \right)$.

Vì $ABCD$ là hình thoi cạnh $a$ có $\hat A = {120^ \circ }$ nên $ACD$ là tam giác đều cạnh $a$.

Xét các tam giác vuông $SAC,SAD$ có:

$SC = \sqrt {A{C^2} + S{A^2}} = \sqrt {{a^2} + 3{a^2}} = 2a$ và $SD = \sqrt {A{D^2} + S{A^2}} = \sqrt {{a^2} + 3{a^2}} = 2a$.

Áp dụng định lí côsin trong tam giác $SCD$ :

${\text{cos}}\widehat {SCD} = \frac{{S{C^2} + C{D^2} – S{D^2}}}{{2 \cdot SC \cdot CD}} = \frac{1}{4} \Rightarrow \widehat {SCD} \approx 75,{5^ \circ }$.

Vậy $\left( {SC,MN} \right) = \left( {SD,AD} \right) = \widehat {SCD} = 75,{5^ \circ }$.

Câu 14: Cho hình chóp tứ giác $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $M,N,I,J$ lần lượt là trung điểm của $SA,SD,SC$ và $BC$. Tính góc giữa các cặp đường thẳng sau:

a) $IJ$ và $DC$;

b) $MN$ và $IJ$.

Lời giải

a) Ta có $IJ//SB,DC//AB$, suy ra $\left( {IJ,DC} \right) = \left( {SB,AB} \right) = \widehat {SBA} = {60^ \circ }$.

b) Ta có $MN//AD//BC,IJ//SB$, suy ra $\left( {MN,IJ} \right) = \left( {BC,SB} \right) = \widehat {SBC} = {60^ \circ }$.

Câu 15: Cho hình chóp $S.ABC$ có $AB = AC,\widehat {SAC} = \widehat {SAB}$. Tính số đo của góc giữa hai đường thẳng $SA$ và $BC$.

Lời giải

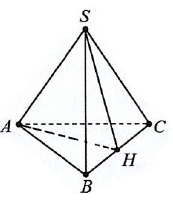
Cách 1:

Ta có: $\overrightarrow {AS} \cdot \overrightarrow {BC} = \overrightarrow {AS} \cdot \left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \overrightarrow {AS} \cdot \overrightarrow {AC} – \overrightarrow {AS} \cdot \overrightarrow {AB} $

$ = AS \cdot AC \cdot {\text{cos}}\widehat {SAC} – AS \cdot AB \cdot {\text{cos}}\widehat {SAB} = 0$

Do đó số đo của góc giữa hai đường thẳng $SA$ và $BC$ bằng 90 .

Cách 2:

Vì $AB = AC,\widehat {SAC} = \widehat {SAB}$ nên $\vartriangle SAC = \vartriangle SAB$, suy ra $SB = SC$, do đó hai tam giác $ABC$ và $SBC$ là tam giác cân. Chứng minh tương tự bài 1 (trang 194) ta được $SA \bot BC$.

Câu 16: Cho hình hộp $ABCD \cdot A’B’C’D’$ có 6 mặt là hình vuông. Tính số đo của góc giữa hai đường thẳng $A’C’$ và $BD$.

Lời giải

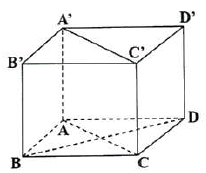
$AC//A’C’$ nên $\left( {A’C’;BD} \right) = \left( {AC;BD} \right) = 90$.

Câu 17: Cho hình hộp $ABCD \cdot A’B’C’D’$ có 6 mặt là hình vuông. Tính số đo của góc giữa hai đường thẳng $BA’$ và $CD$.

Lời giải

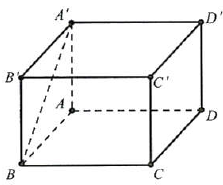
Có $CD//AB \Rightarrow \left( {BA’,CD} \right) = \left( {BA’,BA} \right) = \widehat {ABA’} = {45^ \circ }$ (do $ABB’A’$ là hình vuông).

Câu 18: Cho tứ diện đều $ABCD$. Gọi $M$ là trung điểm của cạnh $BC$. Côsin của góc giữa hai đường thẳng $AB$ và $DM$ bằng?

Lời giải

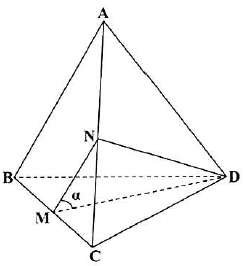
Kẻ $MN//AB$, có $MN$ là đường trung bình của $\vartriangle ABC$.

Suy ra $MN = \frac{{AB}}{2}$.

Do đó: $\left( {AB,DM} \right) = \left( {MN,DM} \right) = \widehat {DMN} = \alpha $.

Gọi tứ diện đều $ABCD$ có cạnh bằng $a$.

$MN = \frac{a}{2},DN = DM = \frac{{a\sqrt 3 }}{2}$

$ \Rightarrow {\text{cos}}\alpha = \frac{{M{N^2} + D{M^2} – D{N^2}}}{{2 \cdot MN \cdot DM}} = \frac{{\sqrt 3 }}{6}$.

Câu 19: Cho hình hộp $ABCD \cdot A’B’C’D’$ có 6 mặt là hình vuông cạnh bằng $a$. Gọi $M,N$ lần lượt là trung điểm của cạnh $AA’$ và $A’B’$. Tính số đo góc giữa hai đường thẳng $MN$ và $BD$.

Lời giải

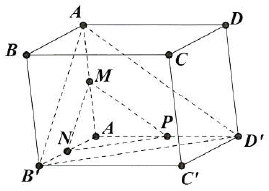
Gọi $P$ là trung điểm cạnh $AD’$.

Vì $ABCD \cdot A’B’C’D’$ là hình lập phương cạnh $a$ nên $AB’ = B’D’ = D’A = a\sqrt 2 $.

Suy ra $MN = NP = PM = \frac{{a\sqrt 2 }}{2}$

$ \Rightarrow \left( {MN,BD} \right) = \left( {MN,NP} \right) = {60^ \circ }$.

Câu 20: Cho hình lăng trụ tam giác $ABC \cdot A’B’C’$ có đáy $ABC$ là tam giác cân $AB = AC = a$, $\widehat {BAC} = {120^ \circ }$, cạnh bên $AA’ = a\sqrt 2 $ và $AA’ \bot AB,AA’ \bot AC$. Tính góc giữa hai đường thẳng $AB’$ và $BC$.

Lời giải

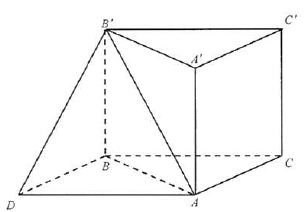
Trong $\left( {ABC} \right)$, kẻ $AD$ sao cho $ACBD$ là hình bình hành.

Ta có: $BC//AD$ nên $\left( {AB’;BC} \right) = \left( {AB’;AD} \right) = \widehat {B’AD}$.

Ta có: $AD = BC = a\sqrt 3 ,AB’ = \sqrt {A{B^2} + A{B^2}} = a\sqrt 3 $,

$DB’ = \sqrt {B{B^{{\text{‘}}2}} + A{C^2}} = a\sqrt 3 $.

Vậy tam giác $B’AD$ đều nên $\widehat {B’AD} = {60^ \circ }$.

Câu 21: Cho hình chóp $S.ABC$ có $SA,SB,SC$ đôi một vuông góc với nhau và $SA = SB = SC = a$. Gọi $M$ là trung điểm của $AB$. Tính góc giữa hai đường thẳng $SM$ và $BC$.

Lời giải

Gọi $N$ là trung điểm của $AC$. Khi đó góc giữa $SM$ và $BC$ bằng góc giữa $SM$ và $MN$.

Ta có: $AB = BC = CA$

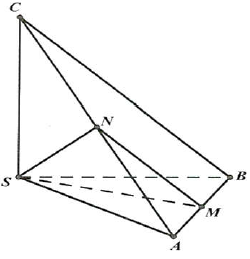
$SM = \frac{1}{2}AB$ (trung tuyến trong tam giác vuông ứng với cạnh huyền).

$SN = \frac{1}{2}AC$ (trung tuyến trong tam giác vuông ứng với cạnh huyền).

$MN = \frac{1}{2}BC$.

Suy ra $SM = MN = SN$ hay tam giác $SMN$ dều.

Do đó $\left( {SM;BC} \right) = \widehat {SMN} = {60^ \circ }$.

Câu 22: Cho hình hộp $ABCD \cdot A’B’C’D’$ có 6 mặt là hình vuông. Tính số đo của góc giữa hai đường thẳng $AC$ và $A’D$ ?

Lời giải

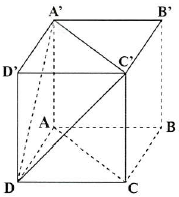
Ta có: $\left( {AC,A’D} \right) = \left( {A’C’,A’D} \right) = \widehat {DA’C’} = {60^ \circ }$.

Vì $A’D = A’C’ = C’D$.

Câu 23: Cho tứ diện $ABCD$ có $AB$ vuông góc với $\left( {BCD} \right)$. Biết tam giác $BCD$ vuông tại $C$ và $AB = \frac{{a\sqrt 6 }}{2},AC = a\sqrt 2 ,CD = a$. Gọi $E$ là trung điểm của $AD$. Tính góc giữa hai đường thẳng $AB$ và $CE?$

Lời giải

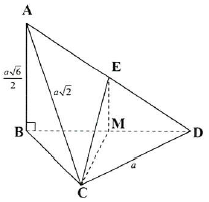
Ta có: $BC = \sqrt {A{C^2} – A{B^2}} = \frac{{a\sqrt 2 }}{2},BD = \frac{{a\sqrt 6 }}{2}$.

Gọi $M$ là trung điểm $BD \Rightarrow ME//AB$,

$ME = \frac{1}{2}AB = \frac{{a\sqrt 6 }}{4},CM = \frac{{BD}}{2} = \frac{{a\sqrt 6 }}{4}$

$ \Rightarrow \vartriangle CME$ vuông cân tại $M$.

Ta có $\left( {AB,CE} \right) = \left( {EM,CE} \right) = \widehat {CEM} = {45^ \circ }$.

Câu 24: Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với $AB$ và $AD,SA = a$. Gọi $M$ là trung điểm của $SB$. Tính góc giữa $AM$ và $BD$.

Lời giải

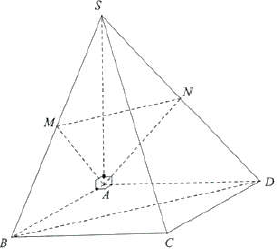
Gọi $N$ là trung điểm của $SD$ khi đó ta có $MN//BD \Rightarrow \left( {AM,BD} \right) = \left( {AM,MN} \right)$.

Theo giả thiết ta có: $AM = \frac{1}{2}SB = \frac{{a\sqrt 2 }}{2}$;

$AN = \frac{1}{2}SD = \frac{{a\sqrt 2 }}{2};MN = \frac{1}{2}BD = \frac{{a\sqrt 2 }}{2}$

$ \Rightarrow \vartriangle AMN$ đều $ \Rightarrow \widehat {AMN} = {60^ \circ }$. Vậy $\left( {AM,BD} \right) = {60^ \circ }$.

Câu 25: Cho hình chóp $S \cdot ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $I$ và $J$ lần lượt là trung điểm của $SC$ và $BC$. Số đo của góc $\left( {IJ,CD} \right)$ bằng?

Lời giải

Gọi $O$ là tâm của hình thoi $ABCD$

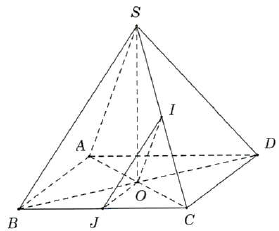
$ \Rightarrow OJ$ là đường trung bình của $\vartriangle BCD$. Suy ra $\left\{ {\begin{array}{*{20}{l}}
{OJ//CD} \\
{OJ = \frac{1}{2}CD}
\end{array}} \right.$.

Vì $CD//OJ \Rightarrow \left( {IJ,CD} \right) = \left( {IJ,OJ} \right)$.

Xét tam giác $IOJ$, có $\left\{ {\begin{array}{*{20}{l}}
{IJ = \frac{1}{2}SB = \frac{a}{2}} \\
{OJ = \frac{1}{2}CD = \frac{a}{2}} \\
{IO = \frac{1}{2}SA = \frac{a}{2}}
\end{array} \Rightarrow {\text{\Delta }}IOJ} \right.$ đều.

Vậy $\left( {IJ,CD} \right) = \left( {IJ,OJ} \right) = \widehat {IJO} = {60^ \circ }$.

II. DẠNG 2: CHỨNG MINH HAI ĐƯỜNG THẲNG VUÔNG GÓC

Phương pháp:

Hai đường thẳng $a,b$ được gọi là vuông góc với nhau, kí hiệu $a \bot b$, nếu góc giữa chúng bằng ${90^ \circ }$.

Câu 26: Cho tam giác $MNP$ vuông tại $N$ và một điểm $A$ nằm ngoài mặt phẳng $\left( {MNP} \right)$. Lần lượt lấy các điểm $B,C,D$ sao cho $M,N,P$ tương ứng là trung điểm của $AB,AC,CD$ (H.7.7).

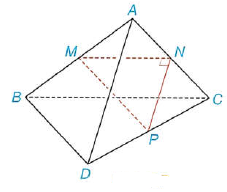
Chứng minh rằng $AD$ và $BC$ vuông góc với nhau và chéo nhau.

Lời giải

Vì $AD//NP,BC//MN$ và $\left( {MN,NP} \right) = {90^ \circ }$ nên $\left( {AD,BC} \right) = {90^ \circ } \Rightarrow AD \bot BC$.

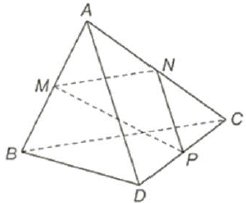
Nếu $D \in \left( {ABC} \right)$ thì $A \in \left( {MNP} \right)$ (vô lí).

Vậy $D \notin \left( {ABC} \right)$ nên $AD,BC$ chéo nhau.

Câu 27: Cho hình hộp $ABCD \cdot A’B’C’D’$ có các cạnh bằng nhau. Chứng minh rằng tứ diện $ACB’D’$ có các cặp cạnh đối diện vuông góc với nhau.

Lời giải

Vì $ABB’A’$ là hình thoi nên $AB’ \bot A’B$, mà $A’B//CD’ \Rightarrow AB’ \bot CD’$.

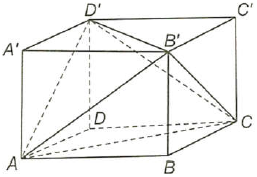
Tương tự cho các cặp còn lại.

Câu 28: Cho tứ diện $ABCD$ có $\widehat {CBD} = {90^ \circ }$.

a) Gọi $M,N$ tương ứng là trung điểm của $AB,AD$. Chứng minh rằng $MN$ vuông góc với $BC$.

b) Gọi $G,K$ tương ứng là trọng tâm của các tam giác $ABC,ACD$. Chứng minh rằng $GK$ vuông góc với $BC$.

a) Vì $MN//BD,BD \bot BC \Rightarrow MN \bot BC$.

Lời giải

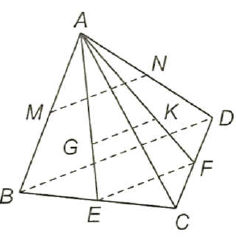
b) $GK//EF,EF//BD \Rightarrow GK//BD,BD \bot BC \Rightarrow GK \bot BC$.

Câu 29: Cho hình chóp $S.ABCD$ có đáy là hình bình hành, $SAB$ là tam giác cân tại $S$. Gọi $M$ là trung điểm $AB$ (Hình 3). Chứng minh rằng $SM \bot CD$.

Lời giải

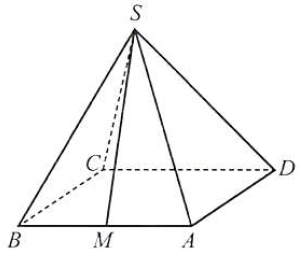
Vì $SA = SB,MA = MB$ nên $SM$ là đường trung trực của $AB$ trong $\left( {SAB} \right)$. Suy ra $SM \bot AB$.

Vì $ABCD$ là hình bình hành nên $AB//CD$.

Từ đó, suy ra $SM \bot CD$.

Câu 30: Cho hình hộp $ABCD \cdot A’B’C’D’$ có đáy là hình vuông.

a) Chứng minh rằng $AB \bot A’D’$ và $AC \bot B’D’$.

b) Tính góc giữa hai đường thẳng $AC$ và $A’B’$.

Lời giải

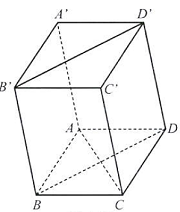
a) Vì $ABB’A’$ ‘ là hình bình hành nên $AB//A’B’$ ‘.

Do $A’B’C’D’$ là hình vuông nên $A’D’ \bot A’B’$.

Từ đó, suy ra $AB \bot A’D’$.

Vì $BDD’B’$ có $BB’//DD’$ và $BB’ = DD’$ nên $BDD’B’$ ‘à hình bình hành, suy ra $BD//B’D’$. Mà $AC \bot BD$ do $ABCD$ là hình vuông. Như vậy, ta có $AC \bot B’D’$.

b) Xét hình vuông $ABCD$ có

$\left( {AC,AB} \right) = \widehat {CAB} = {45^ \circ }$.

Mà $AB//A’B’$ nên $\left( {AC,A’B’} \right) = \left( {AC,AB} \right) = {45^ \circ }$.

Vậy góc giữa hai đường thẳng $AC$ và $A’B’$ bằng ${45^ \circ }$.

Câu 31: Cho hình lăng trụ $MNPQ \cdot M’N’P’Q’$ có tất cả các cạnh bằng nhau. Chứng minh rằng $M’N \bot P’Q$.

Lời giải

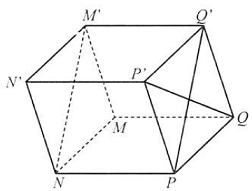
Vì $PQQ’P’$ là hình thoi (do các cạnh bằng nhau) nên $P’Q \bot PQ$ ‘.

Do $NP = MQ = M’Q’$ và $NP//MQ//M’Q’$ nên $NPQ’M’$ là hình bình hành, suy ra $M’N//PQ$ ‘.

Từ đó ta có $M’N \bot P’Q$.

Câu 32: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật tâm $O$ và tam giác $SAC$ vuông tại $S$. Gọi $M$ là trung điểm của cạnh $SB$. Chứng minh rằng đường thẳng $OM$ vuông góc với đường thẳng $SB$.

Lời giải.

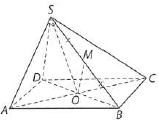
Ta có tam giác $SAC$ vuông tại $S$ và $O$ là trung điểm của $AC$ nên $SO = \frac{1}{2}AC$.

Ta lại có $ABCD$ là hình chữ nhật nên $AC = BD$,

suy ra $SO = \frac{1}{2}BD$, mà $O$ là trung điểm của $BD$

nên tam giác $SBD$ vuông tại $S$ hay $SD \bot SB$.

Vì $OM//SD$ và $SD \bot SB$ nên $OM \bot SB$.

Câu 33: Cho tứ diện $ABCD$, gọi $M$ và $N$ lần lượt là trung điểm của $AC$ và $BD$. Biết $MN = a\sqrt 3 ;AB = 2\sqrt 2 a$ và $CD = 2a$. Chứng minh rằng đường thẳng $AB$ vuông góc với đường thẳng $CD$.

Lời giải.

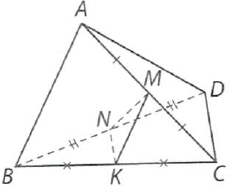
Lấy $K$ là trung điểm của cạnh ${\text{BC}}$, ta có: $NK$ và $MK$ lần lượt là đường trung bình của tam giác $BCD$ và tam giác $ABC$ nên $NK = a$ và $MK = a\sqrt 2 $.

Do đó, $M{N^2} = 3{a^2} = M{K^2} + N{K^2}$ suy ra tam giác $MNK$ vuông tại $K$, hay $MK \bot NK$ mà $MK//AB$ và $NK//CD$ nên $\left( {AB,CD} \right) = \left( {MK,NK} \right) = {90^ \circ }$, hay $AB \bot CD$.

Câu 34: Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh bằng $a$ và các cạnh bên đều bằng $a$. Gọi $M,N$ lần lượt là trung điểm của $AD,SD$. Chứng minh rằng $MN \bot SC$.

Lời giải

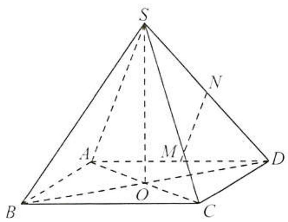
$\vartriangle SAD$ có $M,N$ lần lượt là trung điểm của $AD,SD$, suy ra $MN$ là đường trung bình của $\vartriangle SAD$, suy ra $MN//SA$.

Vậy $\left( {MN,SC} \right) = \left( {SA,SC} \right)$.

$\vartriangle ABC$ vuông tại $B$ nên $AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 $.

Xét $\vartriangle SAC$, nhận thấy: $A{C^2} = S{A^2} + S{C^2}$.

Theo định lí Pythagore đảo, $\vartriangle SAC$ vuông tại $S$.

Suy ra $\widehat {ASC} = {90^ \circ }$ hay $\left( {MN,SC} \right) = \widehat {ASC} = {90^ \circ }$.

Vậy $MN \bot SC$.

Câu 35: Cho tứ diện $ABCD$ có $AB = CD,AC = BD,AD = BC$.

a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với hai cạnh đó.

b) Chứng minh hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.

Lời giải

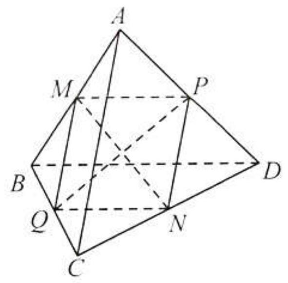
a) Gọi $M,N,P,Q$ lần lượt là trung điểm của các canh $AB,CD,AD,BC$.

Ta có $\vartriangle ACD = \vartriangle BDC$ (c.c.c), suy ra $AN = BN$, suy ra $\vartriangle NAB$ cân tại $N$. Mà $M$ là trung điểm của $AB$, suy ra $NM \bot AB$.

Tương tự ta có $NM \bot CD$.

b) Ta có $MQ = PN = \frac{{AC}}{2},MP = QN = \frac{{BD}}{2},AC = BD$.

Suy ra $MQ = PN = MP = QN$.

Vậy tứ giác $MPNQ$ là hình thoi, suy ra $MN \bot PQ$.

Câu 36: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $BCD$.

Chứng minh hai đường thẳng $OA$ và $CD$ vuông góc với nhau.

Lời giải

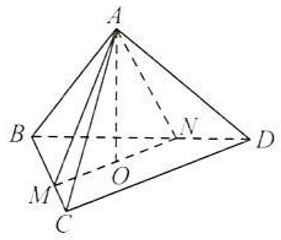
Qua $O$ vẽ đường $MN//CD\left( {M \in BC,N \in BD} \right)$.

Ta có $OM = ON,AM = AN$, suy ra $\vartriangle AMN$ cân tại $A$, suy ra $AO \bot MN$. Mà $MN//CD$ nên $AO \bot CD$.

Câu 37: Cho tứ diện $ABDC$ có $AB = AC$ và $DB = DC$. Chứng minh: $BC \bot AD$.

Lời giải

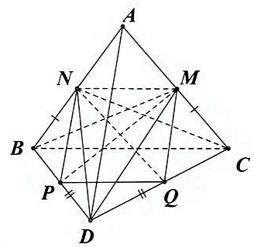
Gọi $M,N,P,Q$ lần lượt là trung điểm của $AC,AB,BD,CD$.

Dễ dàng chứng minh được $MNPQ$ là hình bình hành.

Dễ dàng chứng minh được $\vartriangle MBD = \vartriangle NCD\left( {{\text{c}} – {\text{c}} – {\text{c}}} \right)$.

Suy ra hai trung tuyến tương ứng $NQ = MP$.

Suy ra $MNPQ$ là hình chữ nhật $ \Rightarrow MN \bot MQ$. Mà $AD//MQ$ và $BC//MN$ nên $AD \bot BC$.

Câu 38: Trong hình hộp $ABCD \cdot A’B’C’D’$ có tất cả các cạnh đều bằng nhau. Chứng minh:

a) $A’C’ \bot BD$.

b) $A’B \bot DC’$.

c) $BC’ \bot A’D$.

Lời giải

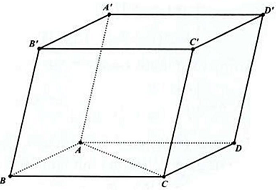
Vì hình hộp $ABCD \cdot A’B’C’D’$ có tất cả các cạnh đều bằng nhau nên các tứ giác $ABCD$, $A’B’BA,B’C’CB$ đều là hình thoi.

$AC \bot BD$ mà $AC//A’C’ \Rightarrow A’C’ \bot BD$.

$A’B \bot AB’$ mà $AB’//DC’ \Rightarrow A’B \bot DC’$.

$BC’ \bot B’C$ mà $B’C//A’D \Rightarrow BC’ \bot A’D$.

III. DẠNG 3: BÀI TOÁN THỰC TẾ

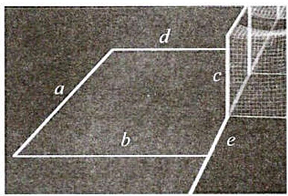
Câu 39: Hình 5 gợi nên hình ảnh một số cặp đường thẳng vuông góc với nhau. Hãy chỉ ra ba cặp đường thẳng vuông góc với nhau.

Lời giải

Ba cặp đường thẳng vuông góc có thể là $a$ và $b;b$ và $c;c$ và $d$.

Câu 40: Đối với nhà gỗ truyền thống, trong các cấu kiện: hoành, quá giang, xà cái, rui, cột tương ứng được đánh số $1,2,3,4,5$ như trong Hình 7.8 , những cặp cấu kiện nào vuông góc với nhau?

Lời giải

Những cặp đường thẳng sau vuông góc với nhau: hoành (1) và quá giang (2); hoành (1) và rui (4); hoành (1) và cột (5); quá giang (2) và xà cái (3); quá giang (2) và cột (5); xà cái (3) và rui (4); xà cái (3) và cột (5).

Câu 41: Kim tự tháp Kheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng $230{\text{\;m}}$, các cạnh bên bằng nhau và dài khoảng $219m$ (kích thước hiện nay). (Theo britannica.com). Tính (gần đúng) góc tạo bởi cạnh bên $SC$ và cạnh đáy $AB$ của kim tự tháp (H.7.4).

Lời giải

Gọi $H$ là trung điểm của $CD$ thì $CH = 115{\text{\;m}}$.

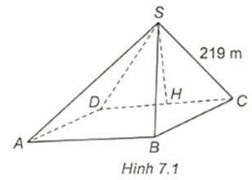
Vì $DC//AB$ nên $\left( {SC;AB} \right) = \left( {SC;CD} \right) = \widehat {SCH}$.

Ta có: ${\text{cos}}\widehat {SCH} = \frac{{CH}}{{SC}} = \frac{{115}}{{219}} \Rightarrow \widehat {SCH} \approx 58,{3^ \circ }$.

Câu 42: Tháp Phước Duyên ở Chùa Thiên Mụ (Huế) cao bảy tầng, sàn của mỗi tầng đều là hình bát giác đều. Hãy tính góc giữa hai cạnh $AB$ và $CD$ được thể hiện trên hình sau:

Lời giải.

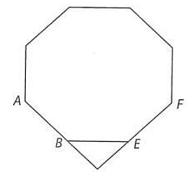
Ta có: $CD//EF$ nên $\left( {AB,CD} \right) = \left( {AB,EF} \right)$, với $AB,EF$ là hai cạnh của một hình bát giác đều.

Góc ngoài của một bát giác đều bằng $\frac{{{{360}^ \circ }}}{8} = {45^ \circ }$ nên $\left( {AB,EF} \right) = {90^ \circ }$, suy ra $\left( {AB,CD} \right) = {90^ \circ }$.

Câu 43: Một chiếc thang có dạng hình thang cân cao $6{\text{\;m}}$, hai chân thang cách nhau $80{\text{\;cm}}$, hai ngọn thang cách nhau $60{\text{\;cm}}$. Thang được dựa vào bờ tường như hình bên. Tính góc tạo giữa đường thẳng chân tường và cạnh cột thang (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai).

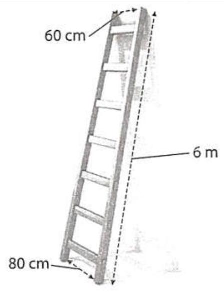
Lời giải

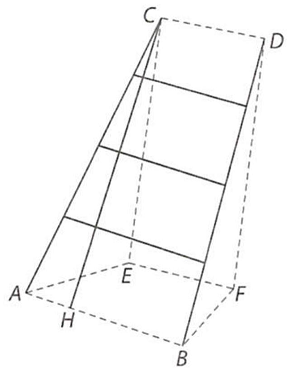
Gọi $A,B$ là hai điểm tại hai vị trí chân thang và $C,D$ là hai điểm tại hai vị trí ngọn thang, $EF$ là đường chân tường.

Ta có $EF//AB$ nên $\left( {EF,AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}$.

Kẻ $CH$ vuông góc với $AB$ tại $H$, khi đó

$AH = \frac{{AB – CD}}{2} = 10\left( {{\text{\;cm}}} \right) = 0,1\left( {{\text{\;m}}} \right)$. Tam giác $ACH$ vuông tại $H$ nên

${\text{cos}}\widehat {CAH} = \frac{{AH}}{{AC}} = \frac{{0,1}}{6} = \frac{1}{{60}}$,

suy ra $\widehat {CAH} \approx 89,{05^ \circ }$.

Vậy góc tạo giữa đường thẳng chân tường và cạnh cột thang bằng khoảng $89,{05^ \circ }$.