Các Dạng Toán Bài Phép Chiếu Vuông Góc-Góc Giữa Đường Thẳng Và Mặt Phẳng

Các dạng toán bài Phép chiếu vuông góc-Góc giữa đường thẳng và mặt phẳng giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
DẠNG 1. XÁC ĐỊNH GÓC GIỮA ĐƯỜNG THẲNG VỚI MẶT PHẲNG

Phương pháp:

Để tìm góc giữa đường thẳng $a$ và mặt phẳng $(P)$ ta tìm hình chiếu vuông góc $a’$ của $a$ lên $(P)$. Khi đó, $\left( {\widehat {a,\,(P)}} \right) = \left( {a,\,a’} \right)$.

Nhận xét: Cho điểm $A$ có hình chiếu $H$ trên mặt phẳng $\left( P \right)$. Lấy điểm $O$ thuộc mặt phẳng $\left( P \right),O$ không trùng $H$. Khi đó góc giữa đường thẳng $AO$ và mặt phẳng $\left( P \right)$ bằng góc $AOH$

Câu 1. Cho hình chóp $S.ABC$ có $SA = SB = SC$. Gọi $O$ là hình chiếu của $S$ trên mặt phẳng $\left( {ABC} \right)$.

a) Chứng minh rằng $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$.

b) Xác định hình chiếu của đường thẳng $SA$ trên mặt phẳng $\left( {ABC} \right)$.

c) Chứng minh rằng nếu $AO \bot BC$ thì $SA \bot BC$.

d) Xác định hình chiếu của các tam giác $SBC,SCA,SAB$ trên mặt phẳng $\left( {ABC} \right)$.

Lời giải

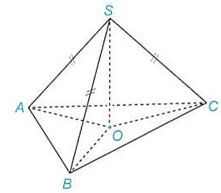
a) Do $SO \bot \left( {ABC} \right)$ và $SA = SB = SC$ nên $\vartriangle SOA = \vartriangle SOB = \vartriangle SOC \Rightarrow OA = OB = OC$.

b) Hình chiếu của $SA$ trên mặt phẳng $\left( {ABC} \right)$ là $OA$.

C) Do $SO \bot \left( {ABC} \right)$ nên $SO \bot BC$, mà $AO \bot BC$ suy ra $BC \bot \left( {SOA} \right)$. Do đó $BC \bot SA$.

d) Hình chiếu của mỗi tam giác $SBC,SCA,SAB$ trên mặt phẳng $\left( {ABC} \right)$ lần lượt là tam giác $OBC,OCA,OAB$.

Câu 2. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, tam giác $ABC$ vuông tại $B$.

a) Xác định hình chiếu của điểm $S$ trên mặt phẳng $\left( {ABC} \right)$.

b) Xác định hình chiếu của tam giác $SBC$ trên mặt phẳng $\left( {ABC} \right)$.

c) Xác định hình chiếu của tam giác $SBC$ trên mặt phẳng $\left( {SAB} \right)$.

Lời giải

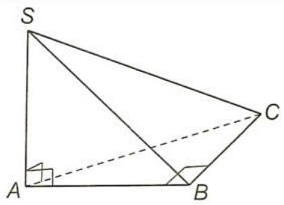
a) Hình chiếu của $S$ trên $\left( {ABC} \right)$ là điểm $A$.

b) Hình chiếu của tam giác $SBC$ trên $\left( {ABC} \right)$ là tam giác $ABC$.

c) Hình chiếu của tam giác $SBC$ trên $\left( {SAB} \right)$ là đoạn thẳng $SB$ vì $CB \bot \left( {SAB} \right)$.

Câu 3. Cho hình chóp $S.ABCD$ có đáy là hình vuông $ABCD$ cạnh $a,SA \bot \left( {ABCD} \right)$ và $SA = a\sqrt 2 $.

a) Tính góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$.

b) Tính góc giữa $BD$ và mặt phẳng $\left( {SAC} \right)$.

c) Tìm hình chiếu của $SB$ trên mặt phẳng $\left( {SAC} \right)$.

Lời giải

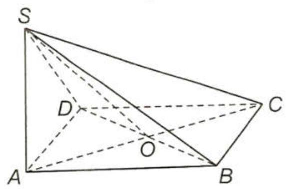
a) Vi $AC = a\sqrt 2 ,SA = AC = a\sqrt 2 \Rightarrow \widehat {SCA} = {45^ \circ }$. Vậy góc giữa $SC$ và $\left( {ABCD} \right)$ bằng ${45^ \circ }$.

b) Vi $BD \bot AC,BD \bot SA \Rightarrow BD \bot \left( {SAC} \right)$. Vậy góc giữa $BD$ và $\left( {SAC} \right)$ bằng ${90^ \circ }$.

c) Gọi $O$ là giao điểm của $AC$ và $BD$. Hình chiếu của $SB$ trên mặt phẳng $\left( {SAC} \right)$ là $SO$.

Câu 4. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, tam giác $ABC$ vuông tại $B,SA = AB = BC = a$.

a) Xác định hình chiếu của $A$ trên mặt phẳng $\left( {SBC} \right)$.

b) Tính góc giữa $SC$ và mặt phẳng $\left( {ABC} \right)$.

Lời giải

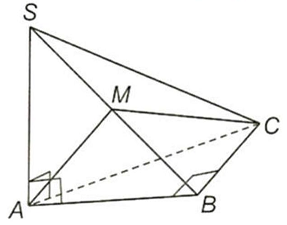
a) Vì $BC \bot AB,BC \bot SA$ nên

$BC \bot \left( {SAB} \right),AM \bot SB$ tại $M \Rightarrow AM \bot \left( {SBC} \right)$.

Hình chiếu của $A$ trên mặt phẳng $\left( {SBC} \right)$ là $M$.

b) Góc giữa $SC$ và $\left( {ABC} \right)$ bằng góc $SCA$.

Ta có: $AC = a\sqrt 2 \Rightarrow tan\widehat {SCA} = \frac{{SA}}{{AC}} = \frac{1}{{\sqrt 2 }}$.

Do đó $\widehat {SCA} = {45^ \circ }$.

Câu 5. Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều cạnh bằng $3a$, các cạnh bên $SA,SB,SC$ bằng nhau và bằng $2a\sqrt 3 $. Tính góc giữa đường thẳng $SA$ và mặt phẳng $\left( {ABC} \right)$.

Lời giải

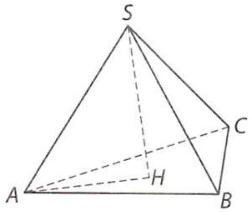
Gọi $H$ là hình chiếu của $S$ trên mặt phẳng $\left( {ABC} \right)$, khi đó các tam giác $SHA,SHB,SHC$ là những tam giác vuông tại $H$.

Theo định lí Pythagore, ta có: $HA = HB = HC$, do đó $H$ là tâm của tam giác đều $ABC$. Ta tính được $AH = a\sqrt 3 $.

Vì $AH$ là hình chiếu của $SA$ trên mặt phẳng $\left( {ABC} \right)$ nên góc giữa $SA$ và mặt phẳng $\left( {ABC} \right)$ bằng góc giữa đường thẳng $SA$ và đường thẳng $AH$.

Xét tam giác $SAH$ vuông tại $H$, ta có: $cos\widehat {SAH} = \frac{{AH}}{{SA}} = \frac{1}{2}$, suy ra $\widehat {SAH} = {60^ \circ }$.

Vậy góc giữa $SA$ và mặt phẳng $\left( {ABC} \right)$ bằng ${60^ \circ }$.

Câu 6. Cho hình lăng trụ tam giác $ABC \cdot A’B’C’$ có đáy là tam giác $ABC$ cân tại $A$, góc $BAC$ bằng ${120^ \circ }$ và $AB = 2a$. Hình chiếu của $A’$ trên mặt phẳng $\left( {ABC} \right)$ trùng với trung điểm $H$ của $BC$, biết $AA’ = a\sqrt 2 $. Tính góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {ABC} \right)$.

Lời giải

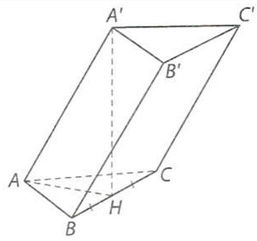
Ta có: $AH$ là hình chiếu của $AA’$ trên mặt phẳng $\left( {ABC} \right)$ và tam giác $AA’H$ vuông tại $H$. Do đó, góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {ABC} \right)$ bằng góc giữa hai đường thẳng $AA’$ và $AH$.

Xét tam giác $ABH$ vuông tại $H$, có: $\widehat {HAB} = \frac{1}{2}\widehat {BAC} = {60^ \circ }$, suy ra $AH = a$.

Xét tam giác $AA’H$ vuông tại $H$, có: $cos\widehat {HAA’} = \frac{{AH}}{{AA’}} = \frac{1}{{\sqrt 2 }}$, suy ra $\widehat {HAA’} = {45^ \circ }$.

Do đó $\left( {AA’,AH} \right) = {45^ \circ }$, hay góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {ABC} \right)$ bằng ${45^ \circ }$.

Câu 7. Cho tứ diện $ABCD$ có tất cả các cạnh bằng nhau và bằng $a$. Tính côsin của góc giữa đường thẳng $AB$ và mặt phẳng $\left( {BCD} \right)$.

Lời giải

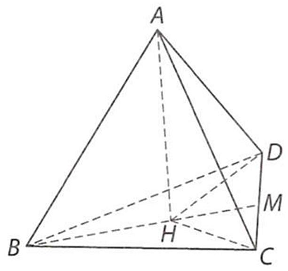
Kẻ $AH \bot \left( {BCD} \right)$ tại $H$, ta có $BH$ là hình chiếu vuông góc của $AB$ trên mặt phẳng $\left( {BCD} \right)$ nên góc giữa đường thẳng $AB$ và mặt phẳng $\left( {BCD} \right)$ bằng góc giữa hai đường thẳng $AB$ và $BH$, mà $\left( {AB,BH} \right) = \widehat {ABH}$.

Vì $AB = AC = AD$ nên $HD = HB = HC$, hay $H$ là tâm của tam giác $BCD$, suy ra $BH = \frac{{a\sqrt 3 }}{3}$.

Từ đó ta tính được: $cos\widehat {ABH} = \frac{{BH}}{{AB}} = \frac{{\sqrt 3 }}{3}$.

Vậy côsin của góc giữa đường thẳng $AB$ và mặt phẳng $\left( {BCD} \right)$ bằng $\frac{{\sqrt 3 }}{3}$.

Câu 8. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a,SA \bot \left( {ABCD} \right)$, $SA = a\sqrt 2 $.

a) Tính góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$.

b) Tính tang của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$.

Lời giải

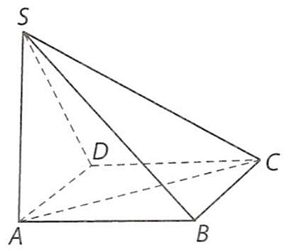
a) Vì $SA \bot \left( {ABCD} \right)$ nên $AC$ là hình chiếu vuông góc của $SC$ trên mặt phẳng $\left( {ABCD} \right)$, do đó góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng góc giữa hai đường thẳng $SC$ và $AC$, mà $\left( {SC,AC} \right) = \widehat {SCA}$. Vì tam giác $SAC$ vuông cân tại $A$ nên $\widehat {SCA} = {45^ \circ }$. Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng ${45^ \circ }$.

b) Ta có: $BC \bot AB,BC \bot SA$ nên $BC \bot \left( {SAB} \right)$, suy ra $SB$ là hình chiếu vuông góc của $SC$ trên mặt phẳng $\left( {SAB} \right)$, góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng góc giữa hai đường thẳng $SC$ và $SB$.

Ta có: $\left( {SB,SC} \right) = \widehat {BSC}$.

Xét tam giác $SBC$ vuông tại $B$, có:

$SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 3 ,BC = a$.

Do đó, $tan\widehat {BSC} = \frac{{BC}}{{SB}} = \frac{{\sqrt 3 }}{3}$.

Vậy tang của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng $\frac{{\sqrt 3 }}{3}$.

Câu 9. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, đáy là tam giác $ABC$ vuông cân tại $B$, biết $AB = a,SA = a\sqrt 6 $.

a) Tính tang của góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$.

b) Tính sin của góc giữa đường thẳng $AC$ và mặt phẳng $\left( {SBC} \right)$.

Lời giải

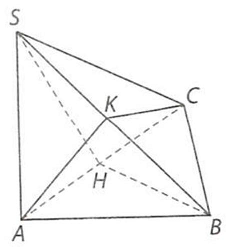
a) Kẻ $BH \bot AC$ tại $H$, mà $SA \bot \left( {ABC} \right)$ nên $SA \bot BH$, suy ra $BH \bot \left( {SAC} \right)$. Do đó, $SH$ là hình chiếu vuông góc của $SB$ trên mặt phẳng $\left( {SAC} \right)$ nên góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$ bằng góc giữa hai đường thẳng $SB$ và $SH$, mà $\left( {SB,SH} \right) = \widehat {BSH}$.

Ta tính được: $BH = \frac{{a\sqrt 2 }}{2},SH = \frac{{a\sqrt {26} }}{2}$,

suy ra $tan\widehat {BSH} = \frac{{BH}}{{SH}} = \frac{{\sqrt {13} }}{{13}}$.

b) Kẻ $AK \bot SB$ tại $K$, mà $BC \bot \left( {SAB} \right)$ nên $BC \bot AK$, suy ra $AK \bot \left( {SBC} \right)$. Do đó $CK$ là hình chiếu vuông góc của $AC$ trên $\left( {SBC} \right)$, suy ra góc giữa đường thẳng $AC$ và $\left( {SBC} \right)$ bằng góc giữa hai đường thẳng $AC$ và $CK$, mà $\left( {AC,CK} \right) = \widehat {ACK}$.

Ta có: $AK = \frac{{SA \cdot AB}}{{SB}} = a\sqrt {\frac{6}{7}} $, suy ra $sin\widehat {ACK} = \frac{{AK}}{{AC}} = \sqrt {\frac{3}{7}} $.

Câu 10. Cho hình hộp $ABCD \cdot A’B’C’D’$ có đáy $ABCD$ là hình vuông cạnh a và $AA’ = a\sqrt 2 $, hình chiếu vuông góc của $A$ trên mặt phẳng $\left( {A’B’C’D’} \right)$ trùng với trung điểm của $B’D’$. Tính góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {A’B’C’D’} \right)$.

Lời giải

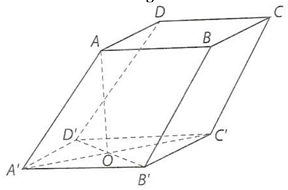
Gọi $O$ là giao điểm của $A’C’$ và $B’D’$. Ta có: $A’O$ là hình chiếu vuông góc của $AA’$ trên mặt phẳng $\left( {A’B’C’D’} \right)$, góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {A’B’C’D’} \right)$ bằng góc giữa $AA’$ và $A’O$.

Mà $\left( {AA’,A’O} \right) = \widehat {AA’O}$, ta lại có $A’O = \frac{{a\sqrt 2 }}{2}$. Do đó $cos\widehat {AA’O} = \frac{{OA’}}{{AA’}} = \frac{1}{2}$, suy ra $\widehat {AA’O} = {60^ \circ }$.

Vậy góc giữa đường thẳng $AA’$ và mặt phẳng $\left( {A’B’C’D’} \right)$ bằng ${60^ \circ }$.

Câu 11. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$ và các cạnh đều bằng $a$.

a) Chứng minh rằng $SO \bot \left( {ABCD} \right)$.

b) Tính góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBD} \right)$.

c) Gọi $M$ là trung điểm của cạnh $SC$ và $\alpha $ là góc giữa đường thẳng $OM$ và mặt phẳng $\left( {SBC} \right)$. Tính $sin\alpha $.

Lời giải

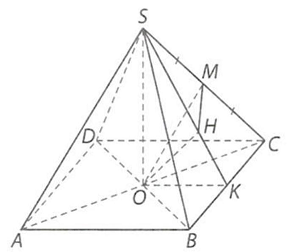
a) Ta có: $SO \bot AC$; $SO \bot BD$ nên $SO \bot \left( {ABCD} \right)$.

b) Vì $AO \bot \left( {SBD} \right)$ nên $SO$ là hình chiếu vuông góc của $SA$ trên mặt phẳng $\left( {SBD} \right)$, do đó góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBD} \right)$ bằng góc giữa hai đường thẳng $SA$ và $SO$.

Mà $\left( {SA,SO} \right) = \widehat {ASO}$ nên góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBD} \right)$ bằng góc $ASO$.

Xét tam giác $SAC$ có $S{A^2} + S{C^2} = A{C^2}$ và $SA = SC$ nên tam giác $SAC$ vuông cân tại $S$, suy ra $\widehat {ASO} = {45^ \circ }$.

Vậy góc giữa đường thẳng $SA$ và mặt phẳng $\left( {SBD} \right)$ bằng ${45^ \circ }$.

c) Kẻ $OK \bot BC$ tại $K,OH \bot SK$ tại $H$ thì ta chứng minh được $OH \bot \left( {SBC} \right)$, suy ra $HM$ là hình chiếu vuông góc của $OM$ trên mặt phẳng $\left( {SBC} \right)$, do đó góc giữa đường thẳng $OM$ và mặt phẳng $\left( {SBC} \right)$ bằng góc giữa hai đường thẳng $OM$ và $MH$, mà $\left( {OM,MH} \right) = \widehat {OMH}$ nên góc giữa đường thẳng $OM$ và mặt phẳng $\left( {SBC} \right)$ bằng góc $OMH$ hay $\widehat {OMH} = \alpha $.

Ta có: $OM = \frac{a}{2},OK = \frac{a}{2},SO = \frac{{a\sqrt 2 }}{2}$.

Tam giác SOK vuông tại $O$, đường cao $OH$ nên $OH = \frac{{SO \cdot OK}}{{SK}} = \frac{{a\sqrt 6 }}{6}$.

Vì tam giác $OMH$ vuông tại $H$ nên $sin\alpha = sin\widehat {OMH} = \frac{{OH}}{{OM}} = \frac{{\sqrt 6 }}{3}$.

Câu 12. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông và $SA \bot \left( {ABCD} \right)$.

Gọi $H,I,K$ lần lượt là hình chiếu vuông góc của điểm $A$ trên các cạnh $SB,SC$ và $SD$. Chứng minh rằng:

a) $BC \bot $ ( $SAB$ ), $CD \bot $ ( $SAD$ ), $BD \bot \left( {SAC} \right)$.

b) $SC \bot \left( {AHK} \right)$ và điểm $I$ thuộc mặt phẳng $\left( {AHK} \right)$.

c) $HK \bot \left( {SAC} \right)$ và $HK \bot AI$.

Lời giải

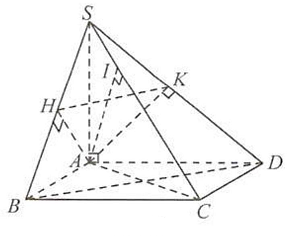
a) Ta có $BC \bot AB$ (vì $ABCD$ là hình vuông) và $SA \bot BC$ (vì $SA \bot \left( {ABCD} \right)$ ), suy ra $BC \bot \left( {SAB} \right)$.

Ta có $CD \bot AD$ (vì $ABCD$ là hình vuông) và $SA \bot CD$ (vì $SA \bot \left( {ABCD} \right)$ ), suy ra $CD \bot \left( {SAD} \right)$.

Ta có $BD \bot AC$ (vì $ABCD$ là hình vuông) và $SA \bot BD$ (vì $SA \bot \left( {ABCD} \right)$ ), suy ra $BD \bot \left( {SAC} \right)$.

b) Ta có $BC \bot \left( {SAB} \right)$ và $AH \subset \left( {SAB} \right)$, suy ra $BC \bot AH$. Mặt khác $AH \bot SB$, suy ra $AH \bot \left( {SBC} \right)$, suy ra $AH \bot SC$.(1)

Tương tự ta có $AK \bot CD$ và $AK \bot SD$, suy ra $AK \bot \left( {SCD} \right)$, suy ra $AK \bot SC$. (2)

Từ (1) và (2) suy ra $SC \bot \left( {AHK} \right)$.

Ta có $SC \bot \left( {AHK} \right)$ và $AI \bot SC$, suy ra $I \in \left( {AHK} \right)$.

c) Ta có $SA \bot \left( {ABCD} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{SA \bot AB} \\
{SA \bot AD}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\widehat {SAB} = {{90}^ \circ }} \\
{\widehat {SAD} = {{90}^ \circ }}
\end{array}} \right.} \right.$

Xét $\vartriangle SAB$ và $\vartriangle SAD$, ta có:

SA là cạnh chung;

$\widehat {SAB} = \widehat {SAD} = {90^ \circ }$

$AB = AD$.

Suy ra $\vartriangle SAB = \vartriangle SAD$ (c.g.c),

suy ra $SB = SD,SH = SK$.

Suy ra $\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}}$.

Vậy $HK//BD$.

Theo câu a) ta có $BD \bot \left( {SAC} \right)$, suy ra $HK \bot \left( {SAC} \right)$.

Ta lại có $AI \subset \left( {SAC} \right)$, suy ra $HK \bot AI$.

Câu 13. Cho tứ diện $ABCD$ có $AB \bot CD$ và $AC \bot BD$. Gọi $H$ là hình chiếu vuông góc của $A$ xuống mặt phẳng $\left( {BCD} \right)$. Chứng minh rằng $H$ là trực tâm của $\vartriangle BCD$ và $AD \bot BC$.

Lời giải

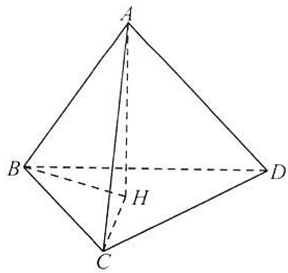
Ta có $CD \bot AB$ và $CD \bot AH$, suy ra $CD \bot \left( {ABH} \right)$, suy ra $CD \bot BH$.

Tương tự ta cũng có $BD \bot CH$.

Vậy $H$ là trực tâm của $\vartriangle BCD$.

Ta có $H$ là trực tâm của $\vartriangle BCD$, suy ra $BC \bot DH$. Ta lại có $BC \bot AH$, suy ra $BC \bot \left( {AHD} \right)$, suy ra $BC \bot AD$.

Câu 14. Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right),AB \bot AD,SA = AD = a\sqrt 3 ,AB = a$. Tính số đo của:

a) Góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABCD} \right)$.

b) Góc giữa đường thẳng $SD$ và mặt phẳng $\left( {SAB} \right)$.

Lời giải

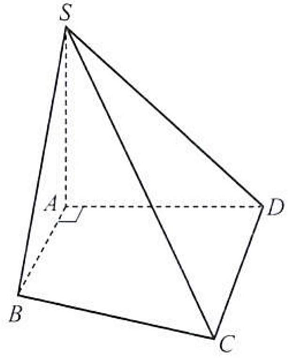
a) Vì $SA \bot \left( {ABCD} \right)$ nên $AB$ là hình chiếu của $SB$ trên $\left( {ABCD} \right)$. Suy ra góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABCD} \right)$ bằng góc giữa $SB$ và $AB$, hay bằng $\widehat {SBA}$.

Trong tam giác vuông $SAB$ có $tan\widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 $ nên $\widehat {SBA} = {60^ \circ }$.

Suy ra góc giữa đường thẳng $SB$ và mặt phẳng $\left( {ABCD} \right)$ bằng ${60^ \circ }$.

b) Vì $SA \bot \left( {ABCD} \right)$ và $AD \subset \left( {ABCD} \right)$ nên $SA \bot AD$. Mà $AD \bot AB$ và $SA,AB$ cắt nhau trong mặt phẳng $\left( {SAB} \right)$ nên $AD \bot \left( {SAB} \right)$. Suy ra $SA$ là hình chiếu của $SD$ trên $\left( {SAB} \right)$, khi đó góc giữa đường thẳng $SD$ và mặt phẳng $\left( {SAB} \right)$ bằng góc giữa $SD$ và $SA$, hay bằng $\widehat {DSA}$. Vì tam giác $DSA$ vuông cân tại $A$ nên $\widehat {DSA} = {45^ \circ }$. Vậy góc giữa đường thẳng $SD$ và mặt phẳng $\left( {SAB} \right)$ bằng ${45^ \circ }$.

DẠNG 2. ỨNG DỤNG

Câu 15. Tâm Trái Đất chuyển động quanh Mặt Trời theo quỹ đạo là một đường elip nhận tâm Mặt Trời làm tiêu điểm. Trong quá trình chuyển động, Trái Đất lại quay quanh trục Bắc Nam. Trục này có phương không đổi và luôn tạo với mặt phẳng chứa quỹ đạo một góc khoảng $66,{5^ \circ }$. (Theo nationalgeographic.org).

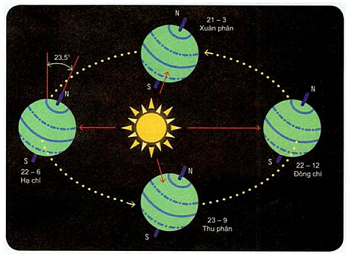
a) Giải thích vì sao hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo $\left( P \right)$ cũng có phương không đổi.

b) Giải thích vì sao có hai thời điểm trong năm mà tại đó hình chiếu của trục Trái Đất trên mặt phẳng $\left( P \right)$ thuộc đường thẳng nối tâm Mặt Trời và tâm Trái Đất.

Lời giải

a) Gọi $a,b$ là hai vị trí của trục Trái Đất, $a//b$. Gọi $a’,b’$ tương ứng là hình chiếu của $a,b$ trên $\left( P \right)$. Hai mặt phẳng $\left( {a,a} \right)$ và $\left( {b,b’} \right)$ chứa hai phương tương ứng song song với nhau đó là các phương cùng vuông góc với $\left( P \right)$ (phương chiếu) và $a//b$. Vì vậy, hai mặt phẳng $\left( {a,a’} \right)$ và $\left( {b,b’} \right)$ song song với nhau hoặc trùng nhau. Do đó, hai giao tuyến của chúng với $\left( P \right)$ là $a’$ và $b’$ cũng song song hoặc trùng nhau.

Lưu ý. Kết luận ở câu a thực chất được rút ra từ tính chất sau của phép chiếu song song: Phép chiếu song song biến hai đường thẳng song song có phương khác phương chiếu thành hai đường thẳng song song hoặc trùng nhau.

b) Hình chiếu của trục Trái Đất lên mặt phẳng $\left( P \right)$ có phương cố định. Gọi $m$ là đường thẳng đi qua tâm Mặt Trời và có phương cố định nói trên. Khi đó, hình chiếu của trục Trái Đất xuống $\left( P \right)$ thuộc đường thẳng $m$ khi và chỉ khi tâm Trái Đất ở vị trí là giao của $m$ với đường elip quỹ đạo của Trái Đất. Như vậy có hai vị trí thuộc quỹ đạo, ứng với hai thời điểm trong năm mà hình chiếu của trục Trái Đất trên $\left( P \right)$ thuộc đường thẳng $m$ (nối tâm Trái Đất và tâm Mặt Trời).

Câu 16. Cho điểm $S$ nằm ngoài mặt phẳng $\left( P \right)$, có hình chiếu $H$ trên $\left( P \right)$. Với mỗi điểm $M$ bất kì (không trùng $H$ ) trên mặt phẳng $\left( P \right)$, ta gọi đoạn thẳng $SM$ là đường xiên, đoạn thẳng $HM$ là hình chiếu trên $\left( P \right)$ của đường xiên đó. Chứng minh rằng:

a) Hai đường xiên $SM$ và $SM’$ bằng nhau khi và chỉ khi hai hình chiếu $HM$ và $HM’$ tương ứng của chúng bằng nhau;

b) Đường xiên $SM$ lớn hơn đường xiên $SM’$ nếu hình chiếu $HM$ lớn hơn hình chiếu $HM’$.

Lời giải

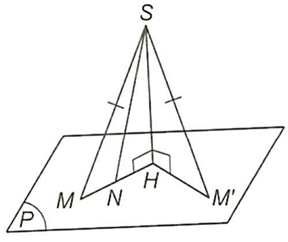
a) $\DeltaSHM = \DeltaSHM’ \Rightarrow HM = HM’$.

b) Trên tia $HM$ lấy điểm $N$ sao cho $SN = SM’$

$ \Rightarrow HN = HM’$ mà $SM > SM’ \Rightarrow SM > SN$

$ \Rightarrow HM > HN \Rightarrow HM > HM’$.

Câu 17. Trong một khoảng thời gian đầu kể từ khi cất cánh, máy bay bay theo một đường thẳng. Góc cất cánh của nó là góc giữa đường thẳng đó và mặt phẳng nằm ngang nơi cất cánh. Hai máy bay cất cánh và bay thẳng với cùng độ lớn vận tốc trong 5 phút đầu, với các góc cất cánh lần lượt là ${10^ \circ },{15^ \circ }$. Hỏi sau 1 phút kể từ khi cất cánh, máy bay nào ở độ cao so với mặt đất (phẳng, nằm ngang) lớn hơn?

Chú ý. Độ cao của máy bay so với mặt đất là khoảng cách từ máy bay (coi là một điểm) đến hình chiếu của nó trên mặt đất.

Lời giải

Vì $AM = A’M’,BM = AM \cdot sin{10^ \circ } < A’M’ \cdot sin{15^ \circ } = B’M’$.

Câu 18. Hãy nêu cách đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm.

Chú ý. Góc giữa đường thẳng chứa tia sáng mặt trời lúc giữa trưa với mặt phẳng nằm ngang tại vị trí đó được gọi là góc Mặt Trời. Giữa trưa là thời điểm ban ngày mà tâm Mặt Trời thuộc mặt phẳng chứa kinh tuyến đi qua điểm đang xét. Góc Mặt Trời ảnh hưởng tới sự hấp thụ nhiệt từ Mặt Trời của Trái Đất, tạo nên các mùa trong năm trên Trái Đất.

Lời giải

Lấy một cột $AB$, bóng của cột $AB$ là $AM$.

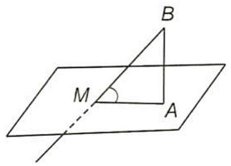
Khi đó $tan\widehat {BAM} = \frac{{AB}}{{AM}}$.

Từ đó tính được góc $\widehat {BAM}$.

Câu 19. Một chiếc cột cao $3m$ được dựng vuông góc với mặt đất phẳng. Dưới ánh nắng mặt trời, bóng của cột trên mặt đất dài $5\;m$. Tính góc giữa đường thẳng chứa tia nắng mặt trời và mặt đất (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải

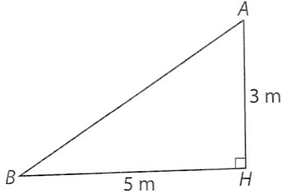
Góc giữa tia nắng mặt trời $AB$ và mặt đất là góc $ABH$. Ta có: $tan\widehat {ABH} = \frac{{AH}}{{BH}} = \frac{3}{5}$, suy ra $\widehat {ABH} \approx 30,{96^ \circ }$.

Câu 20. Một con diều được thả với dây căng, tạo với mặt đất một góc ${60^ \circ }$. Đoạn dây diều (từ đầu ở mặt đất đến đầu ở con diều) dài $10\;m$. Hỏi hình chiếu vuông góc trên mặt đất của con diều cách đầu dây diều trên mặt đất bao nhiêu centimét (lấy giá trị nguyên gần đúng)?

Lời giải

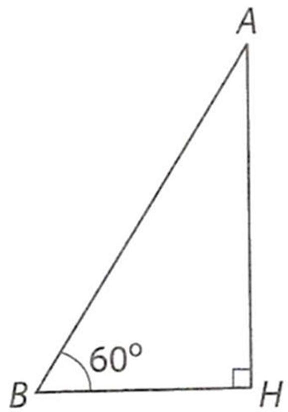
Gọi $A$ là vị trí con diều, $B$ là vị trí đầu dây diều trên mặt đất, $H$ là hình chiếu vuông góc của $A$ trền mặt đất.

Tam giác $ABH$ vuông tại $H$, góc $ABH$ bằng ${60^ \circ }$ và $AB = 10\;m = 1000\;cm$.

Ta có: $AH = AB \cdot sin{60^ \circ } \approx 866\left( {\;cm} \right)$.

Câu 21. Một máy nước nóng sử dụng năng lượng mặt trời như ở Hình 20 có các ống hấp nhiệt chân không dài $1,8m$ được đặt trên sân thượng của một toà nhà. Khi tia nắng mặt trời chiếu vuông góc với sân thượng, bóng nắng của các ống hấp nhiệt chân không trên mặt sân dài $1,2\;m$. Các ống hấp nhiệt chân không đó tạo với mặt sân thượng một góc bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Lời giải

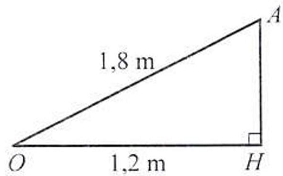
Vẽ $OA$ biểu diễn cho ống hấp nhiệt chân không, $OH$ biểu diễn bóng nắng (hình chiếu vuông góc do tia nắng chiếu vuông góc với mặt sân) của ống đó trên mặt sân. Như vậy góc giữa ống hấp nhiệt chân không với mặt sân bằng $\widehat {AOH}$. Ta có:

$cos\widehat {AOH} = \frac{{OH}}{{OA}} = \frac{{1,2}}{{1,8}} = \frac{2}{3} \Rightarrow \widehat {AOH} \approx {48^ \circ }$.

Vậy góc giữa ống hấp nhiệt chân không với mặt sân thượng bằng khoảng ${48^ \circ }$.