20 Câu Trắc Nghiệm Bài Hai Đường Thẳng Vuông Góc Mức Vận Dụng Giải Chi Tiết

20 câu trắc nghiệm bài hai đường thẳng vuông góc mức vận dụng giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.
Câu 1: Cho tứ diện $ABCD$ có $AB = CD = 2a$. Gọi $M,N$ lần lượt là trung điểm của $AD$ và $BC$. Biết $MN = \sqrt 3 a$, góc giữa hai đường thẳng $AB$ và $CD$ bằng

A. ${45^ \circ }$.

B. ${90^ \circ }$.

C. ${60^ \circ }$.

D. ${30^ \circ }$.

Lời giải

Chọn C

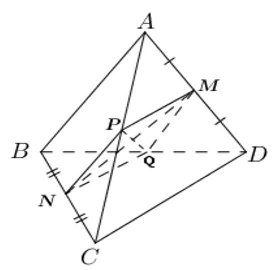
Gọi $P,Q$ lần lượt là trung điểm của $AC$ và $BD$. Khi đó ta có

$\left\{ {\begin{array}{*{20}{l}}
{PM//NQ//CD} \\
{PM = NQ = \frac{{CD}}{2}}
\end{array}} \right.$$ \Rightarrow PMQN$ là hình bình hành

Ta cũng có $MQ//NP//AB,MQ = NP = \frac{{AB}}{2}$.

Do $AB = CD = 2a \Rightarrow PM = MQ = QN = NP = a$.

Gọi $\widehat {\left( {AB,CD} \right)} = \alpha \Rightarrow {\text{cos}}\alpha = \left| {{\text{cos}}\left( {\widehat {MPN}} \right)} \right|$.

Áp dụng định lí Côsin ta có

$M{N^2} = P{M^2} + P{N^2} – 2PM \cdot PN \cdot {\text{cos}}\left( {\widehat {MPN}} \right)$

$ \Leftrightarrow 3{a^2} = {a^2} + {a^2} – 2 \cdot a \cdot a \cdot {\text{cos}}\left( {\widehat {MPN}} \right)$

$ \Leftrightarrow {\text{cos}}\left( {\widehat {MPN}} \right) = \frac{{{a^2} + {a^2} – 3{a^2}}}{{2 \cdot a \cdot a}} = \frac{{ – 1}}{2}$

nên ${\text{cos}}\alpha = \left| {{\text{cos}}\left( {\widehat {MPN}} \right)} \right| = \frac{1}{2} \Rightarrow \widehat {\left( {AB,CD} \right)} = {60^ \circ }$

Câu 2: Cho hình lăng trụ tam giác $ABC \cdot A’B’C’$ có đáy là tam giác đều, các mặt bên là hình chữ nhật; $AB = a$ và $AA’ = a\sqrt 2 $. Góc giữa hai đường thẳng $AB’$ và $BC’$ bằng

A. ${90^ \circ }$.

B. ${30^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Lời giải

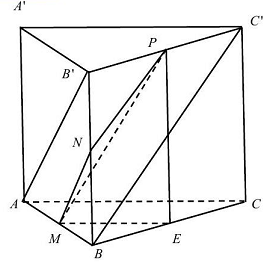
Chọn C

Gọi $M,N,P,E$ lần lượt là trung điểm các đoạn thẳng $AB,BB’,B’C’,BC$.

Suy ra $MN//AB’$ và $NP//BC’$. Khi đó góc giữa đường thẳng $AB’$ và $BC’$ là góc giữa hai đường thẳng $MN$ và $NP$.

Ta có: $MN = NP = \frac{{a\sqrt 3 }}{2}$.

Xét tam giác $PEM$ vuông tại $E,M{P^2} = P{E^2} + M{E^2} = 2{a^2} + \frac{{{a^2}}}{4} = \frac{{9{a^2}}}{4}$.

Áp dụng định lí cosin trong tam giác $MNP$, ta có

${\text{cos}}MNP = \frac{{M{N^2} + N{P^2} – M{P^2}}}{{2 \cdot MN \cdot NP}} = \frac{{\frac{{3{a^2}}}{4} + \frac{{3{a^2}}}{4} – \frac{{9{a^2}}}{4}}}{{2 \cdot \frac{{3{a^2}}}{4}}} = – \frac{1}{2}$.

Do đó góc $MNP$ bằng ${120^ \circ }$ nên góc giữa đường thẳng $AB’$ và $BC’$ bằng ${60^ \circ }$.

Câu 3: Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau và $OA = OB = OC$. Gọi $M$ là trung điểm của $BC$ ( tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng $OM$ và $AB$ bằng

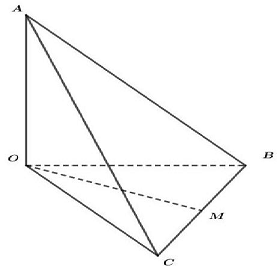
A. ${90^ \circ }$.

B. ${30^ \circ }$.

C. ${60^ \circ }$.

D. ${45^0}$

Lời giải

Chọn C

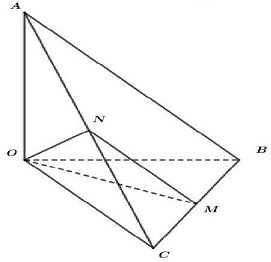
Đặt $OA = a$ suy ra $OB = OC = a$ và $AB = BC = AC = a\sqrt 2 $

Gọi $N$ là trung điểm $AC$ ta có $MN//AB$ và $MN = \frac{{a\sqrt 2 }}{2}$

Suy ra góc $\widehat {\left( {OM,AB} \right)} = \overline {\left( {OM,MN} \right)} $. Xét $\widehat {OMN}$

Trong tam giác $OMN$ có $ON = OM = MN = \frac{{a\sqrt 2 }}{2}$ nên $OMN$ là tam giác đều

Suy ra $\widehat {OMN} = {60^ \circ }$. Vậy $\widehat {\left( {OM,AB} \right)} = \widehat {\left( {OM,MN} \right)} = {60^ \circ }$.

Câu 4: Cho hình lập phương $ABCD \cdot A’B’C’D’$; gọi $M$ là trung điểm của $B’C’$. Góc giữa hai đường thẳng $AM$ và $BC’$ bằng

A. ${45^ \circ }$.

B. ${90^ \circ }$.

C. ${30^ \circ }$.

D. ${60^ \circ }$.

Lời giải

Chọn A

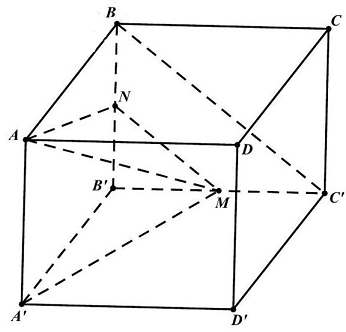
Giả sử cạnh của hình lập phương là $a > 0$.

Gọi $N$ là trung điểm đoạn thẳng $BB’$. Khi đó, $MN//BC’$ nên $\left( {AM,BC’} \right) = \left( {AM,MN} \right)$.

Xét tam giác $A’B’M$ vuông tại $B’$ ta có: $A’M = \sqrt {A'{B^{{\text{‘}}2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}$.

Xét tam giác $AA’M$ vuông tại $A’$ ta có: $AM = \sqrt {A{A^{{\text{‘}}2}} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}$.

Có $AN = A’M = \frac{{a\sqrt 5 }}{2};MN = \frac{{BC’}}{2} = \frac{{a\sqrt 2 }}{2}$.

Trong tam giác $AMN$ ta có:

${\text{cos}}\widehat {AMN} = \frac{{M{A^2} + M{N^2} – A{N^2}}}{{2 \cdot MA \cdot MN}}$

$ = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} – \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{{6{a^2}}}{4} \cdot \frac{4}{{6{a^2}\sqrt 2 }} = \frac{1}{{\sqrt 2 }}$.

Suy ra $\widehat {AMN} = {45^ \circ }$.

Vậy $\left( {AM,BC’} \right) = \left( {AM,MN} \right) = \widehat {AMN} = {45^ \circ }$.

Câu 5: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Gọi $M$ là trung điểm của $DD’$ (Tham khảo hình vẽ). Tính cô-sin của góc giữa hai đường thẳng $B’C$ và $C’M$

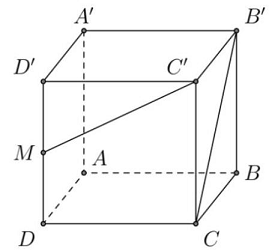
A. $\frac{1}{{\sqrt {10} }}$.

B. $\frac{1}{3}$.

C. $\frac{1}{{\sqrt 3 }}$.

D. $\frac{{2\sqrt 2 }}{9}$.

Lời giải

Chọn A

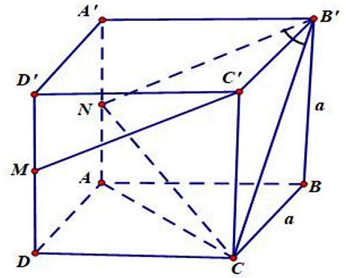
Gọi $N$ là trung điểm của $AA’ \Rightarrow B’N//C’M \Rightarrow \overline {\left( {B’C,C’M} \right)} = \overline {\left( {B’C,B’N} \right)} $

Xét tam giác $B’NC$ có $B’N = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2};B’C = a\sqrt 2 ;NC = \sqrt {2{a^2} + \frac{{{a^2}}}{4}} = \frac{{3a}}{2}$

Vậy ${\text{cos}}\widehat {\left( {B’C,C’M} \right)} = \left| {{\text{cos}}\widehat {NB’C}} \right|$

$ = \frac{{\left| {B'{N^2} + B'{C^2} – N{C^2}} \right|}}{{2B’N \cdot B’C}} = \frac{{{a^2}}}{{2 \cdot \frac{{a\sqrt 5 }}{2} \cdot a\sqrt 2 }} = \frac{1}{{\sqrt {10} }}$

Câu 6: Cho tứ diện $ABCD$. Gọi $P,Q$ lần lượt là trung điểm của các cạnh $BC,AD$. Giả sử $AB = CD = a$ và $PQ = \frac{{a\sqrt 3 }}{2}$. Số đo góc giữa hai đường thẳng $AB$ và $CD$ là

A. ${90^ \circ }$.

B. ${45^ \circ }$.

C. 30 .

D. ${60^ \circ }$.

Lời giải

Chọn D

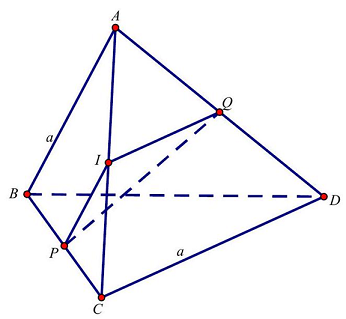
Gọi $I$ là trung điểm của $AC$, khi đó $\left\{ {\begin{array}{*{20}{l}}
{IP//AB} \\
{IQ//CD}
\end{array}} \right.$ do $IP,IQ$ lần lượt là các đường trung bình của tam giác $CAB$ và $ACD$.

Suy ra góc giữa hai đường thẳng $AB$ và $CD$ là góc giữa hai đường thẳng $IP$ và $IQ$.

Xét tam giác $IPQ$, ta có

${\text{cos}}\widehat {PIQ} = \frac{{I{P^2} + I{Q^2} – P{Q^2}}}{{2IP \cdot IQ}} = \frac{{{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{a}{2}} \right)}^2} – {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2.{{\left( {\frac{a}{2}} \right)}^2}}} = – \frac{1}{2}$

suy ra $\widehat {PIQ} = {120^ \circ }$.

Vậy góc giữa hai đường thẳng $AB$ và $CD$ có số đo là ${180^ \circ } – {120^ \circ } = {60^ \circ }$.

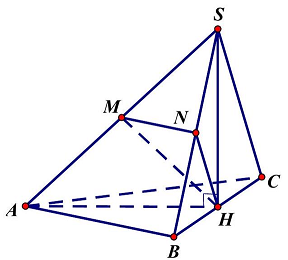
Câu 7: Cho hình chóp $S.ABC$ có $SA = SB = SC = AB = AC = a,BC = a\sqrt 2 $. Tính số đo của góc giữa hai đường thẳng $AB$ và $SC$ ta được kết quả:

A. ${90^ \circ }$.

B. ${30^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Lời giải

Gọi $H$ là hình chiếu vuông góc của $S$ lên mặt phẳng $\left( {ABC} \right)$, theo đầu bài $SA = SB = SC$ và tam giác $\vartriangle ABC$ vuông cân tại $A$ ta có $H$ là trung điểm của $BC$. Gọi $M,N$ lần lượt là trung điểm của $SA,SB$ ta có: $\left\{ {\begin{array}{*{20}{l}}
{MN//AB} \\
{HN//SC}
\end{array} \Rightarrow } \right.$ Góc giữa $AB$ và $SC$ là góc giữa $MN$ và $HN$.

Xét tam giác $\vartriangle MNH$ ta có: $MN = \frac{{AB}}{2} = \frac{a}{2};HN = \frac{{SC}}{2} = \frac{a}{2};MH = \frac{{SA}}{2} = \frac{a}{2}$ ( Do $\vartriangle SHA$ vuông tại $H)$

$ \Rightarrow $ tam giác $\vartriangle MNH$ là tam giác đều $ \Rightarrow \widehat {MNH} = {60^ \circ }$. Vậy góc cần tìm là ${60^ \circ }$.

Câu 8: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Gọi $M$ trung điểm các cạnh $CD$. cosin của góc giữa $AC$ và $C’M$ là

A. 0 .

B. $\frac{{\sqrt 2 }}{2}$.

C. $\frac{1}{2}$.

D. $\frac{{\sqrt {10} }}{{10}}$.

Lời giải

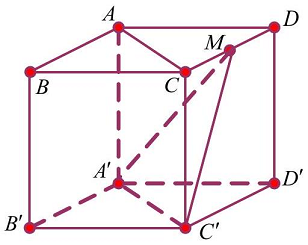
Ta có $AC//A’C’$ nên góc giữa $AC$ và $C’M$ cũng bằng góc giữa $A’C’$ và $C’M$ là $\widehat {A’C’M}$.

Gọi cạnh của hình lập phương có độ dài là $a$. Khi đó $A’C’ = a\sqrt 2 ,C’M = \frac{{a\sqrt 5 }}{2}$ ( trong tam gics vuông $CC’M$ có $CM = \frac{a}{2}$ ), $A’M = \frac{{3a}}{2}$ ( trong tam giác vuông $A’MD,MD = \frac{a}{2},A’D = a\sqrt 2 $ ).

Xét tam giác $A’MC’$ ta có ${\text{cos}}\widehat {A’C’M} = \frac{{{{\left( {A’C’} \right)}^2} + C'{M^2} – A'{M^2}}}{{2A’M \cdot C’M}} = \frac{1}{2}$.

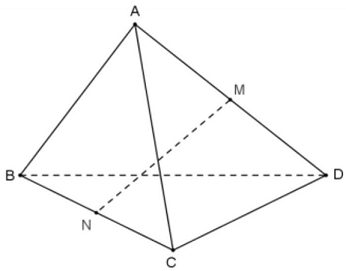
Câu 9: Cho tứ diện $ABCD$ có $AB = CD = a$. Gọi $M$ và $N$ lần lượt là trung điểm của $AD$ và $BC$. Xác định độ dài đoạn thẳng $MN$ để góc giữa hai đường thẳng $AB$ và $MN$ bằng ${30^ \circ }$.

A. $MN = \frac{a}{2}$.

B. $MN = \frac{{a\sqrt 3 }}{2}$.

C. $MN = \frac{{a\sqrt 3 }}{3}$.

D. $MN = \frac{a}{4}$.

Lời giải

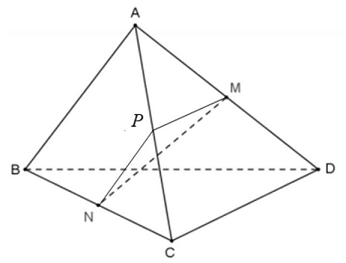
Gọi $P$ là trung điểm của $AC$. Suy ra $PM = \frac{1}{2}CD = \frac{1}{2}AB = PN$.

Do đó tam giác $PMN$ cân tại $P$.

Lại có góc giữa $AB$ và $MN$ bằng ${30^ \circ }$ nên góc giữa $MN$ và $PN$ bằng ${30^ \circ }$.

Vậy tam giác $PMN$ là tam giác cân có góc ở đỉnh bằng ${120^ \circ }$.

Ta có $PN \cdot \sqrt 3 = MN$ nên $MN = \frac{{a\sqrt 3 }}{2}$.

Câu 10: Cho tứ diện $ABCD$ có $AC = 3a,BD = 4a$. Gọi $M,N$ lần lượt là trung điểm $AD$ và $BC$. Biết $AC$ vuông góc $BD$. Tính $MN$.

A. $MN = \frac{{5a}}{2}$.

B. $MN = \frac{{7a}}{2}$.

C. $MN = \frac{{a\sqrt 7 }}{2}$.

D. $MN = \frac{{a\sqrt 5 }}{2}$.

Lời giải

Chọn A

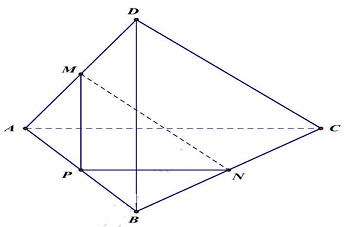
Gọi $P$ là trung điểm $AB$

Ta có $\left\{ {\begin{array}{*{20}{l}}
{AC//PN} \\
{BD//PM}
\end{array} \Rightarrow PN \bot PM} \right.$ và $PN = \frac{{AC}}{2} = \frac{{3a}}{2};PM = \frac{{BD}}{2} = 2a$

$MN = \sqrt {P{M^2} + P{N^2}} = \frac{{5a}}{2}$

Câu 11: Cho hình lăng trụ $ABCD \cdot A’B’C’D’$ có đáy là hình chữ nhật và $\widehat {CAD} = {40^ \circ }$. Số đo góc giữa hai đường thẳng $AC,B’D’$ là

A. ${40^ \circ }$

B. ${20^ \circ }$.

C. ${50^ \circ }$.

D. ${80^ \circ }$.

Lời giải

Chọn D

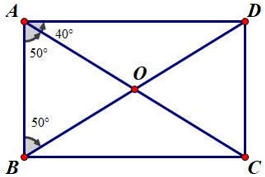
Vì $BD//B’D’$ nên $\widehat {\left( {AC;B’D’} \right)} = \widehat {\left( {AC;BD} \right)} = \widehat {AOB} = {80^ \circ }$ với ${\text{O}}$ là tâm hình chữ nhật $ABCD$.

Câu 12: Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng $a$. Góc giữa hai đường thẳng $CD’$ và $A’C’$ bằng.

A. ${30^ \circ }$.

B. ${90^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Lời giải

Chọn C

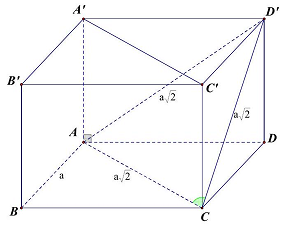
Ta thấy $A’C’//AC \Rightarrow \overline {\left( {CD’,A’C’} \right)} = \overline {\left( {CD’,AC} \right)} = \varphi $

Do các mặt của hình lập phương bằng nhau nên các đướng chéo $AC = CD’ = AD’ = a\sqrt 2 $

Suy ra $\vartriangle ACD’$ đều nên $\overline {\left( {CD’,A’C’} \right)} = \overline {\left( {CD’,AC} \right)} = \varphi = {60^ \circ }$.

Câu 13: Cho tứ diện $ABCD$ có $AB = AC = AD = 1;\widehat {BAC} = {60^ \circ };\widehat {BAD} = {90^ \circ };\widehat {DAC} = {120^ \circ }$. Tính côsin của góc tạo bởi hai đường thẳng $AG$ và $CD$, trong đó $G$ là trọng tâm tam giác $BCD$.

A. $\frac{1}{{\sqrt 6 }}$.

B. $\frac{1}{3}$.

C. $\frac{1}{6}$.

D. $\frac{1}{{\sqrt 3 }}$.

Lời giải

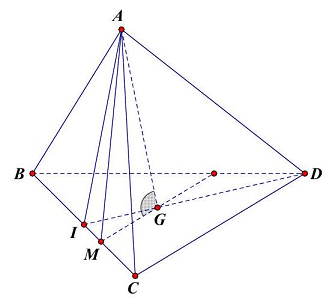
$\vartriangle ABC$ đều $ \Rightarrow BC = 1$.

$\vartriangle ACD$ cân tại $A$ có $CD = \sqrt {A{C^2} + A{D^2} – 2AC \cdot AD \cdot {\text{cos}}{{120}^ \circ }} = \sqrt 3 $.

$\vartriangle ABD$ vuông cân tại $A$ có $BD = \sqrt 2 $.

$\vartriangle BCD$ có $C{D^2} = B{C^2} + B{D^2} \Rightarrow \vartriangle BCD$ vuông tại $B$.

Dựng đường thẳng $d$ qua $G$ và song song $CD$, cắt $BC$ tại $M$.

Ta có $MG//CD \Rightarrow \left( {AG,CD} \right) = \left( {AG,MG} \right)$.

Gọi $I$ là trung điểm của $BC$, xét $\vartriangle BDI$ vuông tại $B$ có $DI = \sqrt {B{D^2} + B{I^2}} = \sqrt {2 + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{3}{2}$.

Ta có $\frac{{IM}}{{IC}} = \frac{{MG}}{{CD}} = \frac{{IG}}{{ID}} = \frac{1}{3} \Rightarrow IM = \frac{1}{3} \cdot IC$

$ = \frac{1}{3} \cdot \frac{{BC}}{2} = \frac{1}{6};MG = \frac{1}{3}.CD = \frac{{\sqrt 3 }}{3};IG = \frac{1}{3} \cdot ID = \frac{1}{2}$.

Xét $\vartriangle AIM$ vuông tại $I$ có $AM = \sqrt {A{I^2} + I{M^2}} = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{1}{6}} \right)}^2}} = \frac{{\sqrt 7 }}{3}$.

${\text{cos}}\widehat {AID} = \frac{{A{I^2} + I{D^2} – A{D^2}}}{{2AI \cdot ID}} = \frac{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{3}{2}} \right)}^2} – {1^2}}}{{2 \cdot \frac{{\sqrt 3 }}{2} \cdot \frac{3}{2}}} = \frac{{4\sqrt 3 }}{9}$

$AG = \sqrt {A{I^2} + I{G^2} – 2AI \cdot IG \cdot {\text{cos}}\widehat {AID}} $

$ = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2} – 2 \cdot \frac{{\sqrt 3 }}{2} \cdot \frac{1}{2} \cdot \frac{{4\sqrt 3 }}{9}} = \frac{{\sqrt 3 }}{3}$.

Xét $\vartriangle AMG$ có

${\text{cos}}\left( {AG,MG} \right) = \left| {{\text{cos}}\widehat {AGM}} \right|$

$ = \left| {\frac{{A{G^2} + G{M^2} – A{M^2}}}{{2 \cdot AG \cdot GM}}} \right| = \left| {\frac{{{{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2} – {{\left( {\frac{{\sqrt 7 }}{3}} \right)}^2}}}{{2 \cdot \frac{{\sqrt 3 }}{3} \cdot \frac{{\sqrt 3 }}{3}}}} \right| = \frac{1}{6}$

Câu 14: Cho hình vuông $ABCD$ cạnh $4a$, lấy $H,K$ lần lượt trên các cạnh $AB,AD$ sao cho $BH = 3HA,AK = 3KD$. Trên đường thẳng vuông góc với mặt phẳng $\left( {ABCD} \right)$ tại $H$ lấy điểm $S$ sao cho $\widehat {SBH} = {30^ \circ }$. Gọi $E$ là giao điểm của $CH$ và $BK$. Tính cosin của góc giữa hai đường thẳng $SE$ và $BC$.

A. $\frac{{28}}{{5\sqrt {39} }}$.

B. $\frac{{18}}{{5\sqrt {39} }}$.

C. $\frac{{36}}{{5\sqrt {39} }}$.

D. $\frac{9}{{5\sqrt {39} }}$.

Lời giải

Gọi $I$ là hình chiếu vuông góc của $E$ lên $AB$ ta có $\vartriangle ABD = \vartriangle BCH$.

$ \Rightarrow \widehat {ABD} = \widehat {BCH} \Rightarrow \widehat {HEB} = {90^ \circ }$.

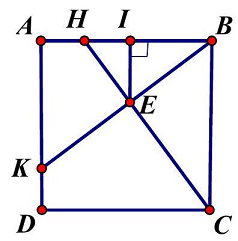
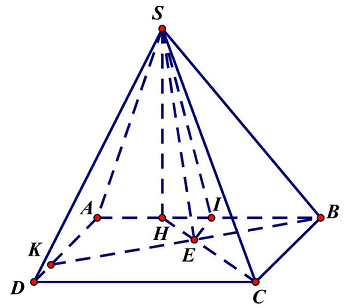
Ta có: ${\text{cos}}\left( {SE;BC} \right) = {\text{cos}}\left( {SE;EI} \right) = \left| {{\text{cos}}\widehat {SEI}} \right|,SH = BH \cdot {\text{tan}}{30^ \circ } = a\sqrt 3 $.

$\frac{{HB}}{{HC}} = \frac{{HE}}{{HB}} \Rightarrow HE = \frac{{H{B^2}}}{{HC}} = \frac{{9a}}{5},$

$SE = \sqrt {S{H^2} + H{E^2}} = \sqrt {3{a^2} + \frac{{81{a^2}}}{{25}}} = \frac{{2a\sqrt {39} }}{5}$.

$\frac{{HE}}{{HB}} = \frac{{HI}}{{HE}} \Rightarrow HI = \frac{{H{E^2}}}{{HB}} = \frac{{27a}}{{25}},$

$SI = \sqrt {S{H^2} + H{I^2}} = \sqrt {3{a^2} + {{\left( {\frac{{27a}}{{25}}} \right)}^2}} = \frac{{2a\sqrt {651} }}{{25}}$

$\frac{{EI}}{{BC}} = \frac{{HI}}{{HB}} = \frac{9}{{25}} \Rightarrow EI = \frac{{36a}}{{25}}$

Áp dụng định lý cosin cho tam giác $SEI$ ta được:

${\text{cos}}\widehat {SEI} = \frac{{S{E^2} + E{I^2} – S{I^2}}}{{2 \cdot SE \cdot EI}}$

$ = \frac{{{{\left( {\frac{{2a\sqrt {39} }}{5}} \right)}^2} + {{\left( {\frac{{36a}}{{25}}} \right)}^2} – {{\left( {\frac{{2a\sqrt {651} }}{{25}}} \right)}^2}}}{{2 \cdot \frac{{2a\sqrt {39} }}{5} \cdot \frac{{36a}}{{25}}}} = \frac{{18a}}{{5\sqrt {39} }}$

Câu 15: Cho hình lập phương $ABCD \cdot A’B’C’D’$. Gọi $M,N,P$ lần lượt là trung điểm các cạnh $AB$, $BC,C’D’$. Xác định góc giữa hai đường thẳng $MN$ và $AP$.

A. ${60^ \circ }$.

B. ${90^ \circ }$

C. ${30^ \circ }$.

D. ${45^ \circ }$.

Lời giải

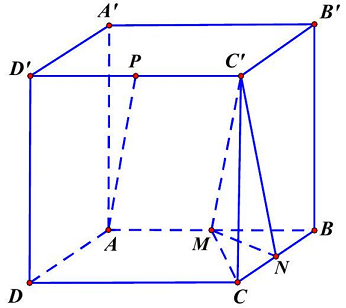
Ta có tứ giác $AMC’P$ là hình bình hành nên $AP//MC’ \Rightarrow \left( {\widehat {MN,AP}} \right) = \left( {\widehat {MN,MC’}} \right) = \widehat {NMC’}$.

Gọi cạnh hình vuông có độ dài bằng $a$.

Xét tam giác $C’CM$ vuông tại $C$ có $C’M = \sqrt {C'{C^2} + M{C^2}} = \sqrt {C'{C^2} + B{C^2} + M{B^2}} = \frac{{3a}}{2}$.

Xét tam giác $C’CN$ vuông tại $C$ có $C’N = \sqrt {C'{C^2} + C{N^2}} = \frac{{\sqrt 5 a}}{2}$.

Mà $MN = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}$.

Xét tam giác $C’CM$ có ${\text{cos}}\widehat {NMC’} = \frac{{M{C^{{\text{‘}}2}} + M{N^2} – C'{N^2}}}{{2MC’ \cdot MN}} = \frac{{\sqrt 2 }}{2}$

$ \Rightarrow \widehat {NMC’} = {45^ \circ } \Rightarrow \left( {\widehat {MN,AP}} \right) = {45^ \circ }$.

Câu 16: Cho tứ diện $ABCD$ có tất cả các cạnh đều bằng nhau, $M$là trung điểm của cạnh $BC$. Tính giá trị của ${\text{cos}}\left( {AB,DM} \right)$.

A. $\frac{{\sqrt 3 }}{2}$.

B. $\frac{{\sqrt 3 }}{6}$.

C. $\frac{1}{2}$.

D. $\frac{{\sqrt 2 }}{2}$.

Lời giải

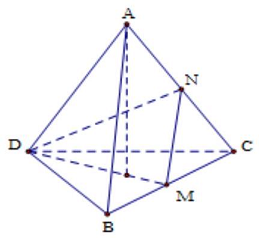
Giả sử cạnh của tứ diện đều bằng $a$.

Gọi $N$ là trung điểm của $AC$.

Khi đó: $\left( {\overline {AB,DM} } \right) = \left( {\overline {MN,DM} } \right)$

Ta có: $MN = \frac{a}{2},DM = DN = \frac{{a\sqrt 3 }}{2}$.

${\text{cos}}\widehat {NM{\text{D}}} = \frac{{M{N^2} + M{{\text{D}}^2} – N{{\text{D}}^2}}}{{2 \cdot MN \cdot M{\text{D}}}} = \frac{{\frac{{{a^2}}}{4}}}{{2 \cdot \frac{a}{2} \cdot \frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{6}$

Vậy ${\text{cos}}\left( {AB,DM} \right) = \frac{{\sqrt 3 }}{6}$.

Câu 17: Cho tứ diện $S.ABC$ có $SA = SB = SC = AB = AC = a;BC = a\sqrt 2 $. Góc giữa hai đường thẳng $AB$ và $SC$ bằng

A. ${0^ \circ }$.

B. ${120^ \circ }$.

C. ${60^ \circ }$.

D. ${90^ \circ }$.

Lời giải

Chọn C

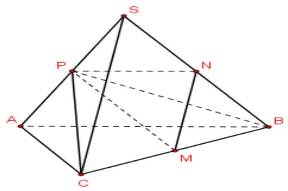
Gọi $M,N,P$ lần lượt là trung điểm của $BC,SB,SA$.

Góc giữa $AB$ và $SC$ là góc giữa $PN$ và $MN$.

$MN = \frac{a}{2} = NP$

$PC = BP = \frac{{a\sqrt 3 }}{2} \Rightarrow PM = \sqrt {P{C^2} – C{M^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} – {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{a}{2}$

Suy ra tam giác $MNP$ là tam giác đều $ \Rightarrow \widehat {MNP} = {60^ \circ }$.

Vậy góc giữa $AB$ và $SC$ bằng ${60^ \circ }$.

Câu 18: Cho tứ diện $ABCD$ có $AB,AC,AD$ đôi một vuông góc với nhau, biết $AB = AC = AD = 1$. Số đo góc giữa hai đường thẳng $AB$ và $CD$ bằng

A. ${45^ \circ }$.

B. ${60^ \circ }$.

C. ${30^ \circ }$.

D. ${90^ \circ }$.

Lời giải

Chọn D

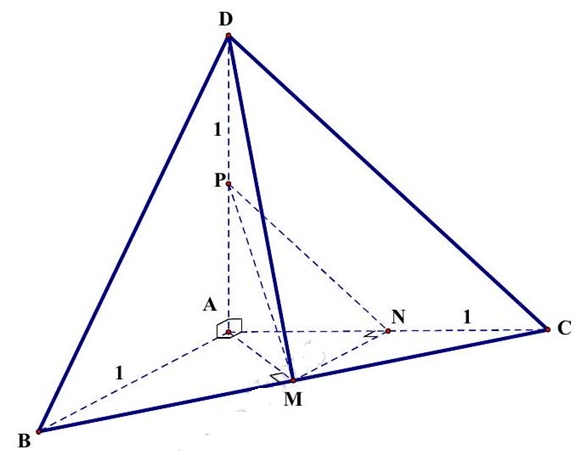
Gọi $M,N,P$ lần lượt là trung điểm của các cạnh $BC,AC,AD$.

Trong $\vartriangle ABC$, có $\left\{ {\begin{array}{*{20}{l}}
{MN//AB} \\
{MN = \frac{1}{2}AB = \frac{1}{2}}
\end{array}} \right.$ (Tính chất đường trung bình)

Trong $\vartriangle ACD$, có $\left\{ {\begin{array}{*{20}{l}}
{NP//CD} \\
{NP = \frac{1}{2}CD = \frac{{\sqrt 2 }}{2}}
\end{array}} \right.$ (Tính chất đường trung bình)

Trong $\vartriangle AMP$, có $MP = \sqrt {A{P^2} + A{M^2}} = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{MN//AB} \\
{NP//CD}
\end{array} \Rightarrow \left( {AB;CD} \right) = \left( {MN;NP} \right) = \widehat {MNP}} \right.$

Áp dụng định lý Cosin cho $\vartriangle MNP$, có

${\text{cos}}\widehat {MNP} = \frac{{N{P^2} + N{M^2} – M{P^2}}}{{2NP \cdot NM}} = \frac{{{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2} – {{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{{2 \cdot \frac{{\sqrt 2 }}{2} \cdot \frac{1}{2}}} = 0 \Rightarrow \widehat {MNP} = {90^ \circ }$

Hay $\left( {AB;CD} \right) = {90^ \circ }$.

Câu 19: Cho tứ diện $ABCD$ có $AB = CD = 2a$. Gọi $M,N$ lần lượt là trung điểm $AD$ và $BC$. Biết $MN = a\sqrt 3 $, góc giữa hai đường thẳng $AB$ và $CD$ bằng.

A. ${45^0}$.

B. ${90^ \circ }$.

C. ${60^ \circ }$.

D. ${30^ \circ }$.

Lời giải

Chọn C

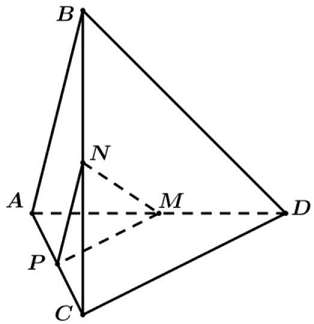
Gọi $P$ là trung điểm $AC$, ta có $PM//CD$ và $PN//AB$, suy ra $\left( {\widehat {AB,CD}} \right) = \left( {\widehat {PM,PN}} \right)$.

Dễ thấy $PM = PN = a$.

Xét $\vartriangle PMN$ ta có ${\text{cos}}\widehat {MPN} = \frac{{P{M^2} + P{N^2} – M{N^2}}}{{2PM \cdot PN}} = \frac{{{a^2} + {a^2} – 3{a^2}}}{{2 \cdot a \cdot a}} = – \frac{1}{2}$

$ \Rightarrow \widehat {MPN} = {120^ \circ } \Rightarrow \left( {\widehat {AB,CD}} \right) = {180^ \circ } – {120^ \circ } = {60^ \circ }$.