Các Dạng Toán Trắc Nghiệm Bài Khoảng Cách Lớp 11 Giải Chi Tiết

Các dạng toán trắc nghiệm bài Khoảng cách lớp 11 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Dạng 1. Tính khoảng cách liên quan đến hình chóp

Câu 1: Cho hình chóp $S.ABC$ có đáy là tam giác vuông đỉnh $B,AB = SA = a$, $SA$ vuông góc với mặt phẳng đáy. Khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng

A. $\frac{a}{2}$.

B. $a$.

C. $\frac{{a\sqrt 6 }}{3}$.

D. $\frac{{a\sqrt 2 }}{2}$.

Lời giải

Chọn D

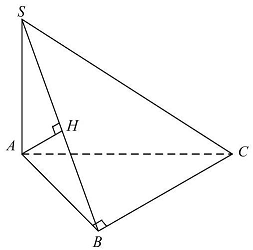
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{AB \bot BC} \\
{SA \bot BC}
\end{array} \Rightarrow \left( {SAB} \right) \bot BC} \right.$

$ \Rightarrow \left( {SAB} \right) \bot (SBC)$ (1)

Kẻ $AH \bot SB$ (2)

Từ (1) và (2) $ \Rightarrow AH \bot \left( {SBC} \right)$

$ \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH = \frac{1}{2}SB = \frac{{a\sqrt 2 }}{2}$

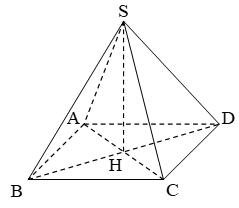
Câu 2: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy là $a\sqrt 2 $ và tam giác $SAC$ đều. Tính khoảng cách từ đỉnh $S$ đến đáy $ABCD$ của hình chóp.

A. $2a$.

B. $a\sqrt 2 $.

C. $a\sqrt 3 $.

D. $a$.

Lời giải

Chọn C

Gọi $H$ là tâm của đáy $ABCD$.

Ta có: $SH \bot (ABCD)$ (Do $S.ABCD$ là hình chóp đều)

$ \Rightarrow d(S;(ABCD)) = SH$

Hình chóp tứ giác đều $S.ABCD$ nên $ABCD$ là hình vuông có cạnh bằng $a\sqrt 2 $

Suy ra $AC = a\sqrt 2 .\sqrt 2 = 2a$.

$SH = \frac{{AC\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 $ (Do $SH$ là đường cao tam giác đều)

Vậy $d(S;(ABCD)) = SH = a\sqrt 3 $

Câu 3: Cho hình chóp $SABC$ có đáy là tam giác vuông tại $A,AB = a,AC = a\sqrt 3 ,SA$ vuông góc với mặt phẳng đáy và $SA = 2a$. Khoảng cách từ điểm $A$ dến mặt phẳng $\left( {SBC} \right)$ bằng

A. $\frac{{a\sqrt {57} }}{{19}}$.

B. $\frac{{2a\sqrt {57} }}{{19}}$.

C. $\frac{{2a\sqrt 3 }}{{19}}$.

D. $\frac{{2a\sqrt {38} }}{{19}}$.

Lời giải

Chọn B

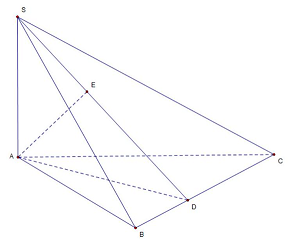
Từ $A$ kẻ $AD \bot BC$ mà $SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC$

$ \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow \left( {SAD} \right) \bot \left( {SBC} \right)$ mà $\left( {SAD} \right) \cap \left( {SBC} \right) = SD$

$ \Rightarrow $ Từ $A$ kẻ $AE \bot SD \Rightarrow AE \bot \left( {SBC} \right)$

$ \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AE$

Trong $\vartriangle ABC$ vuông tại $A$ ta có: $\frac{1}{{A{D^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{3{a^2}}}$

Trong $\vartriangle SAD$ vuông tại $A$ ta có: $\frac{1}{{A{E^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{D^2}}} = \frac{{19}}{{12{a^2}}} \Rightarrow AE = \frac{{2a\sqrt {57} }}{{19}}$

Câu 4: Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$, góc giữa hai mặt phẳng $\left( {ABC} \right)$ và $\left( {SBC} \right)$ là ${60^ \circ }$. Khoảng cách từ $A$ đến mặt phẳng $\left( {ABC} \right)$ bằng

A. $\frac{{3a}}{2}$.

B. $\frac{a}{2}$.

C. $a\sqrt 3 $.

D. $\frac{a}{{\sqrt 3 }}$.

Lời giải

Chọn A

Ta có: $SA \bot \left( {ABC} \right)$

$ \Rightarrow d(S;(ABC)) = SA$

Gọi $I$ là trung điểm $BC$, khi đó $BC \bot AI$

Mặt khác $BC \bot AI,BC \bot SA \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot SI$

Suy ra góc giữa hai mặt phẳng $\left( {ABC} \right)$ và $\left( {SBC} \right)$ là $\widehat {SIA}$.

Tam giác $SIA$ vuông tại $A$ nên $tan\widehat {SIA} = \frac{{SA}}{{AI}} \Leftrightarrow SA = IA \cdot tan\widehat {SIA} = \frac{{a\sqrt 3 }}{2} \cdot \sqrt 3 = \frac{{3a}}{2}$.

Câu 5: Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B,2SA = AC = 2a$ và $SA$ vuông góc với đáy. Khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ là

A. $\frac{{2a\sqrt 6 }}{3}$.

B. $\frac{{4a\sqrt 3 }}{3}$.

C. $\frac{{a\sqrt 6 }}{3}$.

D. $\frac{{a\sqrt 3 }}{3}$.

Lời giải

Chọn C

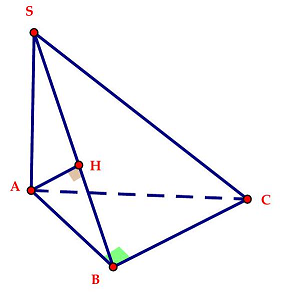
Kẻ $AH \bot SB\left( {H \in SB} \right)$.

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA\left( {SA \bot \left( {ABC} \right)} \right)}
\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH \subset \left( {SAB} \right)} \right.$.

Vì $\left\{ {\begin{array}{*{20}{l}}
{AH \bot SB} \\
{AH \bot BC}
\end{array} \Rightarrow AH \bot \left( {SBC} \right)} \right.$.

Do đó khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ là ${d_{\left( {A,SBC} \right))}} = AH$.

Xét tam giác $ABC$ vuông cân tại $B$, có $AC = 2a \Rightarrow AB = \frac{{AC}}{{\sqrt 2 }} = \sqrt 2 a$.

Xét tam giác $SAB$ vuông tại $A$, ta có: $\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{2{a^2}}} = \frac{3}{{2{a^2}}}$

$ \Rightarrow A{H^2} = \frac{{2{a^2}}}{3} \Rightarrow AH = \frac{{\sqrt 6 a}}{3}$.

Vậy khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ là $d\left( {A,\left( {SBC} \right)} \right) = AH = \frac{{\sqrt 6 a}}{3}$.

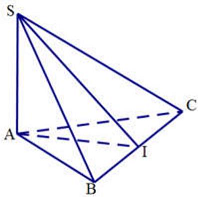
Câu 6: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B$ và cạnh bên $SB$ vuông góc với mặt phẳng đáy. Biết $SB = 3a,AB = 4a,BC = 2a$. Khoảng cách từ $B$ đến mặt phẳng $\left( {SAC} \right)$ bằng

A. $\frac{{12\sqrt {61} a}}{{61}}$.

B. $\frac{{3\sqrt {14} a}}{{14}}$.

C. $\frac{{4a}}{5}$.

D. $\frac{{12\sqrt {29} a}}{{29}}$.

Lời giải

Chọn A

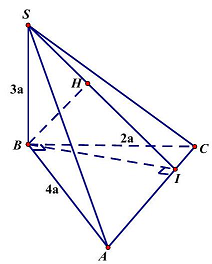
Từ $B$ kẻ $BI \bot AC$ nối $S$ với $I$ và kẻ $BH \bot SI$ dễ thấy $BH$ là khoảng cách từ $B$ đến mặt phẳng $\left( {SAC} \right)$

Ta có $B.SAC$ là tam diện vuông tại $B$ nên:

$\frac{1}{{B{H^2}}} = \frac{1}{{B{S^2}}} + \frac{1}{{B{C^2}}} + \frac{1}{{B{A^2}}}$

$ = \frac{1}{{9{a^2}}} + \frac{1}{{4{a^2}}} + \frac{1}{{16{a^2}}} = \frac{{61}}{{144{a^2}}} \Rightarrow BH = \frac{{12\sqrt {61} a}}{{61}}$

Câu 7: Cho hình chóp $S.ABC$ có đáy là tam giác vuông đỉnh $B,AB = a,SA$ vuông góc với mặt phẳng đáy và $SA = 2a$. Khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng

A. $\frac{{2\sqrt 5 a}}{5}$.

B. $\frac{{\sqrt 5 a}}{3}$.

C. $\frac{{2\sqrt 2 a}}{3}$.

D. $\frac{{\sqrt 5 a}}{5}$.

Lời giải

Chọn A

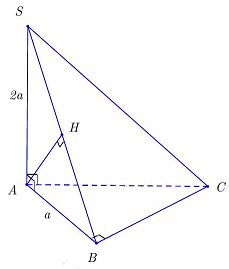
Ta có $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.$.

Kẻ $AH \bot SB$. Khi đó $AH \bot BC \Rightarrow AH \bot \left( {SBC} \right)$

$ \Rightarrow AH$ là khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$.

Ta có $\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{{a^2}}} = \frac{5}{{4{a^2}}} \Rightarrow A{H^2} = \frac{{4{a^2}}}{5} \Rightarrow AH = \frac{{2\sqrt 5 a}}{5}$.

Câu 8: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA \bot \left( {ABCD} \right)$. Gọi $I$ là trung điểm của $SC$. Khoảng cách từ $I$ đến mặt phẳng $\left( {ABCD} \right)$ bẳng độ dài đoạn thẳng nào?

A. $IB$.

B. IC .

C. $IA$.

D. $IO$.

Lời giải

Chọn D

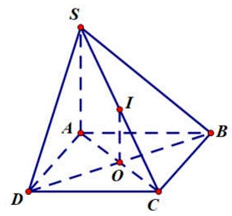
Từ giả thiết suy ra $OI$ là đường trung bình của $\vartriangle SAC$, do đó $OI//SA$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{IO//SA} \\
{SA \bot \left( {ABCD} \right)}
\end{array} \Rightarrow IO \bot \left( {ABCD} \right)} \right.$.

Vậy $d\left( {I,\left( {ABCD} \right)} \right) = OI$.

Câu 9: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $\sqrt 3 a,SA$ vuông góc với mặt phẳng đáy và $SA = a$. Khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng

A. $\frac{{\sqrt 5 a}}{3}$.

B. $\frac{{\sqrt 3 a}}{2}$.

C. $\frac{{\sqrt 6 a}}{6}$.

D. $\frac{{\sqrt 3 a}}{3}$.

Lời giải

Chọn B

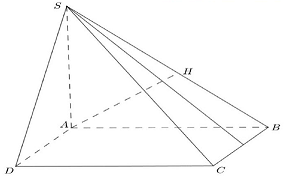
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.$

$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{\left( {SAB} \right) \bot \left( {SBC} \right)} \\
{\left( {SAB} \right) \cap \left( {SBC} \right) = SB}
\end{array}} \right.$

Trong mặt phẳng $\left( {SAB} \right):$Kẻ $AH \bot SB \Rightarrow AH = d\left( {A;\left( {SBC} \right)} \right)$

$\begin{array}{*{20}{r}}
{}&{\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{3{a^2}}} = \frac{4}{{3{a^2}}}.} \\
{}&{\; \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH = \frac{{\sqrt 3 a}}{2}}
\end{array}$

Câu 10: Cho hình chóp $S \cdot ABC$ có đáy là tam giác vuông cân tại $C,BC = a,SA$ vuông góc với mặt phẳng đáy và $SA = a$. Khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng

A. $\sqrt 2 a$.

B. $\frac{{\sqrt 2 a}}{2}$.

C. $\frac{a}{2}$.

D. $\frac{{\sqrt 3 a}}{2}$.

Lời giải

Chọn B

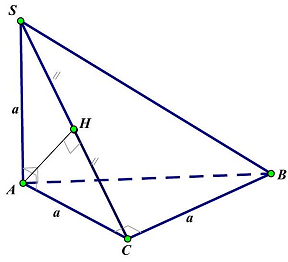
Vì $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AC} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAC} \right)} \right.$

Khi đó $\left( {SBC} \right) \bot \left( {SAC} \right)$ theo giao tuyến là $SC$.

Trong $\left( {SAC} \right)$, kẻ $AH \bot SC$ tại $H$ suy ra $AH \bot \left( {SBC} \right)$ tại $H$.

Khoảng cách từ $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng $AH$.

Ta có $AC = BC = a,SA = a$ nên tam giác $SAC$ vuông cân tại $A$.

Suy ra $AH = \frac{1}{2}SC = \frac{1}{2}a\sqrt 2 $.

Câu 11: Cho hình chóp tứ giác đều $S.ABCD$ có đáy là hình vuông cạnh $a$. Gọi $M$ là trung điểm của $SD$. Khoảng cách từ $M$ đến mặt phẳng $\left( {SAC} \right)$ bằng

A. $\frac{{a\sqrt 2 }}{2}$.

B. $\frac{{a\sqrt 2 }}{4}$.

C. $\frac{a}{2}$.

D. $\frac{a}{4}$.

Lời giải

Chọn B

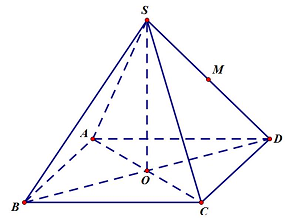
$d\left( {M,\left( {SAC} \right)} \right) = \frac{1}{2}d\left( {D,\left( {SAC} \right)} \right) = \frac{1}{2}DO = \frac{1}{4}BD = \frac{{a\sqrt 2 }}{4}$.

Câu 12: Cho tứ diện đều $S.ABCD$ có tất cả các cạnh đều bằng $2a$, gọi $M$ là điểm thuộc cạnh $AD$ sao cho $DM = 2MA$. Tính khoảng cách từ $M$ đến mặt phẳng $\left( {BCD} \right)$.

A. $\frac{{2a\sqrt 6 }}{9}$.

B. $a\sqrt 6 $.

C. $\frac{{4a\sqrt 6 }}{9}$.

D. $\frac{{2a\sqrt 6 }}{3}$.

Lời giải

Chọn C

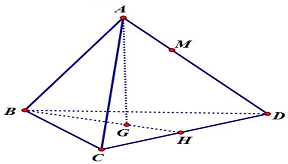
Gọi $H$ là trung điểm $BC,G$ là trọng tâm tam giác $BCD,AG$ là đường cao của tứ diện

Xét tam giác đều $BCD$ có $BH = 2a \cdot \frac{{\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow BG = \frac{2}{3}BH = \frac{{2\sqrt 3 a}}{3}$.

Xét tam giác vuông $ABG$ có $AG = \sqrt {A{B^2} – B{G^2}} = \sqrt {{{(2a)}^2} – {{\left( {\frac{{2\sqrt 3 a}}{3}} \right)}^2}} = \frac{{2\sqrt 6 }}{3}a$.

Mà $d\left( {M;\left( {BCD} \right)} \right) = \frac{2}{3}d\left( {A;\left( {BCD} \right)} \right) = \frac{2}{3}AG = \frac{{4\sqrt 6 }}{9}a$.

Câu 13: Cho tứ diện đều $ABCD$ có cạnh bằng $a$. Khoảng cách từ $A$ đến mặt phẳng $\left( {BCD} \right)$ bằng:

A. $\frac{{a\sqrt 3 }}{4}$.

B. $\frac{{a\sqrt 3 }}{3}$.

C. $\frac{{a\sqrt 6 }}{3}$.

D. $\frac{{a\sqrt 6 }}{2}$.

Lời giải

Chọn C

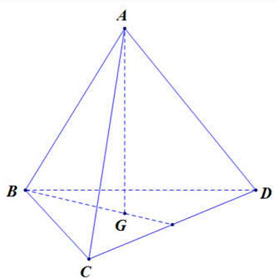
Gọi $G$ là trọng tâm tam giác $BCD$. Ta có $AG \bot \left( {BCD} \right)$ tại $G$ nên $d\left( {A,\left( {BCD} \right)} \right) = AG$.

Xét tam giác $ABG$ vuông tại $G$ có $AG = \sqrt {A{B^2} – B{G^2}} = \sqrt {{a^2} – {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}$.

Câu 14: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Đường thẳng $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ và $SA = a$. Tính khoảng cách $d$ giữa hai đường thẳng $SB$ và $CD$.

A. $d = 2a$.

B. $d = a\sqrt 3 $.

C. $d = a\sqrt 2 $.

D. $d = a$.

Lời giải

Chọn D

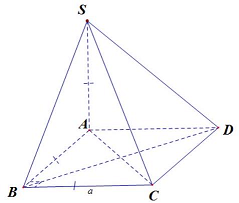
Vì $CD//AB$ nên $CD//\left( {SAB} \right)$. Do đó $d\left( {CD;SB} \right) = d\left( {CD;\left( {SAB} \right)} \right) = d\left( {D;\left( {SAB} \right)} \right) = DA = a$.

Câu 15: Cho hình chóp $S.ABCD$ có $SA$ vuông góc với mặt đáy và đáy $ABCD$ là hình chữ nhật. Biết $AB = 4a,AD = 3a,SB = 5a$. Tính khoảng cách từ điểm $C$ dến mặt phẳng $\left( {SBD} \right)$.

A. $\frac{{12\sqrt {41} a}}{{41}}$.

B. $\frac{{\sqrt {41} a}}{{12}}$.

C. $\frac{{12\sqrt {61} a}}{{61}}$.

D. $\frac{{\sqrt {61} a}}{{12}}$.

Lời giải

Chọn A

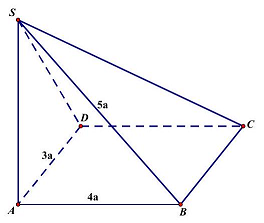
Ta có: $SA = \sqrt {S{B^2} – A{B^2}} = \sqrt {{{(5a)}^2} – {{(4a)}^2}} = 3a$.

Ta có $d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = h$.

Tứ diện $ASBD$ có các cạnh $AB,AD,AS$ đôi một vuông góc với nhau và $AB = 4a,AD = 3a,AS = 3a$ nên ta có

$\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{S^2}}}$

$ = \frac{1}{{16{a^2}}} + \frac{1}{{9{a^2}}} + \frac{1}{{9{a^2}}} = \frac{{41}}{{144{a^2}}} \Rightarrow h = \frac{{12a\sqrt {41} }}{{41}}$

Vậy $d\left( {C,\left( {SBD} \right)} \right) = \frac{{12a\sqrt {41} }}{{41}}$.

Câu 16: Cho tứ diện đều $ABCD$ có cạnh bằng $a$. Khoảng cách giữa hai đường thẳng $AB$ và $CD$ bằng

A. $\frac{{a\sqrt 2 }}{3}$.

B. $\frac{{a\sqrt 2 }}{2}$.

C. $\frac{{a\sqrt 3 }}{2}$.

D. $\frac{{a\sqrt 3 }}{3}$.

Lời giải

Chọn B

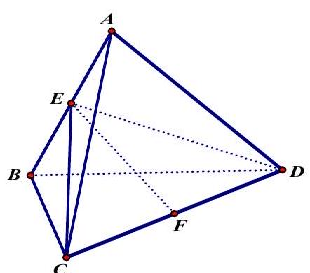
Gọi $E,F$ lần luợt là trung điểm của $AB$ và $CD$. Do tứ diện $ABCD$ đều cạnh $a$ nên $DE = CE = \frac{{a\sqrt 3 }}{2}$.Xét trong tam giác cân $ECD$ tại $E$ có $E{F^2} = E{D^2} – F{D^2} = \frac{{3{a^2}}}{4} – \frac{{{a^2}}}{4} = \frac{{{a^2}}}{2}$.

Do tam giác $ABC,ABD$ đều nên $ED \bot AB,EC \bot AB$ suy ra $EF \bot AB$ mà tam giác $ECD$ cân tại $E$ nên $EF \bot CD$. Vậy khoảng cách giữa $AB$ và $CD$ bằng độ dài đoạn $EF$. Tức bằng $\frac{{a\sqrt 2 }}{2}$.

Câu 17: Cho hình chóp $S.MNPQ$ có đáy là hình vuông, $MN = 3a$, với $0 < a \in \mathbb{R}$, biết $SM$ vuông góc với đáy, $SM = 6a$. Khoảng cách giữa hai đường thẳng $NP$ và $SQ$ bằng

A. $6a$.

B. $3a$.

C. $2a\sqrt 3 $.

D. $3a\sqrt 2 $.

Lời giải

Chọn B

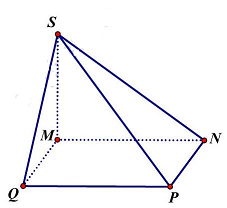
Do $MN \bot SM$ ( giả thiết $SM$ vuông góc với đáy) và $MN \bot MQ$ (do $MNPQ$ là hình vuông) vậy $MN \bot \left( {SMQ} \right)$ suy ra $d\left( {NP,SQ} \right) = d\left( {NP,\left( {SMQ} \right)} \right) = d\left( {N,\left( {SMQ} \right)} \right) = NM = 3a$.

Câu 18: Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật, $AB = a,BC = 2a,SA$ vuông góc với mặt phẳng đáy và $SA = a$. Khoảng cách giữa hai đường thẳng $BD,SC$ bằng

A. $\frac{{a\sqrt {30} }}{6}$.

B. $\frac{{4\sqrt {21} a}}{{21}}$.

C. $\frac{{2\sqrt {21} a}}{{21}}$.

D. $\frac{{a\sqrt {30} }}{{12}}$.

Lời giải

Chọn C

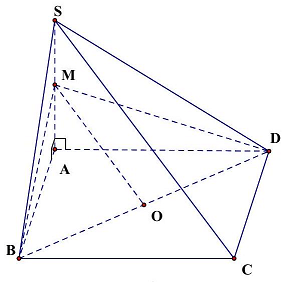
Gọi $O$ là tâm hình chữ nhật và $M$ là trung điểm $SA$, ta có: $SC//\left( {BMD} \right)$.

Do đó $d\left( {SC,BD} \right) = d\left( {SC,\left( {BMD} \right)} \right) = d\left( {S,\left( {BMD} \right)} \right) = d\left( {A,\left( {BMD} \right)} \right) = h$

Ta có: $AM,AB,AD$ đôi một vuông góc nên

$\frac{1}{{{h^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} = \frac{4}{{{a^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}}$

Suy ra: $h = \frac{{2a\sqrt {21} }}{{21}}$.

Câu 19: Cho hình chóp tứ giác $S.ABCD$ có đáy là hình chữ nhật cạnh $AD = 2a,SA \bot \left( {ABCD} \right)$ và $SA = a$. Khoảng cách giữa hai đường thẳng $AB$ và $SD$ bằng

A. $\frac{{a\sqrt 3 }}{3}$.

B. $\frac{{a\sqrt 6 }}{4}$.

C. $\frac{{2a\sqrt 5 }}{5}$.

D. $a\sqrt 6 $.

Lời giải

Chọn C

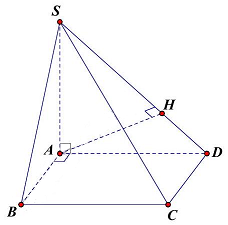
Trong tam giác $SAD$ kẻ đường cao $AH$ ta

có $AD \cdot AS = AH \cdot SD \Rightarrow AH = \frac{{AD \cdot AS}}{{SD}} = \frac{{2a \cdot a}}{{\sqrt {{{(2a)}^2} + {a^2}} }} = \frac{{2a\sqrt 5 }}{5}$

Dễ thấy $AH$ chính là đường vuông góc chung của $AB$ và $SD$

Vậy $d\left( {AB,SD} \right) = AH = \frac{{2a\sqrt 5 }}{5}$.

Câu 20: Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau và $OA = a,OB = OC = 2a$. Gọi $M$ là trung điểm của cạnh $BC$. Khoảng cách giữa hai đường thẳng $OM$ và $AC$ bằng:

A. $\frac{{a\sqrt 2 }}{2}$.

B. $\frac{{2a\sqrt 5 }}{5}$.

C. $a$.

D. $\frac{{a\sqrt 6 }}{3}$.

Lời giải

Chọn D

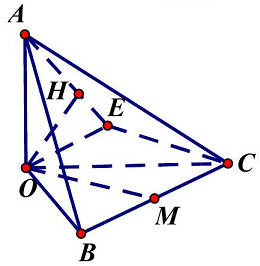
• Ta có được $OA \bot \left( {OBC} \right)$.

• Trong mặt phẳng $\left( {OBC} \right)$, dựng điểm $E$ sao cho $OMCE$ là hình bình hành thì $OMCE$ cũng là hình vuông (do $OBC$ là tam giác vuông cân tại $O$ ).

• Lại có: $\left\{ {\begin{array}{*{20}{l}}
{CE \bot OE} \\
{CE \bot OA}
\end{array} \Rightarrow CE \bot \left( {AOE} \right)} \right.$.

• Kẻ $OH \bot AE$ tại $H$ thì $OH \bot \left( {AEC} \right)$.

Vì $OM//\left( {AEC} \right)$ nên $d\left( {AC;OM} \right) = d\left( {O;\left( {ACE} \right)} \right) = OH = \frac{{OA \cdot OE}}{{\sqrt {O{A^2} + O{E^2}} }} = \frac{{a \cdot a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}$.

Câu 21: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông với đường chéo $AC = 2a,SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Khoảng cách giữa hai đường thẳng $SB$ và $CD$ là

A. $\frac{a}{{\sqrt 3 }}$.

B. $\frac{a}{{\sqrt 2 }}$.

C. $a\sqrt 2 $.

D. $a\sqrt 3 $.

Lời giải

Chọn C

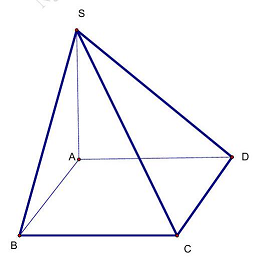
Ta có $\left\{ {\begin{array}{*{20}{l}}
{DA \bot SA} \\
{DA \bot AB}
\end{array} \Rightarrow DA \bot \left( {SAB} \right)} \right.$.

Mặt khác $\left\{ {\begin{array}{*{20}{l}}
{CD \not\subset \left( {SAB} \right)} \\
{CD//AB}
\end{array} \Rightarrow CD//\left( {SAB} \right)} \right.$.

Từ đó suy ra khoảng cách giữa $SB$ và $CD$ bằng khoảng cách giữa $\left( {SAB} \right)$ và $CD$ và bằng $DA$.

Từ giác $ABCD$ là hình vuông với đường chéo $AC = 2a$ suy ra $DA = \sqrt 2 a$.

Khoảng cách giữa hai đường thẳng $SB$ và $CD$ là $a\sqrt 2 $.

Câu 22: Cho tứ diện $ABCD$ có tam giác $ABD$ đều cạnh bằng 2 , tam giác $ABC$ vuông tại $B,BC = \sqrt 3 $. Biết khoảng cách giữa hai đường thẳng chéo nhau $AB$ và $CD$ bằng $\frac{{\sqrt {11} }}{2}$. Khi đó độ dài cạnh $CD$ là

A. $\sqrt 2 $.

B. 2 .

C. 1 .

D. $\sqrt 3 $.

Lời giải

Chọn A

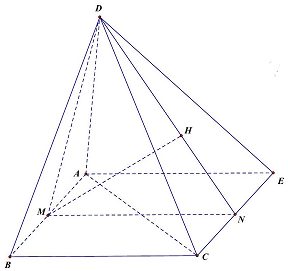
Dựng hình chữ nhật $ABCE$, gọi $M,N$ lần lượt là trung điểm $AB,CE,MH \bot DN$ tại $H$

Ta có

$\left\{ {\begin{array}{*{20}{l}}
{AB \bot DM} \\
{AB \bot MN}
\end{array} \Rightarrow AB \bot \left( {DMN} \right) \Rightarrow CE \bot \left( {DMN} \right) \Rightarrow MH \bot CE} \right.$

$\left\{ {\begin{array}{*{20}{l}}
{MH \bot DN} \\
{MH \bot CE}
\end{array} \Rightarrow MH \bot \left( {CDE} \right)} \right.$ tại $H$

$ \Rightarrow d\left( {AB,CD} \right) = d\left[ {M;\left( {CDE} \right)} \right] = MH = \frac{{\sqrt {11} }}{2}$

Tam giác $DMN$ có $DM = MN = \sqrt 3 \Rightarrow H$ là trung điểm $DN$, mà $HN = \sqrt {M{N^2} – M{H^2}} = \frac{1}{2}$

$ \Rightarrow DN = 1$

Xét tam giác $DNC$ vuông tại $N\;$: $CD = \sqrt {D{N^2} + C{N^2}} = \sqrt 2 $.

Câu 23: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a,SA \bot \left( {ABCD} \right),SA = a\sqrt 3 $. Gọi $M$ là trung điểm $SD$. Tính khoảng cách giữa đường thẳng $AB$ và $CM$.

A. $\frac{{2a\sqrt 3 }}{3}$.

B. $\frac{{a\sqrt 3 }}{2}$.

C. $\frac{{3a}}{4}$.

D. $\frac{{a\sqrt 3 }}{4}$.

Lời giải

Chọn B

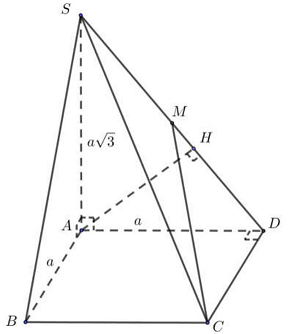
*) Trong tam giác $\vartriangle SAD$, kẻ đường cao $AH \Rightarrow AH \bot SD$ (1).

$CD \bot AD$

$CD \bot SA \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AH\left( 2 \right)$.

Từ (1), (2) $ \Rightarrow AH \bot \left( {SCD} \right)$.

Có $AB//CD \Rightarrow AB//\left( {SCD} \right)$, mà

$CM \subset \left( {SCD} \right) \Rightarrow d\left( {AB,CM} \right) = d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right) = AH$.

*) $\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}} \Rightarrow AH = \frac{{a\sqrt 3 }}{2}$.

Dạng 2. Tính khoảng cách liên quan đến hình lăng trụ, hình hộp

Câu 24: Cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$ có $AD = 2a,CD = a,AA’ = a\sqrt 2 $. Đường chéo $AC’$ có độ dài bằng

A. $a\sqrt 5 $.

B. $a\sqrt 7 $.

C. $a\sqrt 6 $.

D. $a\sqrt 3 $.

Lời giải

Chọn B

$AC’ = \sqrt {A{B^2} + A{D^2} + A{A^{‘2}}} = \sqrt {{a^2} + {{(2a)}^2} + {{(a\sqrt 2 )}^2}} = a\sqrt 7 $.

Câu 25: Cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$ có $AD = 2a,CD = a,AA’ = a\sqrt 2 $. Đường chéo $AC’$ có độ dài bằng:

A. $a\sqrt 5 $.

B. $a\sqrt 7 $.

C. $a\sqrt 6 $.

D. $a\sqrt 3 $.

Lời giải

Chọn B

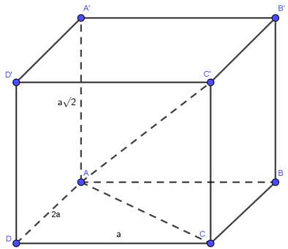
Ta có $AC = \sqrt {A{D^2} + D{C^2}} = a\sqrt 5 $.

Nên $AC’ = \sqrt {A{C^2} + C{C^{‘2}}} = \sqrt {5{a^2} + 2{a^2}} = a\sqrt 7 $.

Câu 26: Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng 1 . Tính khoảng cách $d$ từ điểm $A$ đến mặt phẳng $\left( {BDA’} \right)$.

A. $d = \frac{{\sqrt 3 }}{3}$.

B. $d = \frac{{\sqrt 6 }}{4}$.

C. $d = \frac{{\sqrt 2 }}{2}$.

D. $d = \sqrt 3 $.

Lời giải

Chọn A

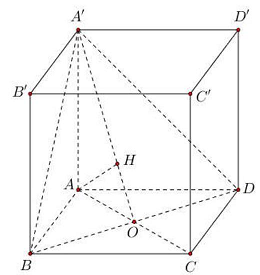
Gọi $O$ là tâm của hình vuông $ABCD$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{BD \bot AO} \\
{BD \bot AA’}
\end{array} \Rightarrow BD \bot \left( {AA’O} \right)} \right.$

Suy ra $\left( {BDA’} \right) \bot \left( {AA’O} \right)$.

Kẻ $AH \bot A’O \Rightarrow AH \bot \left( {BDA’} \right)$.

Suy ra $AH = d\left( {A,\left( {BDA’} \right)} \right)$.

Xét tam giác $AA’O$ vuông tại $A$ có $AA’ = 1,AO = \frac{1}{2}AC = \frac{{\sqrt 2 }}{2}:AH = \frac{{AA’ \cdot AO}}{{\sqrt {A{A^{‘2}} + A{O^2}} }} = \frac{{\sqrt 3 }}{3}$.

Vậy $d\left( {A,\left( {BDA’} \right)} \right) = \frac{{\sqrt 3 }}{3}$.

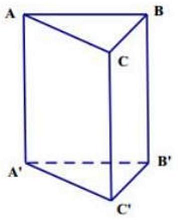
Câu 27: Cho hình lăng trụ đứng $ABCA’B’C’$ có đáy là tam giác $ABC$ vuông tại $A$ có $BC = 2a,AB = a\sqrt 3 $, (tham khảo hình vẽ bên). Khoảng cách từ $A$ đến mặt phẳng ( $\left. {BCC’B’} \right)$ là

A. $\frac{{a\sqrt 5 }}{2}$.

B. $\frac{{a\sqrt 7 }}{3}$.

C. $\frac{{a\sqrt 3 }}{2}$.

D. $\frac{{a\sqrt {21} }}{7}$.

Lời giải

Chọn C

Vì lăng trụ $ABCA’B’C’$ là lăng trụ đứng nên $\left( {ABC} \right) \bot \left( {BCC’B’} \right)$.

Do đó kẻ $AH \bot BC \Rightarrow AH \bot \left( {BCC’B’} \right)$.

Vậy khoảng cách từ $A$ đến mặt phẳng $\left( {BCC’B’} \right)$ là đoạn $AH$.

Ta có $AC = \sqrt {4{a^2} – 3{a^2}} = a$.

$\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}} \Rightarrow AH = \frac{{\sqrt 3 a}}{2}$.

Câu 28: Cho hình lăng trụ $ABC \cdot A’B’C’$ có tất cả các cạnh đều bằng $a$. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng ${30^ \circ }$. Hình chiếu $H$ của $A$ trên mặt phẳng $\left( {A’B’C’} \right)$ là trung điểm của $B’C’$. Tính theo $a$ khoảng cách giữa hai mặt phẳng đáy của lăng trụ $ABC \cdot A’B’C’$.

A. $\frac{a}{2}$.

B. $\frac{a}{3}$.

C. $\frac{{a\sqrt 3 }}{2}$.

D. $\frac{{a\sqrt 2 }}{2}$.

Lời giải

Chọn A.

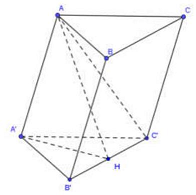
Góc tạo bởi cạnh bên và mặt phẳng đáy bằng ${30^ \circ }$ nên $\widehat {AA’H} = {30^ \circ }$.

Khoảng cách giữa hai mặt phẳng đáy của lăng trụ $ABC \cdot A’B’C’$ bằng

$AH = AA’.sin\widehat {AA’H} = AA’.sin{30^ \circ } = \frac{a}{2}$.

Câu 29: Cho hình lập phương $ABCD \cdot A’B’C’D’$ cạnh $a$. Tính khoảng cách giữa hai đường thẳng $AB’$ và $CD’$.

A. $\frac{{a\sqrt 2 }}{2}$.

B. $a$.

C. $a\sqrt 2 $.

D. $2a$.

Lời giải

Chọn B

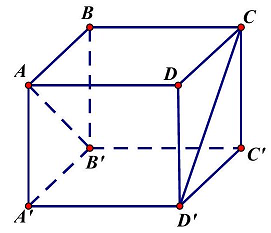
• Do $AB’//\left( {CDD’C’} \right)$ nên ta có:

$d\left( {AB’;CD’} \right) = d\left( {AB’;\left( {CDD’C’} \right)} \right) = d\left( {A;\left( {CDD’C’} \right)} \right) = AD = a$

Câu 30: Cho hình hộp chữ nhật $EFGH \cdot E’F’G’H’$ có $EF = 3a,EH = 4a,EE’ = 12a$, với $0 < a \in \mathbb{R}$. Khoảng cách giữa hai đường thẳng $EF’$ và $GH’$ bằng

A. $12a$.

B. $3a$.

C. $2a$.

D. $4a$.

Lời giải

Chọn D

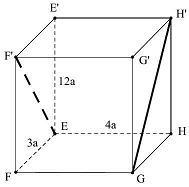
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{EF’ \subset \left( {EFF’E’} \right)} \\
{GH’ \subset \left( {GHH’G’} \right)} \\
{\left( {EFF’E’} \right)//\left( {GHH’G’} \right)}
\end{array} \Rightarrow d\left( {EF’,GH’} \right) = d\left( {\left( {EFF’E’} \right),\left( {GHH’G’} \right)} \right) = d\left( {E,\left( {GHH’G’} \right)} \right)} \right.$.

Vì $EH \bot \left( {GHH’G’} \right) \Rightarrow d\left( {E,\left( {GHH’G’} \right)} \right) = EH = 4a$.

Câu 31: Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng $a$. Khoảng cách giữa hai đường thẳng $BB’$ và $A’C’$ bằng

A. $a\sqrt 2 $.

B. $a$.

C. $a\sqrt 3 $.

D. $\frac{{a\sqrt 2 }}{2}$.

Lời giải

Chọn D

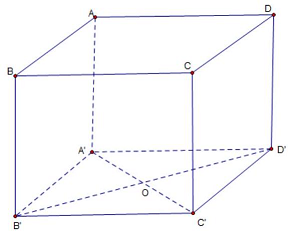
Gọi $O = A’C’ \cap B’D’$.

Ta có $BB’ \bot B’O,A’C’ \bot B’O \Rightarrow B’O = d\left( {BB’,A’C’} \right)$.

$B’O = \frac{1}{2}B’D’ = \frac{1}{2}\sqrt {B'{C^{‘2}} + C'{D^{‘2}}} = \frac{{a\sqrt 2 }}{2}$.

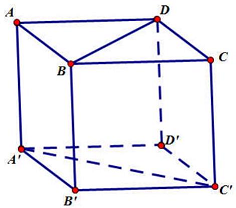
Câu 32: Cho lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng $a$ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng $BD$ và $A’C’$ bằng

A. $\sqrt 3 a$.

B. $a$.

C. $\frac{{\sqrt 3 a}}{2}$.

D. $\sqrt 2 a$.

Lời giải

Chọn B

Ta có khoảng cách giữa hai đường thẳng chéo nhau $BD$ và $A’C’$ bằng khoảng cách giữa mặt phẳng song song $\left( {ABCD} \right)$ và $\left( {A’B’C’D’} \right)$ thứ tự chứa $BD$ và $A’C’$. Do đó khoảng cách giữa hai đường thẳng $BD$ và $A’C’$ bằng $a$.

Câu 33: Cho lăng trụ tam giác đều $ABC \cdot A’B’C’$ có $AB = a,AA’ = 2a$. Khoảng cách giữa $AB’$ và $CC’$ bằng

A. $\frac{{2a\sqrt 5 }}{5}$.

B. $a$.

C. $a\sqrt 3 $.

D. $\frac{{a\sqrt 3 }}{2}$.

Lời giải

Chọn D

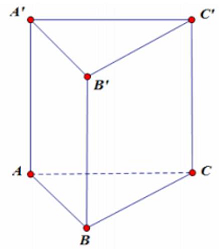
Gọi $I$ là trung điểm của $AB$.

Ta có: $CC’//BB’$ nên $CC’//\left( {ABB’A’} \right)$.

Vì $AB’ \subset \left( {ABB’A’} \right)$ nên $d\left( {CC’,AB’} \right) = d\left( {CC’,\left( {ABB’A’} \right)} \right) = CI$.

Do lăng trụ tam giác đều $ABC \cdot A’B’C’$ nên tam giác $ABC$ đều cạnh $a$ nên $CI = \frac{{a\sqrt 3 }}{2}$.

Nên $d\left( {CC’,AB’} \right) = CI = \frac{{a\sqrt 3 }}{2}$.