50 Câu Trắc Nghiệm Góc Giữa Đường Thẳng Và Mặt Phẳng Mức Vận Dụng

50 câu trắc nghiệm góc giữa đường thẳng và mặt phẳng mức vận dụng giải chi tiết được soạn dưới dạng file word và PDF gồm 10 trang. Các bạn xem và tải về ở dưới.
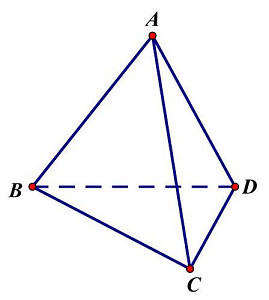
Câu 1: Cho tứ diện đều $ABCD$. Gọi $\varphi $ là góc giữa đường thẳng $AB$ và mặt phẳng $\left( {BCD} \right)$. Tính $cos\varphi $.

A. $cos\varphi = 0$.

B. $cos\varphi = \frac{1}{2}$.

C. $cos\varphi = \frac{{\sqrt 3 }}{3}$.

D. $cos\varphi = \frac{{\sqrt 2 }}{3}$.

Lời giải

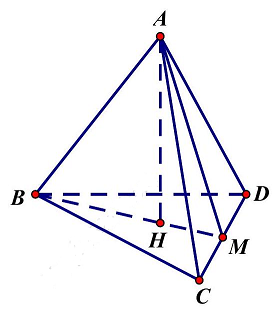
Gọi $M$ là trung điểm của $CD$. Ta có $BM = \frac{{AB\sqrt 3 }}{2}$.

Gọi $H$ là chân đường cao hạ từ $A$ xuống mặt phẳng $\left( {BCD} \right)$ thì $H \in BM$ và $BH = \frac{2}{3}BM = \frac{{AB\sqrt 3 }}{3}$

Góc giữa đường thẳng $AB$ và mặt phẳng $\left( {BCD} \right)$ là $\widehat {ABM}$.

Ta có $cos\varphi = cos\widehat {ABM} = \frac{{BH}}{{AB}} = \frac{{\frac{{AB\sqrt 3 }}{3}}}{{AB}} = \frac{{\sqrt 3 }}{3}$.

Câu 2: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $\sqrt 2 a$. Độ lớn của góc giữa đường thẳng $SA$ và mặt phẳng đáy bằng

A. ${45^ \circ }$.

B. ${75^ \circ }$.

C. ${30^ \circ }$.

D. ${60^ \circ }$.

Lời giải

Chọn D

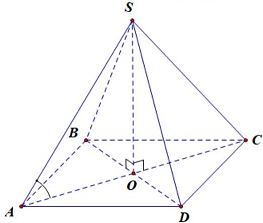
Gọi $O$ là tâm của hình vuông $ABCD$, ta có $SO \bot \left( {ABCD} \right)$.

$\left( {\widehat {SA,\left( {ABCD} \right)}} \right) = \widehat {\left( {SA,AO} \right)} = \widehat {SAO} = \alpha $.

Ta có $OA = \frac{1}{2}AC = \frac{1}{2}\sqrt {A{B^2} + B{C^2}} = \frac{{a\sqrt 2 }}{2}$.

$\vartriangle SAO$ vuông tại $O$ có $cos\alpha = \frac{{OA}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 2 }} = \frac{1}{2}$ suy ra $\alpha = {60^ \circ }$.

Vậy góc giữa $SA$ và $\left( {ABCD} \right)$ bằng ${60^ \circ }$.

Câu 3: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $3a,SA$ vuông góc với mặt phẳng đáy, $SB = 5a$. Tính sin của góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$.

A. $\frac{{2\sqrt 2 }}{3}$.

B. $\frac{{3\sqrt 2 }}{4}$.

C. $\frac{{3\sqrt {17} }}{{17}}$.

D. $\frac{{2\sqrt {34} }}{{17}}$.

Lời giải

Chọn D

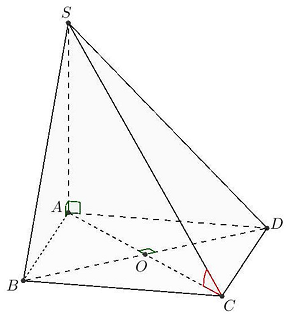
$ABCD$ là hình vuông cạnh $3a$ nên $AC = 3a\sqrt 2 $

Xét tam giác $SAB$ vuông tại $A:SA = \sqrt {S{B^2} – A{B^2}} = 4a$

$SA \bot \left( {ABCD} \right) \Rightarrow \left( {\widehat {SC,\left( {ABCD} \right)}} \right) = \widehat {SCA}$

Xét tam giác $SAC$ vuông tại $A$ :

$SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt {34} $

$sin\widehat {SCA} = \frac{{SA}}{{SC}} = \frac{{2\sqrt {34} }}{{17}}$

Câu 4: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = 2a,AD = a.SA$ vuông góc với mặt phẳng đáy. $SA = a\sqrt 3 $. Cosin của góc giữa $SC$ và mặt đáy bằng:

A. $\frac{{\sqrt 5 }}{4}$.

B. $\frac{{\sqrt 7 }}{4}$.

C. $\frac{{\sqrt 6 }}{4}$.

D. $\frac{{\sqrt {10} }}{4}$.

Lời giải

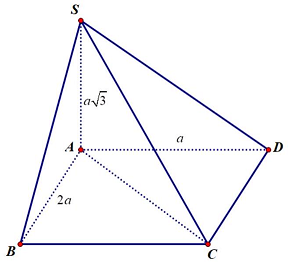
Hình chiếu của $SC$ lên $\left( {ABCD} \right)$ là $AC$

Do đó $\left[ {\widehat {SC,\left( {ABCD} \right)}} \right] = \widehat {SCA}$

$AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {4{a^2} + {a^2}} = a\sqrt 5 \Rightarrow SC = 2a\sqrt 2 $

Trong tam giác vuông $SAC:cos\widehat {SCA} = \frac{{AC}}{{SC}} = \frac{{a\sqrt 5 }}{{2a\sqrt 2 }} = \frac{{\sqrt {10} }}{4}$.

Câu 5: Cho hình chóp $S.ABCD$, đáy $ABCD$ là hình vuông cạnh $a$ và $SA \bot \left( {ABCD} \right)$. Biết $SA = \frac{{a\sqrt 6 }}{3}$. Góc giữa $SC$ và $\left( {ABCD} \right)$ là:

A. ${45^ \circ }$.

B. ${30^ \circ }$.

C. ${75^ \circ }$.

D. ${60^ \circ }$.

Lời giải

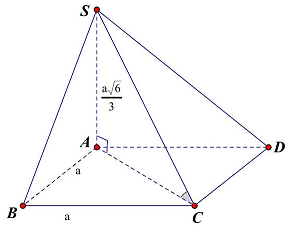
Ta có: $SA \bot \left( {ABCD} \right)$.

Do đó $AC$ là hình chiếu của $SC$ lên $\left( {ABCD} \right)$.

$ \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}$

Xét tam giác $SAC$ vuông tại $A$ có tan $\widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{\frac{{a\sqrt 6 }}{3}}}{{a\sqrt 2 }} = \frac{{\sqrt 3 }}{3}$.

$ \Rightarrow \widehat {SCA} = {30^ \circ }$.

Vậy góc giữa $SC$ và $\left( {ABCD} \right)$ là ${30^ \circ }$.

Câu 6: Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, Tam giác $SAB$ cân tại $S$ và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích của khối chóp $S.ABCD$ là $\frac{{{a^3}\sqrt {15} }}{6}$. Góc giữa đường thẳng $SC$ và mặt phẳng đáy $\left( {ABCD} \right)$ là

A. ${120^ \circ }$.

B. ${30^ \circ }$.

C. ${45^ \circ }$.

D. ${60^ \circ }$.

Lời giải

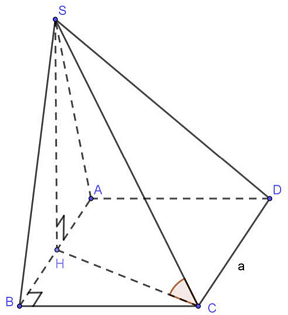
Gọi $H$ là trung điểm $AB$. Ta có $SH \bot \left( {ABCD} \right)$.

$\begin{array}{*{20}{r}}
{}&{{S_{ABCD}} = {a^2}.} \\
{}&{V = \frac{1}{3}{S_{ABCD}}.SH \Rightarrow SH = \frac{{3V}}{{{S_{ABCD}}}} = \frac{{a\sqrt {15} }}{2}.} \\
{}&{CH = \sqrt {A{C^2} + A{H^2}} = \frac{{a\sqrt 5 }}{2}.} \\
{}&{\widehat {\left( {SC,\left( {ABCD} \right)} \right)} = \widehat {\left( {SC,CH} \right)}.} \\
{}&{tan\widehat {SCH} = \frac{{SH}}{{CH}} = \sqrt 3 .}
\end{array}$

Vậy $\overline {\left( {SC,\left( {ABCD} \right)} \right)} = {60^ \circ }$

Câu 7: Cho hình lăng trụ đều $ABC \cdot A’B’C’$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm của $AB$ và $\alpha $ là góc tạo bởi đường thẳng $MC’$ và mặt phẳng $\left( {ABC} \right)$. Khi đó tan $\alpha $ bằng

A. $\frac{{2\sqrt 7 }}{7}$.

B. $\frac{{\sqrt 3 }}{2}$.

C. $\sqrt {\frac{3}{7}} $.

D. $\frac{{2\sqrt 3 }}{3}$.

Lời giải

Ta có $MC$ là hình chiếu của $MC’$ lên $\left( {ABC} \right)$. Suy ra $\alpha = C’CM$.

Xét tam giác $MCC’$ vuông tại $C$ có: $tan\alpha = \frac{{CC’}}{{CM}} = \frac{a}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{2\sqrt 3 }}{3}$.

Câu 8: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $S$ lên $\left( {ABC} \right)$ trùng với trung điểm $H$ của cạnh $BC$. Biết tam giác $SBC$ là tam giác đều. Tính số đo của góc giữa $SA$ và $\left( {ABC} \right)$.

A. ${30^ \circ }$.

B. ${75^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Lời giải

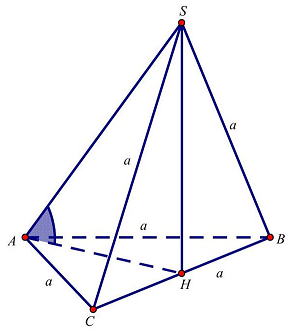
Dễ thấy $AH$ là hình chiếu vuông góc của $SA$ lên mặt phẳng đáy.

Do đó góc tạo bởi $SA$ và $\left( {ABC} \right)$ là $\widehat {SAH}$.

Mặt khác, $\vartriangle ABC = \vartriangle SBC \Rightarrow SH = AH = \frac{{a\sqrt 3 }}{2}$. Vậy tam giác $SAH$ là tam giác vuông cân đỉnh $H$ hay $\widehat {SAH} = {45^ \circ }$.

Câu 9: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$. Tam giác $SBC$ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Số đo góc giữa đường thẳng $SA$ và $\left( {ABC} \right)$ bằng:

A. ${45^ \circ }$.

B. ${30^ \circ }$.

C. ${75^ \circ }$.

D. ${60^ \circ }$.

Lời giải

Chọn D

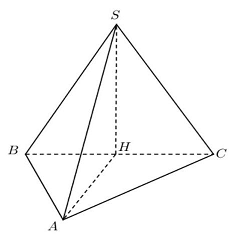
Gọi $H$ là trung điểm cạnh $BC \Rightarrow SH \bot BC;SH = \frac{{BC\sqrt 3 }}{2}$ ( $\vartriangle SBC$ đều)

$\left\{ {\begin{array}{*{20}{l}}
{\left( {SBC} \right) \bot \left( {ABC} \right)} \\
{\left( {SBC} \right) \cap \left( {ABC} \right) = BC \Rightarrow SH \bot \left( {ABC} \right)} \\
{SH \bot AB;SH \in \left( {SBC} \right)}
\end{array}} \right.$

$ \Rightarrow \left( {\widehat {SA;\left( {ABC} \right)}} \right) = \left( {\widehat {SA;AH}} \right) = \widehat {SAH}$

$\vartriangle ABC$ vuông tại $A;H$ là trung điểm $BC \Rightarrow AH = \frac{{BC}}{2}$

$\vartriangle SAH$ vuông tại $H \Rightarrow tan\widehat {SAH} = \frac{{SH}}{{AH}} = \frac{{\frac{{BC \cdot \sqrt 3 }}{2}}}{{\frac{{BC}}{2}}} = \sqrt 3 \Rightarrow \widehat {SAH} = {60^ \circ }$.

Câu 10: Cho hình chóp $S.ABC$ có $SA,SB,SC$ đôi một vuông góc với nhau và $SA = SB = SC = a$. sin của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABC} \right)$ bằng

A. $\frac{{\sqrt 6 }}{3}$.

B. $\frac{{\sqrt 2 }}{2}$.

C. $\frac{1}{{\sqrt 3 }}$.

D. $\frac{2}{{\sqrt 6 }}$.

Lời giải

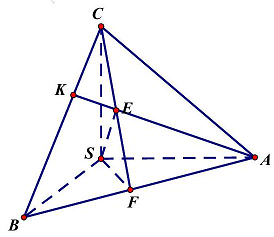
Trong tam giác $ABC$ kẻ đường cao $AK$ và $CF$ và $AK \cap CF = \left\{ E \right\}$ nên $E$ là trực tâm tam giác $ABC$.

$\left\{ {\begin{array}{*{20}{l}}
{SC \bot SA} \\
{SC \bot SB}
\end{array} \Rightarrow SC \bot \left( {SAB} \right)} \right.$ hay $SC \bot AB$

Mà $CF \bot AB$ nên $AB \bot \left( {SCF} \right) \Rightarrow AB \bot SE$. Chứng minh tương tự ta được $BC \bot \left( {SAK} \right)$

$ \Rightarrow BC \bot SE$. Vậy $SE \bot \left( {ABC} \right)$.

Ta có $CE$ là hình chiếu của $SC$ lên mặt phẳng $\left( {ABC} \right)$.

$\left( {SC,\left( {ABC} \right)} \right) = \left( {SC,CE} \right) = \widehat {SCE}$

Ta có tam giác $SCF$ vuông tại $S$ nên $\frac{1}{{S{E^2}}} = \frac{1}{{S{C^2}}} + \frac{1}{{S{F^2}}}$. Mặt khác tam giác $SAB$ vuông tại $S$ nên $\frac{1}{{S{F^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}}$. Suy ra $\frac{1}{{S{E^2}}} = \frac{1}{{S{C^2}}} + \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} \Leftrightarrow \frac{1}{{S{E^2}}} = \frac{3}{{{a^2}}} \Leftrightarrow SE = \frac{a}{{\sqrt 3 }}$.

$sin\widehat {SCE} = \frac{{SE}}{{SC}} = \frac{a}{{\sqrt 3 }}:a = \frac{1}{{\sqrt 3 }}$.

Câu 11: Cho hình chóp $S.ABCD$ có tất cả các cạnh đều bằng nhau. Gọi $E,F$ lần lượt là trung điểm của $SB$ và $SD,O$ là giao điểm của $AC$ và $BD$. Khẳng định nào sau đây sai?

A. $SO \bot \left( {ABCD} \right)$.

B. $\left( {SAC} \right) \bot \left( {SBD} \right)$.

C. $EF//\left( {ABCD} \right)$.

D. $\left( {\overline {SA,\left( {ABCD} \right)} } \right) = {60^ \circ }$.

Lời giải

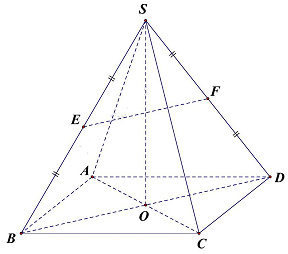
Ta có:

$ + S.ABCD$ là hình chóp đều $ \Rightarrow SO \bot \left( {ABCD} \right)$.

$ + \left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SO}
\end{array} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {SBD} \right) \bot \left( {SAC} \right)} \right.$.

$ + EF//BD \Rightarrow EF//\left( {ABCD} \right)$.

$ + \left( {\widehat {SA,\left( {ABCD} \right)}} \right) = \left( {\widehat {SA,AO}} \right) = \widehat {SAO} = {45^ \circ }$.

Câu 12: Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a$. Hình chiếu vuông góc của $S$ lên $\left( {ABC} \right)$ là trung điểm của cạnh $BC$. Biết $\vartriangle SBC$ đều, tính góc giữa $SA$ và $\left( {ABC} \right)$

A. ${45^ \circ }$

B. ${90^ \circ }$

C. ${30^ \circ }$

D. ${60^ \circ }$

Lời giải

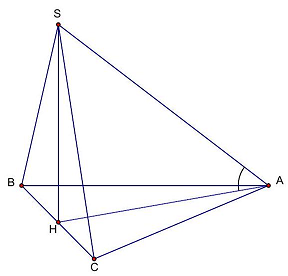
Gọi $H$ là trung điểm của $BC$ suy ra $SH \bot \left( {ABC} \right)$

Do đó hình chiếu của $SA$ lên mặt phẳng $\left( {ABC} \right)$ là $AH$

Do $\vartriangle ABC$ và $\vartriangle SBC$ dều cạnh $a$ nên $SH = AH \Rightarrow \vartriangle SAH$ vuông cân tại $H$

$ \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \widehat {SAH} = {45^ \circ }$.

Câu 13: Cho hình lăng trụ $ABC \cdot A’B’C’$, đáy $ABC$ là tam giác vuông tại $B,AB = a,\widehat {ACB} = {30^ \circ }.M$ là trung điểm $AC$. Hình chiếu vuông góc của đỉnh $A’$ lên mặt phẳng $\left( {ABC} \right)$ là trung điểm $H$ của $BM$.

Khoảng cách từ $C’$ đến mặt phẳng $\left( {BMB’} \right)$ bằng $\frac{{3a}}{4}$. Tính số đo góc tạo bởi cạnh bên và mặt phẳng đáy của hình lăng trụ.

A. ${60^ \circ }$.

B. ${30^ \circ }$.

C. ${90^ \circ }$.

D. ${45^ \circ }$.

Lời giải

Chọn A

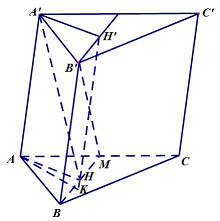
Ta có: $d\left( {C’,\left( {BMB’} \right)} \right) = d\left( {C,\left( {BMB’} \right)} \right) = d\left( {A,\left( {BMB’} \right)} \right) = \frac{{3a}}{4}$,

Trong tam giác $ABC$ có: $AC = 2a,BM = a,AM = a$ suy ra tam giác $ABM$ là tam giác đều cạnh $a$. Dựng hình bình hành $AA’H’H$ suy ra $H’ \in \left( {BMB’} \right),K$ là hình chiếu của $A$ lên $H’H$.

$\left\{ {\begin{array}{*{20}{l}}
{BM \bot AH} \\
{BM \bot A’H}
\end{array} \Rightarrow BM \bot \left( {AA’H’H} \right) \Rightarrow BM \bot AK.} \right.$

$\left\{ {\begin{array}{*{20}{l}}
{AK \bot BM} \\
{AK \bot HH’}
\end{array} \Rightarrow AK \bot \left( {BMB’} \right) \Rightarrow d\left( {A,\left( {BMB’} \right)} \right) = AK = \frac{{3a}}{4}} \right.$.

Trong hình bình hành $AA’H’H$ ta có $AK.HH’ = A’H.AH \Rightarrow \frac{{A’H}}{{HH’}} = \frac{{AK}}{{AH}} = \frac{{3a}}{4} \cdot \frac{2}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{2}$.

Mặt khác: $\widehat {\left( {AA’,\left( {ABC} \right)} \right)} = \widehat {\left( {AA’,AH} \right)} = \widehat {A’AH}$.

Trong tam giác vuông $AA’H$ có $sin\widehat {AA’H} = \frac{{A’H}}{{AA’}} = \frac{{A’H}}{{HH’}} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {AA’H} = {60^ \circ }$.

Câu 14: Cho hình chóp $S.ABCD$ có đáy là hình thoi tâm $O,SO \bot \left( {ABCD} \right)$. Góc giữa $SA$ và mặt phẳng $\left( {SBD} \right)$ là góc

A. $\widehat {ASO}$.

B. $\widehat {SAO}$.

C. $\widehat {SAC}$.

D. $\widehat {ASB}$.

Lời giải

Chọn A

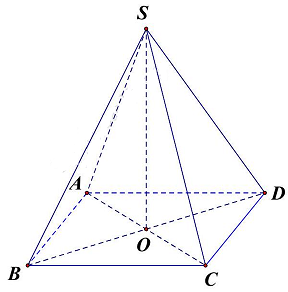
Vì $ABCD$ là hình thoi $ \Rightarrow AO \bot BD$.

Mà $AO \bot SO$ do $SO \bot \left( {ABCD} \right)$. Suy ra $AO \bot \left( {SBD} \right)$ hay $O$ là hình chiếu của $A$ lên $\left( {SBD} \right)$.

Suy ra góc giữa $SA$ và mặt phẳng $\left( {SBD} \right)$ là góc $\widehat {ASO}\left( {\widehat {ASO} < {{90}^ \circ }} \right.$ do $\vartriangle SAO$ vuông ở $O$ ).

Câu 15: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 $. Tìm số đo của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$.

A. ${45^ \circ }$.

B. ${30^ \circ }$.

C. ${90^ \circ }$.

D. ${60^ \circ }$.

Lời giải

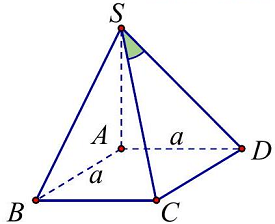
Dễ thấy $CB \bot \left( {SAB} \right) \Rightarrow SB$ là hình chiếu vuông góc của $SC$ lên $\left( {SAB} \right)$.

Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là $\widehat {CSB}$.

Tam giác $CSB$ có $\hat B = {90^ \circ };CB = a;SB = a\sqrt 3 \Rightarrow tan\widehat {CSB} = \frac{{CB}}{{SB}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}$.

Vậy $\widehat {CSB} = {30^ \circ }$.

Câu 16: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a,SA \bot \left( {ABCD} \right)$ và $SA = a\sqrt 3 $ Gọi $\alpha $ là góc tạo bởi giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$, khi đó $\alpha $ thỏa mãn hệ thức nào sau đây:

A. $cos\alpha = \frac{{\sqrt 2 }}{8}$.

B. $sin\alpha = \frac{{\sqrt 2 }}{8}$.

C. $sin\alpha = \frac{{\sqrt 2 }}{4}$.

D. $cos\alpha = \frac{{\sqrt 2 }}{4}$.

Gọi $O$ là tâm của đáy $ABCD$.

Lời giải

Ta có $BO \bot AC$ và $BO \bot SA$ nên $SO$ là hình chiếu của $SB$ trên $\left( {SAC} \right)$.

Suy ra $\alpha = \widehat {BSO}$.

Lại có $BO = \frac{{a\sqrt 2 }}{2},SB = \sqrt {S{A^2} + A{B^2}} = 2a$. Suy ra $sin\alpha = \frac{{BO}}{{SB}} = \frac{{\sqrt 2 }}{4}$.

Câu 17: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a.SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ và $SA = a\sqrt 6 $ (hình vẽ). Gọi $\alpha $ là góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$. Tính $sin\alpha $ ta được kết quả là:

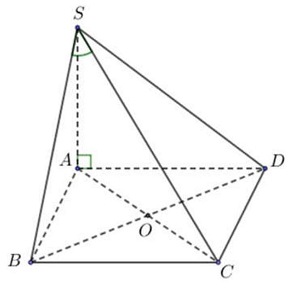
A. $\frac{1}{{\sqrt {14} }}$.

B. $\frac{{\sqrt 2 }}{2}$.

C. $\frac{{\sqrt 3 }}{2}$.

D. $\frac{1}{5}$.

Lời giải

Gọi $O$ là tâm hình vuông $ABCD$ thì $BO \bot \left( {SAC} \right) \Rightarrow \alpha = \widehat {\left( {SB,\left( {SAC} \right)} \right)} = \widehat {BSO}$.

Ta có $SB = a\sqrt 7 ,sin\alpha = \frac{{BO}}{{SB}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 7 }} = \frac{1}{{\sqrt {14} }}$.

Câu 18: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, cạnh $AB = a,AD = \sqrt 3 a$. Cạnh bên $SA = a\sqrt 2 $ và vuông góc mặt phẳng đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$ bằng:

A. ${75^ \circ }$.

B. ${60^ \circ }$.

C. ${45^ \circ }$.

D. ${30^ \circ }$.

Lời giải

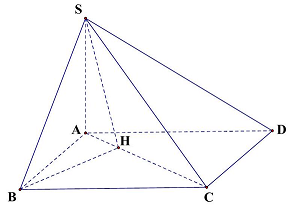
Kẻ $BH \bot AC$ và $H \in AC \Rightarrow BH \bot \left( {SAC} \right)$.

$SH$ là hình chiếu của $BH$ trên mặt phẳng $\left( {SAC} \right)$.

Góc giữa $SB$ và mặt phẳng $\left( {SAC} \right)$ là $\widehat {BSH}$.

Ta có $BH = \frac{{AB \cdot BC}}{{\sqrt {A{B^2} + B{C^2}} }} = \frac{{a\sqrt 3 }}{2},SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 3 $.

Trong tam giác vuông $SBH$ ta có $sin\widehat {BSH} = \frac{{BH}}{{SB}} = \frac{1}{2} \Rightarrow \widehat {BSH} = {30^ \circ }$.

Câu 19: Cho hình lăng trụ đứng $ABC \cdot A’B’C’$ có đáy $ABC$ là tam giác vuông tại $B,AB = BC = a$, $BB’ = a\sqrt 3 $. Tính góc giữa đường thẳng $A’B$ và mặt phẳng $\left( {BCC’B’} \right)$.

A. ${45^ \circ }$.

B. ${30^ \circ }$.

C. ${60^ \circ }$.

D. ${90^ \circ }$.

Lời giải

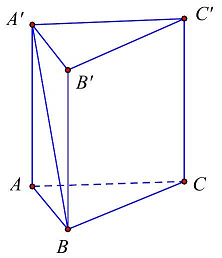
Hình lăng trụ đứng $ABC \cdot A’B’C’$ nên $BB’ \bot \left( {A’B’C’} \right) \Rightarrow BB’ \bot A’B’ \Rightarrow A’B’ \bot BB’$ (1)

Bài ra có $AB \bot BC \Rightarrow A’B’ \bot B’C’$.

Kết hợp với $\left( 1 \right) \Rightarrow A’B’ \bot \left( {BCC’B’} \right) \Rightarrow \widehat {\left( {A’B;\left( {BCC’B’} \right)} \right)} = \widehat {A’BB’}$

$ \Rightarrow tan\left( {\widehat {\left. {A’B;\left( {BCC’B’} \right)} \right)} = tan\widehat {A’BB’} = \frac{{A’B’}}{{BB’}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {\left( {A’B;\left( {BCC’B’} \right)} \right)} = {{30}^ \circ }} \right.$.

Câu 20: Cho khối chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, tam giác $ABC$ vuông tại $B,AC = 2a,BC = a$, $SB = 2a\sqrt 3 $. Tính góc giữa $SA$ và mặt phẳng $\left( {SBC} \right)$.

A. ${45^ \circ }$.

B. ${30^ \circ }$.

C. ${60^ \circ }$.

D. ${90^ \circ }$.

Lời giải

Chọn B

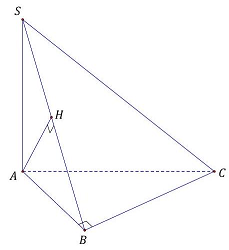
Trong $\left( {SAB} \right)$ kẻ $AH \bot SB\left( {H \in SB} \right)$.

Vì $\left\{ {\begin{array}{*{20}{l}}
{SA \bot BC} \\
{AB \bot BC}
\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH} \right.$.

Mà $SB \bot AH$ do cách dựng nên $AH \bot \left( {SBC} \right)$, hay $H$ là hình chiếu của $A$ lên $\left( {SBC} \right)$ suy ra góc giữa $SA$ và $\left( {SBC} \right)$ là góc $\widehat {ASH}$ hay góc $\widehat {ASB}$.

Tam giác $ABC$ vuông ở $B \Rightarrow AB = \sqrt {A{C^2} – B{C^2}} = a\sqrt 3 $

Tam giác $SAB$ vuông ở $A \Rightarrow sin\widehat {ASB} = \frac{{AB}}{{SB}} = \frac{1}{2} \Rightarrow \widehat {ASB} = {30^ \circ }$

Câu 21: Cho hình lăng trụ đứng $ABC \cdot A’B’C’$ có đáy $ABC$ là tam giác vuông cân tại $A,AB = AA’ = a$ (tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng $BC’$ và mặt phẳng $\left( {ABB’A’} \right)$.

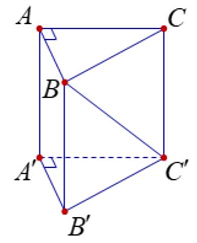
A. $\frac{{\sqrt 2 }}{2}$.

B. $\frac{{\sqrt 6 }}{3}$.

C. $\sqrt 2 $.

D. $\frac{{\sqrt 3 }}{3}$.

Lời giải

$\vartriangle ABC$ vuông cân tại $A \Rightarrow AB = AC = a$.

$\vartriangle ABA’$ vuông tại $A \Rightarrow A’B = a\sqrt 2 $.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{C’A’ \bot A’B’} \\
{C’A’ \bot AA’}
\end{array} \Rightarrow C’A’ \bot \left( {ABB’A’} \right)} \right.$.

$ \Rightarrow BA’$ là hình chiếu của $BC’$ lên mặt phẳng $\left( {ABB’A’} \right)$.

$ \Rightarrow \left( {BC’;\left( {ABB’A’} \right)} \right) = \left( {BC’;BA’} \right)$.

$\Delta A’BC’$ vuông tại $A’ \Rightarrow tan\widehat {A’BC’} = \frac{{A’C’}}{{A’B}} = \frac{a}{{a\sqrt 2 }} = \frac{{\sqrt 2 }}{2}$.

Câu 22: Cho hình lăng trụ đứng $ABC \cdot A’B’C’$ có đáy $ABC$ là tam giác vuông tại $B,AC = 2,BC = 1$, $AA’ = 1$. Tính góc giữa $AB’$ và $\left( {BCC’B’} \right)$.

A. ${45^ \circ }$.

B. ${90^ \circ }$.

C. ${30^ \circ }$.

D. ${60^ \circ }$.

Lời giải

Chọn D

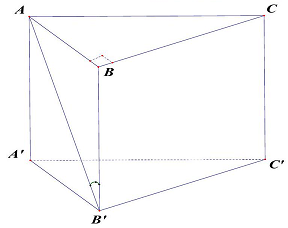
Ta có:
$\left. {\begin{array}{*{20}{c}}
{AB \bot BC} \\
{AB \bot BB’}
\end{array}} \right\} \Rightarrow AB \bot \left( {{\text{BC}}{{\text{C}}^{\text{‘}}}{\text{B’}}} \right)$
, suy ra $BB’$ là hình chiếu vuông góc của $AB’$ trên mặt phẳng $\left( {BCC’B’} \right)$.

Vậy góc giữa đường $AB’$ và $\left( {BCC’B’} \right)$ chính là góc góc $\widehat {AB’B}$.

Xét tam giác $ABB’$ vuông tại $B$ có $BB’ = AA’ = 1,AB = \sqrt {A{C^2} – B{C^2}} = \sqrt 3 $

Suy ra $tan\widehat {AB’B} = \frac{{AB}}{{BB’}} = \sqrt 3 \Rightarrow \widehat {AB’B} = {60^ \circ }$.

Câu 23: Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $2a,\widehat {ABC} = {60^ \circ },SA = a\sqrt 3 $ và $SA \bot \left( {ABCD} \right)$. Tính góc giữa $SA$ và mặt phẳng $\left( {SBD} \right)$.

A. ${60^ \circ }$.

B. ${90^ \circ }$.

C. ${30^ \circ }$.

D. ${45^ \circ }$.

Lời giải

Chọn C

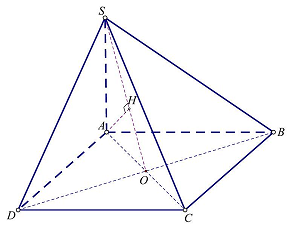
Gọi $O$ là tâm của hình thoi $ABCD$, gọi $H$ là hình chiếu vuông góc của $A$ lên $SO$, ta có: $\left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AH} \right.$.

Từ $AH \bot SO,AH \bot BD$ suy ra $AH \bot \left( {SBD} \right)$, hay $SH$ là hình chiếu vuông góc của $SA$ lên $\left( {SBD} \right)$,

Suy ra $\widehat {\left( {SA,\left( {SBD} \right)} \right)} = \widehat {\left( {SA,SO} \right)} = \widehat {ASO}$.

Ta có $\vartriangle ABC$ đều cạnh $2a$ nên $OA = a$.

$\vartriangle SAO$ vuông tại $A$ nên $tan\widehat {ASO} = \frac{{OA}}{{SA}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {AOS} = {30^ \circ }$.

Câu 24: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. $AB = a,AD = a\sqrt 3 $. Cạnh bên $SA \bot \left( {ABCD} \right)$ và $SA = a\sqrt 2 $. Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là

A. ${30^ \circ }$.

B. ${90^ \circ }$.

C. ${45^ \circ }$.

D. ${60^ \circ }$.

Lời giải

Chọn C

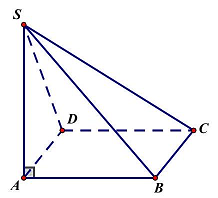
Ta có $BC \bot AB,BC \bot SA \Rightarrow BC \bot \left( {SAB} \right)$.

Hình chiếu vuông góc của $SC$ lên mặt phẳng $\left( {SAB} \right)$ là $SB$.

Suy ra góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là góc $\widehat {BSC}$.

Xét tam giác $\vartriangle SBC$ vuông tại $B$ có $SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 $.

$BC = AD = a\sqrt 3 $.

Suy ra tam giác $\vartriangle SBC$ vuông cân tại $B$.

Suy ra $\widehat {BSC} = {45^ \circ }$.

Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng ${45^ \circ }$.

Câu 25: Cho hình chóp tứ giác $S.ABCD$ có đáy là hình vuông cạnh $a,SA \bot \left( {ABCD} \right)$ và $SA = a$. Góc giữa đường thẳng $SB$ và $\left( {SAC} \right)$ là

A. ${30^ \circ }$.

B. ${75^ \circ }$.

C. ${60^ \circ }$.

D. ${45^ \circ }$.

Lời giải.

Chọn A

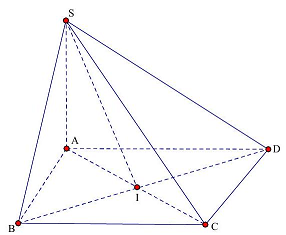
Gọi $I$ là tâm của hình vuông $ABCD$.

Vì $ABCD$ là hình vuông nên $BD \bot AC$; Vì $SA \bot \left( {ABCD} \right)$ nên $SA \bot BD$

Suy ra $BD \bot \left( {SAC} \right)$, do đó góc giữa đường thẳng $SB$ và $\left( {SAC} \right)$ là góc $\widehat {BSI}$

Ta có: $SB = a\sqrt 2 ;BI = \frac{{a\sqrt 2 }}{2} \Rightarrow sin\widehat {BSI} = \frac{{BI}}{{SB}} = \frac{1}{2} \Rightarrow \widehat {BSI} = {30^ \circ }$.

Câu 26: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$ cùng vuông góc với đáy $\left( {ABCD} \right)$ và $SA = 2a$. Tính cosin của góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAD} \right)$.

A. $\frac{{\sqrt 5 }}{5}$.

B. $\frac{{2\sqrt 5 }}{5}$.

C. $\frac{1}{2}$.

D. 1 .

Lời giải

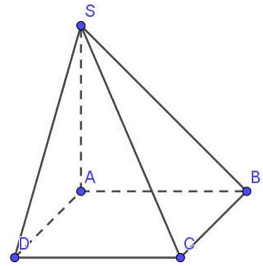
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{\left( {SAB} \right) \bot \left( {ABCD} \right)} \\
{\left( {SAC} \right) \bot \left( {ABCD} \right)\; \Rightarrow SA \bot \left( {ABCD} \right).\;} \\
{\left( {SAB} \right) \cap \left( {SAC} \right) = SA}
\end{array}} \right.$

mà $\left\{ \begin{gathered}
AB \bot AD \hfill \\
AB \bot SA \hfill \\
AD \cap SA = A \hfill \\
\end{gathered} \right.$ $ \Rightarrow AB \bot (SAD)$

$cos\widehat {\left( {SB,\left( {SAD} \right)} \right)} = cos\widehat {BSA} = \frac{{SA}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{2}{{\sqrt 5 }}$

Câu 27: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a\sqrt 2 ,AD = a,SA$ vuông góc với đáy và $SA = a$. Tính góc giữa $SC$ và $\left( {SAB} \right)$.

A. ${90^ \circ }$.

B. ${60^ \circ }$.

C. ${45^ \circ }$.

D. ${30^ \circ }$.

Lời giải

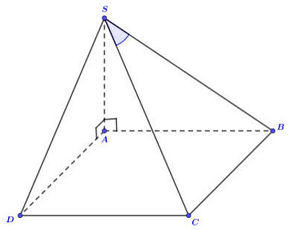
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow SA \bot \left( {SAB} \right) \Rightarrow SB} \right.$ là hình chiếu vuông góc của $SC$ lên $\left( {SAB} \right)$

$ \Rightarrow \widehat {\left( {SC,\left( {SAB} \right)} \right)} = \widehat {CSB}$.

Tam giác $SAB$ vuông tại $A$ có: $SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 3 $.

Tam giác $SBC$ vuông tại $B$ có: $tan\widehat {CSB} = \frac{{BC}}{{SB}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {CSB} = {30^ \circ }$.

Câu 28: Cho hình lập phương $ABCD \cdot A’B’C’D’$ (hình bên). Tính góc giữa đường thẳng $AB’$ và mặt phẳng $\left( {BDD’B’} \right)$.

A. ${60^ \circ }$.

B. ${90^ \circ }$.

C. ${45^ \circ }$.

D. ${30^ \circ }$.

Lời giải

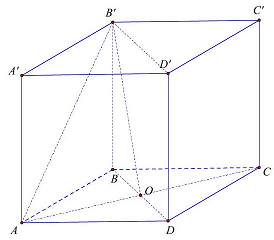
Gọi $O$ là tâm của hình vuông $ABCD$ khi đó ta có $AO \bot BD$ (1).

Mặt khác ta lại có $ABCD \cdot A’B’C’D’$ là hình lập phương nên $BB’ \bot \left( {ABCD} \right) \Rightarrow BB’ \bot AO$ (2).

Từ (1) và (2) ta có $AO \bot \left( {BDD’B’} \right) \Rightarrow \left( {AB’,\left( {ABCD} \right)} \right) = \left( {AB’,B’O} \right) = \widehat {AB’O}$.

Xét tam giác vuông $AB’O$ có $sinAB’O = \frac{{AO}}{{AB’}} = \frac{1}{2} \Rightarrow \widehat {AB’O} = {30^ \circ }$.

Vậy $\left( {AB’,\left( {ABCD} \right)} \right) = {30^ \circ }$.

Câu 29: Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình chữ nhật có $AB = 2AD = 2a$ cạnh bên $SA$ vuông góc với đáy và $SA = a\sqrt {15} $. Tính tang của góc giữa $SC$ và mặt phẳng $\left( {SAD} \right)$.

A. $\sqrt 3 $.

B. 2 .

C. $\frac{1}{2}$.

D. $\frac{{\sqrt 3 }}{3}$.

Lời giải

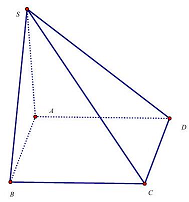
Ta có $\left. {\begin{array}{*{20}{c}}
{CD \bot AD} \\
{CD \bot SA}
\end{array}} \right\} \Rightarrow CD \bot \left( {SAD} \right)$. Do đó góc giữa $SC$ và mặt phẳng $\left( {SAD} \right)$ là góc $\widehat {CSD}$.

$tan\widehat {CSD} = \frac{{CD}}{{SD}} = \frac{{CD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{2a}}{{\sqrt {15{a^2} + {a^2}} }} = \frac{1}{2}$.

Câu 30: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $I$, cạnh $a$, góc $\widehat {BAD} = {60^ \circ }$. $SA = SB = SD = \frac{{a\sqrt 3 }}{2}$. Gọi $\alpha $ là góc giữa đường thẳng $SD$ và mặt phẳng $\left( {SBC} \right)$. Giá trị $sin\alpha $ bằng

A. $\frac{1}{3}$.

B. $\frac{2}{3}$.

C. $\frac{{\sqrt 5 }}{3}$.

D. $\frac{{2\sqrt 2 }}{3}$.

Lời giải

Chọn C

Theo giả thiết, $ABD$ là tam giác đều.

Gọi $H$ là tâm đường tròn ngoại tiếp tam giác $ABD$. Do $SA = SB = SD$ nên $S$ nằm trên trục của đường tròn ngoại tiếp tam giác $ABD$ suy ra $SH \bot \left( {ABD} \right)$ hay $SH \bot \left( {ABCD} \right)$.

Do $\left( {SBC} \right) \bot \left( {SBH} \right)$ nên từ $H$ kẻ $HK \bot SB$ tại $K$ thì $HK = d\left( {H,\left( {SBC} \right)} \right)$ và

$\frac{1}{{H{K^2}}} = \frac{1}{{H{B^2}}} + \frac{1}{{H{S^2}}} \Rightarrow HK = \frac{{a\sqrt {15} }}{9}$.

Mặt khác, $d\left( {H,\left( {SBC} \right)} \right) = \frac{2}{3}d\left( {A,\left( {SBC} \right)} \right) = \frac{2}{3}d\left( {D,\left( {SBC} \right)} \right) \Rightarrow d\left( {D,\left( {SBC} \right)} \right) = \frac{{a\sqrt {15} }}{6}$.

Gọi $O$ là hình chiếu vuông góc của điểm $D$ trên $\left( {SBC} \right)$. Khi đó: $\alpha = \left( {SD,SO} \right) = \widehat {DSO}$ và $DO = d\left( {D,\left( {SBC} \right)} \right) = \frac{{a\sqrt {15} }}{6}$.

Xét tam giác $SDO$ vuông tại $O$ có: $sin\alpha = \frac{{DO}}{{SD}} = \frac{{\frac{{a\sqrt {15} }}{6}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 5 }}{3}$.

Câu 31: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,SA$ vuông góc với đáy và $SA = a\sqrt 3 $. Gọi $\alpha $ là góc giữa $SD$ và $\left( {SAC} \right)$. Giá trị $sin\alpha $ bằng

A. $\frac{{\sqrt 2 }}{4}$.

B. $\frac{{\sqrt 2 }}{2}$.

C. $\frac{{\sqrt 3 }}{2}$.

D. $\frac{{\sqrt 2 }}{3}$.

Lời giải

Chọn A

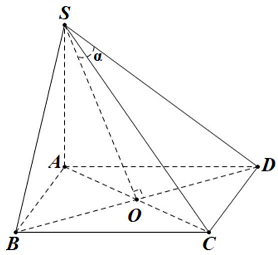
Gọi $O = AC \cap BD$. Ta có: $\left\{ {\begin{array}{*{20}{l}}
{DO \bot AC} \\
{DO \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)}
\end{array} \Rightarrow DO \bot \left( {ABCD} \right)} \right.$.

$ \Rightarrow SO$ là hình chiếu của $SD$ lên mặt phẳng $\left( {SAC} \right) \Rightarrow \widehat {\left( {SD;\left( {SAC} \right)} \right)} = \widehat {\left( {SD;SO} \right)} = \widehat {DSO} = \alpha $.

Xét $\vartriangle SAD$ vuông tại $A:SD = \sqrt {3{a^2} + {a^2}} = 2a$.

Xét $\vartriangle SOD$ vuông tại $O$ : có $SD = 2a,OD = \frac{{a\sqrt 2 }}{2} \Rightarrow sin\alpha = sin\widehat {DSO} = \frac{{DO}}{{SD}} = \frac{{\sqrt 2 }}{4}$.

Câu 32: Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $a$, góc $\widehat {ABC} = {60^ \circ },SA \bot \left( {ABCD} \right),SA = a\sqrt 3 $. Gọi $\alpha $ là góc giữa $SA$ và mặt phẳng $\left( {SCD} \right)$. Tính $tan\alpha $.

A. $\frac{1}{2}$.

B. $\frac{1}{3}$.

C. $\frac{1}{4}$.

D. $\frac{1}{5}$.

Lời giải

Chọn A

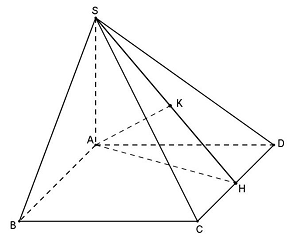
Trong mặt phẳng $\left( {ABCD} \right)$ kẻ $AH \bot CD$ tại $H$.

Trong mặt phẳng $\left( {SAH} \right)$ kẻ $AK \bot SH$ tại $K$. Khi đó $AK \bot \left( {SCD} \right)$ nên góc giữa $SA$ mặt phẳng $\left( {SCD} \right)$ là $\widehat {ASH} = \alpha $.

Tam giác $ADC$ đều nên $AH = \frac{{a\sqrt 3 }}{2}$.

Trong tam giác vuông $ASH$ có $tan\widehat {ASH} = \frac{{AH}}{{AS}} = \frac{1}{2}$.

Câu 33: Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, cạnh bên $SA$ vuông góc với mặt phẳng đáy, $AB = 2a,\widehat {BAC} = {60^ \circ }$ và $SA = a\sqrt 2 $. Góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$ bằng

A. ${30^ \circ }$.

B. ${45^0}$.

C. ${60^ \circ }$.

D. ${90^ \circ }$.

Lời giải

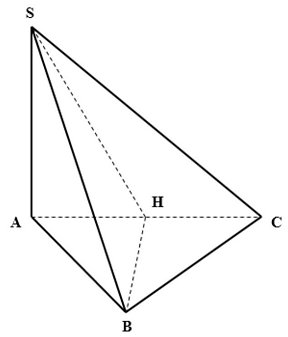
Trong mặt phẳng $\left( {ABC} \right)$ kẻ $BH \bot AC$

Mà $BH \bot SA \Rightarrow BH \bot \left( {SAC} \right)$

Góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$ bằng $\widehat {BSH}$.

Xét tam giác $ABH$ vuông tại $H,BH = AB \cdot sin{60^ \circ } = 2a \cdot \frac{{\sqrt 3 }}{2} = a\sqrt 3 $

$AH = AB \cdot cos{60^ \circ } = 2a \cdot \frac{1}{2} = a$.

Xét tam giác $SAH$ vuông tại $S,SH = \sqrt {S{A^2} + A{H^2}} = \sqrt {{{(a\sqrt 2 )}^2} + {a^2}} = a\sqrt 3 $.

Xét tam giác $SBH$ vuông tại $H$ có $SH = HB = a\sqrt 3 $ suy ra tam giác $SBH$ vuông tại $H$.

Vậy $\widehat {BSH} = {45^ \circ }$.

Câu 34: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành, $AB = 2a,BC = a,\widehat {ABC} = {120^ \circ }$. Cạnh bên $SD = a\sqrt 3 $ và $SD$ vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên). Tính $sin$ của góc tạo bởi $SB$ và mặt phẳng $\left( {SAC} \right)$

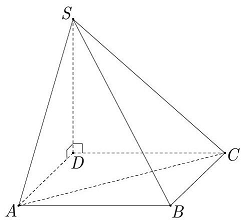
A. $\frac{3}{4}$.

B. $\frac{{\sqrt 3 }}{4}$.

C. $\frac{1}{4}$.

D. $\frac{{\sqrt 3 }}{7}$.

Lời giải

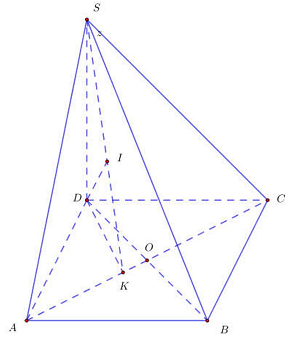
Ta có $sin\left( {\widehat {SB;\left( {SAC} \right))} = \frac{{d\left( {B;\left( {SAC} \right)} \right)}}{{SB}} = \frac{{d\left( {D;SAC} \right)}}{{SB}}} \right.$.

Xét tam giác $ABC$ ta có $AC = \sqrt {B{A^2} + B{C^2} – 2BA \cdot BC \cdot cos\widehat {BAC}} = a\sqrt 7 $.

$BO = \sqrt {\frac{{B{A^2} + B{C^2}}}{2} – \frac{{A{C^2}}}{4}} = \sqrt {\frac{{4{a^2} + {a^2}}}{2} – \frac{{7{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}$

$ \Rightarrow BD = a\sqrt 3 $ và $SB = \sqrt {S{D^2} + B{D^2}} = \sqrt {3{a^2} + 3{a^2}} = a\sqrt 6 $.

Xét tam giác $ADC$ ta có $\frac{{AD}}{{sin\hat C}} = \frac{{AC}}{{sin\hat D}} \Rightarrow sin\hat C = \frac{{AD \cdot sin\hat D}}{{AC}} = \frac{{a \cdot sin{{120}^ \circ }}}{{a\sqrt 7 }} = \frac{{\sqrt {21} }}{{14}}$.

Gọi $K$ là hình chiếu của $D$ lên $AC$, và $I$ là hình chiếu của $D$ lên $SK$. Ta có $\left\{ {\begin{array}{*{20}{l}}
{AC \bot DK} \\
{AC \bot SD}
\end{array} \Rightarrow AC \bot DI} \right.$. Do đó $\left\{ {\begin{array}{*{20}{l}}
{DI \bot SK} \\
{DI \bot AC}
\end{array} \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = DI} \right.$.

Mặt khác $sin\hat C = \frac{{DK}}{{DC}} \Rightarrow DK = DC \cdot sin\hat C = 2a \cdot \frac{{\sqrt {21} }}{{14}} = \frac{{a\sqrt {21} }}{7}$.

Xét tam giác $SDK$ ta có $DI = \frac{{SD \cdot DK}}{{\sqrt {S{D^2} + D{K^2}} }} = \frac{{a\sqrt 3 \cdot \frac{{a\sqrt {21} }}{7}}}{{\sqrt {3{a^2} + \frac{{21}}{{49}}{a^2}} }} = \frac{{\sqrt 6 }}{4}a$.

Vậy $sin\widehat {\left( {SB;\left( {SAC} \right)} \right)} = \frac{{d\left( {D;SAC} \right)}}{{SB}} = \frac{{DI}}{{SB}} = \frac{{\frac{{\sqrt 6 }}{4}a}}{{a\sqrt 6 }} = \frac{1}{4}$.

Trong mặt phẳng $\left( {SDK} \right)$ kẻ $DI \bot SK$ suy ra $d\left( {D;\left( {SAC} \right)} \right) = DI$.

Câu 35: Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh bằng $a$, gọi $\alpha $ là góc giữa đường thẳng $A’B$ và mặt phẳng $\left( {BB’D’D} \right)$. Tính $sin\alpha $.

A. $\frac{{\sqrt 3 }}{4}$.

B. $\frac{{\sqrt 3 }}{2}$.

C. $\frac{{\sqrt 3 }}{5}$.

D. $\frac{1}{2}$.

Lời giải

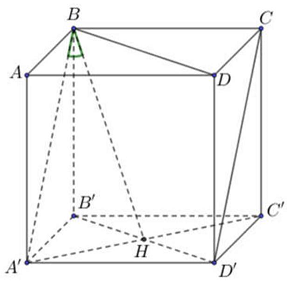
Gọi $H$ là tâm hình vuông $A’B’C’D’$.

Ta có $A’H \bot B’D’,A’H \bot BB’ \Rightarrow A’H \bot \left( {BB’D’D} \right)$. $BH$ là hình chiếu của $A’B$ trên $\left( {BB’D’D} \right)$

$ \Rightarrow \left( {\widehat {A’H,\left( {BB’D’D} \right)}} \right) = \widehat {A’BH} = \alpha \cdot sin\alpha = \frac{{A’H}}{{A’B}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 2 }} = \frac{1}{2}$.

Câu 36: Cho hình chóp $S.ABC$ có đáy là tam giác vuông tại $B$, cạnh bên $SA$ vuông góc với mặt đáy, $AB = 2a,\widehat {BAC} = {60^ \circ }$ và $SA = a\sqrt 2 $. Góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$ bằng

A. ${45^ \circ }$.

B. ${60^ \circ }$.

C. ${30^ \circ }$.

D. ${90^ \circ }$.

Lời giải

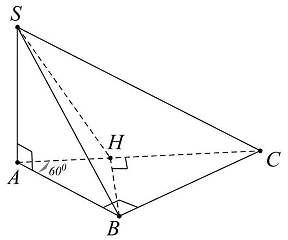
Kẻ $BH \bot AC\left( {H \in AC} \right)$ và theo giả thiết $BH \bot SA$ nên $BH \bot \left( {SAC} \right)$

Do đó, $SH$ là hình chiếu vuông góc của $SB$ lên mặt phẳng $\left( {SAC} \right)$

Suy ra, $\overline {\left( {SB,\left( {SAC} \right)} \right)} = \widehat {\left( {SB,SH} \right)} = \widehat {BSH}$.

Mà ta có: $SB = a\sqrt 6 ,HB = ABsin{60^ \circ } = a\sqrt 3 \Rightarrow sin\left( {\widehat {BSH}} \right) = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {BSH} = {45^ \circ }$.

Câu 37: Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh bằng nhau. Gọi $E,M$ lần lượt là trung điểm của các cạnh $BC$ và $SA,\alpha $ là góc tạo bởi đường thẳng $EM$ và mặt phẳng $\left( {SBD} \right)$. Giá trị của tan $\alpha $ bằng

A. 2 .

B. $\sqrt 3 $.

C. 1 .

D. $\sqrt 2 $.

Lời giải

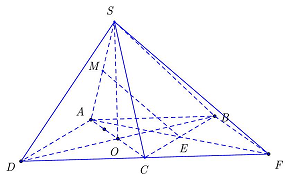
Dựng hình bình hành $ABFC$.

Ta có $EM//SF$ nên góc giữa $EM$ và $\left( {SBD} \right)$ bằng góc giữa $SF$ và $\left( {SBD} \right)$.

$FB//AC \Rightarrow FB \bot \left( {SBD} \right)$ do đó góc giữa $SF$ và $\left( {SBD} \right)$ bằng góc $\widehat {FSB}$.

Ta có $tan\widehat {FSB} = \frac{{BF}}{{SB}} = \frac{{AC}}{{SB}} = \sqrt 2 $.

Vậy chọn D.

Câu 38: Cho hình hộp $ABCD \cdot A’B’C’D’$ có $M,N,P$ lần lượt là trung điểm của các cạnh $A’B’,A’D’$, $C’D’$. Góc giữa đường thẳng $CP$ và mặt phẳng $\left( {DMN} \right)$ bằng?

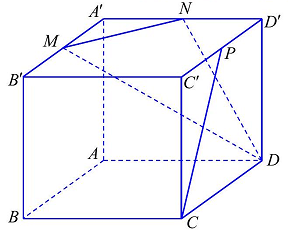
A. ${0^ \circ }$.

B. ${45^ \circ }$.

C. ${30^ \circ }$.

D. ${60^ \circ }$.

Lời giải

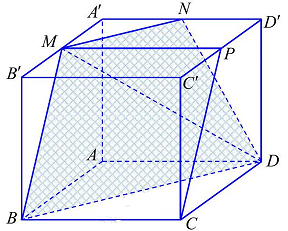
Ta có $\left\{ {\begin{array}{*{20}{l}}
{MN//B’D’} \\
{BD//B’D’}
\end{array} \Rightarrow MN//BD \Rightarrow } \right.$ bốn điểm $M,N,B,D$ đồng phẳng.

Lại có tứ giác $BCPM$ là hình bình hành $ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{CP//BM} \\
{BM \subset \left( {DMN} \right)}
\end{array} \Rightarrow CP//\left( {DMN} \right)} \right.$

$ \Rightarrow \left( {\overline {CP,\left( {DMN} \right)} } \right) = {0^ \circ }$.

Câu 39: Cho tứ diện $ABCD$ có tam giác $BCD$ đều cạnh $a,AB$ vuông góc với $mp\left( {BCD} \right),AB = 2a.M$ là trung điểm đoạn $AD$, gọi $\varphi $ là góc giữa $CM$ với $mp\left( {BCD} \right)$,khi đó:

A. $tan\varphi = \frac{{\sqrt 3 }}{2}$.

B. $tan\varphi = \frac{{2\sqrt 3 }}{3}$.

C. $tan\varphi = \frac{{3\sqrt 2 }}{2}$.

D. $tan\varphi = \frac{{\sqrt 6 }}{3}$.

Lời giải

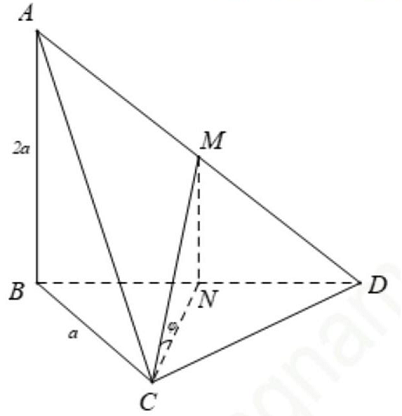
Gọi $N$ là trung điểm $BC$. Ta có góc giữa $CM$ với $mp\left( {BCD} \right)$ bằng góc $MCN$.

$ + MN = \frac{{AB}}{2} = a$.

$ + CN = \frac{{a\sqrt 3 }}{2}$.

Vậy $tan\varphi = \frac{{MN}}{{CN}} = a \cdot \frac{2}{{a\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}$.

Câu 40: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $2a$. Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $M,N$ lần lượt là trung điểm của $SC$ và $AD$ (tham khảo hình vẽ).

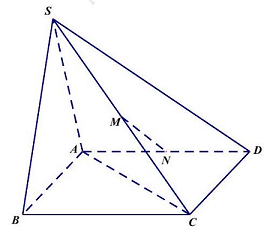
Góc giữa $MN$ và mặt đáy $\left( {ABCD} \right)$ bằng

A. ${90^ \circ }$.

B. ${30^ \circ }$.

C. ${45^ \circ }$.

D. ${60^ \circ }$.

Lời giải

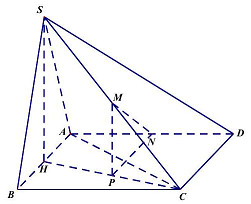
Gọi $H$ là trung điểm $AB \Rightarrow SH \bot \left( {ABCD} \right)$ và $SH = \frac{{a\sqrt 3 }}{2}$.

Gọi $P$ là trung điểm $CH \Rightarrow MP//SH \Rightarrow MP \bot \left( {ABCD} \right)$, suy ra góc giữa $MN$ với mặt đáy $\left( {ABCD} \right)$ là góc $\widehat {MNP}$ (do $\widehat {MPN} = {90^ \circ }$ )

Có $MP = \frac{1}{2}SH = \frac{{a\sqrt 3 }}{4},PN = \frac{{AH + CD}}{2} = \frac{{\frac{a}{2} + a}}{2} = \frac{{3a}}{4}$

$ \Rightarrow tan\widehat {MNP} = \frac{{MP}}{{PN}} = \frac{{\frac{{a\sqrt 3 }}{4}}}{{\frac{{3a}}{4}}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {MNP} = {30^ \circ }$.

Câu 41: Cho tứ diện đều $ABCD$ có cạnh bằng $a$. Gọi $M,N$ lần lượt là trung điểm của $BC$ và $AD$ (tham khảo hình vẽ). Gọi $\varphi $ là góc giữa đường thẳng $MN$ và mặt phẳng $\left( {BCD} \right)$. Tính $tan\varphi $.

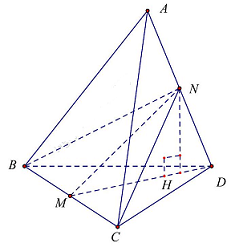
A. $tan\varphi = \sqrt 2 $.

B. $tan\varphi = \frac{{\sqrt 2 }}{2}$.

C. $tan\varphi = \sqrt 3 $.

D. $tan\varphi = \frac{{\sqrt 3 }}{3}$.

Lời giải

Trong $\vartriangle AMD$, kẻ $NH \bot MD$, suy ra $NH \bot \left( {BCD} \right)$.

Nên $MD$ là hình chiếu vuông góc của $MN$ lên mặt phẳng $BCD$.

Khi đó $\left( {\widehat {MN,\left( {BCD} \right)}} \right) = \left( {\widehat {MN,MD}} \right) = \widehat {NMD}$.

Ta có $\vartriangle NMD$ vuông tại $N$ do đó $tan\varphi = \frac{{ND}}{{MN}} = \frac{{\frac{a}{2}}}{{a\frac{{\sqrt 2 }}{2}}} = \sqrt 2 $.

Câu 42: Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right),SA = 2a\sqrt 3 ,AB = 2a$, tam giác $ABC$ vuông cân tại $B$. Gọi $M$ là trung điểm của $SB$. Góc giữa đường thẳng $CM$ và mặt phẳng $\left( {SAB} \right)$ bằng:

A. ${90^ \circ }$.

B. ${60^ \circ }$.

C. ${45^ \circ }$.

D. ${30^ \circ }$.

Chọn C

Lời giải

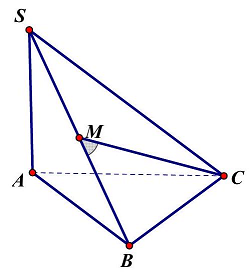
Có $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.$

Có $BM$ là hình chiếu của $CM$ lên mặt phẳng $\left( {SAB} \right)$. Suy ra $\left( {CM;\left( {SAB} \right)} \right) = \widehat {CMB}$

Ta có $tan\widehat {CMB} = \frac{{BC}}{{MB}} = \frac{{2AB}}{{SB}} = \frac{{2AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{2.2a}}{{\sqrt {{{(2a\sqrt 3 )}^2} + {{(2a)}^2}} }} = 1$

$ \Rightarrow \widehat {CMB} = {45^ \circ }$

Vậy $\left( {CM;\left( {SAB} \right)} \right) = {45^ \circ }$

Câu 43: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Tam giác $SAB$ đều và nàm trong mặt phẳng vuông góc với đáy. Gọi $H,K$ lần lượt là trung điểm của các cạnh $AB$ và $AD$. Tính sin của góc tạo bởi giữa hai đường thẳng $SA$ và mặt phẳng $\left( {SHK} \right)$.

A. $\frac{{\sqrt 2 }}{2}$.

B. $\frac{{\sqrt 2 }}{4}$.

C. $\frac{{\sqrt {14} }}{4}$.

D. $\frac{{\sqrt 7 }}{4}$.

Lời giải

Chọn B

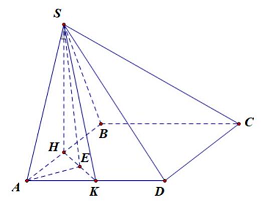
Gọi $E$ là trung điểm của đoạn $KH$, ta có $\vartriangle AHK$ vuông cân tại $A$ vì $AH = AK = \frac{1}{2}a$ nên $AE \bot KH$ do đó

$\left\{ {\begin{array}{*{20}{l}}
{AE \bot SH} \\
{AE \bot HK}
\end{array} \Rightarrow AE \bot \left( {SHK} \right)} \right.$, suy ra

$\widehat {\left( {SA,\left( {SHK} \right)} \right)} = \widehat {\left( {SA,SE} \right)} = \widehat {ASE} = \alpha $

Mà $AE = \frac{1}{2}KH = \frac{1}{2}\sqrt {A{H^2} + A{K^2}} = \frac{{a\sqrt 2 }}{4}$.

$\vartriangle SEA$ vuông tại $E$ có $sin\alpha = \frac{{AE}}{{SA}} = \frac{{\sqrt 2 }}{4}$.

Vậy $sin\alpha = \frac{{\sqrt 2 }}{4}$.

Câu 44: Cho hình chóp tứ giác đều $S \cdot ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm của $SD$ (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng $BM$ và mặt phẳng $\left( {ABCD} \right)$ bằng

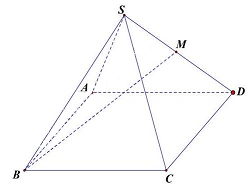
A. $\frac{{\sqrt 2 }}{2}$.

B. $\frac{{\sqrt 3 }}{3}$.

C. $\frac{2}{3}$.

D. $\frac{1}{3}$.

Lời giải

Chọn D

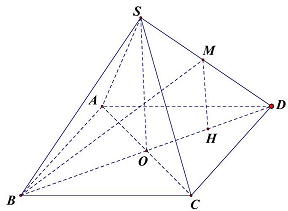
Gọi $O$ là tâm của hình vuông. Ta có $SO \bot \left( {ABCD} \right)$ và $SO = \sqrt {{a^2} – \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2}$

Gọi $M$ là trung điểm của $OD$ ta có $MH//SO$ nên $H$ là hình chiếu của $M$ lên mặt phẳng $\left( {ABCD} \right)$ và $MH = \frac{1}{2}SO = \frac{{a\sqrt 2 }}{4}$.

Do đó góc giữa đường thẳng $BM$ và mặt phẳng $\left( {ABCD} \right)$ là $\widehat {MBH}$.

Khi đó ta có $tan\widehat {MBH} = \frac{{MH}}{{BH}} = \frac{{\frac{{a\sqrt 2 }}{4}}}{{\frac{{3a\sqrt 2 }}{4}}} = \frac{1}{3}$.

Vậy tang của góc giữa đường thẳng $BM$ và mặt phẳng $\left( {ABCD} \right)$ bằng $\frac{1}{3}$.

Câu 45: Cho hình chóp đều $S.ABCD$ có $SA = \sqrt 5 a,AB = a$. Gọi $M,N,P,Q$ lần lượt là trung điểm của $SA,SB,SC,SD$. Tính cosin của góc giữa đường thẳng $DN$ và mặt phẳng $\left( {MQP} \right)$.

A. $\frac{{\sqrt 2 }}{2}$.

B. $\frac{1}{2}$.

C. $\frac{{\sqrt 3 }}{2}$.

D. $\frac{{\sqrt {15} }}{6}$.

Lời giải

Chọn A

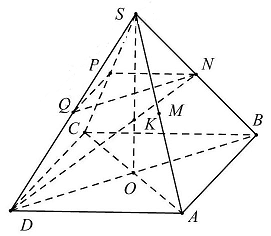
Do $M,N,P,Q$ lần lượt là trung điểm của $SA,SB,SC,SD$ nên mặt phẳng $\left( {ABCD} \right)$ song song mặt phẳng $\left( {MPQ} \right)$ suy ra góc giữa đường thẳng $DN$ và mặt phẳng $\left( {MQP} \right)$ cũng là góc giữa đường thẳng $DN$ và mặt phẳng $\left( {ABCD} \right)$.

Có $K = SO \cap DN$. Do $S.ABCD$ hình chóp đều nên $SO \bot \left( {ABCD} \right)$ suy ra hình chiếu vuông góc của đường thẳng $DN$ trên mặt phẳng $\left( {ABCD} \right)$ là đường thẳng $DO$ nên

$\overline {\left( {DN,\left( {ABCD} \right)} \right)} = \overline {\left( {DN,DO} \right)} $.

Xét tam giác vuông $SOA$ có $OA = \frac{{\sqrt 2 }}{2}a;SA = \sqrt 5 a \Rightarrow SO = \frac{{3\sqrt 2 }}{2}a$. Mà $K$ là trọng tâm tam giác $SBD \Rightarrow OK = \frac{1}{3}SO = \frac{{\sqrt 2 a}}{2} = OD \Rightarrow \vartriangle OKD$ vuông cân tại $O$ hay $\widehat {KDO} = {45^ \circ }$.

Hay $\overline {\left( {DN,\left( {MPQ} \right)} \right)} = {45^ \circ } \Rightarrow cos\left( {\overline {DN,\left( {MPQ} \right))} = \frac{{\sqrt 2 }}{2}} \right.$.

Câu 46: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a,BC = a\sqrt 3 ,SA = a$ và $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Đặt $\alpha $ là góc giữa đường thẳng $BD$ và $\left( {SBC} \right)$. Giá trị của $sin\alpha $ bằng

A. $\frac{{\sqrt 2 }}{4}$.

B. $\frac{{\sqrt 5 }}{5}$.

C. $\frac{1}{2}$.

D. $\frac{{\sqrt 3 }}{2}$.

Lời giải

Chọn A

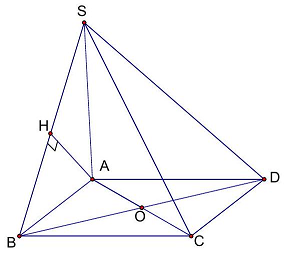
Ta có $sin\alpha = \frac{{d\left( {D,\left( {SBC} \right)} \right)}}{{BD}} = \frac{{d\left( {A,\left( {SBC} \right)} \right)}}{{BD}}$.

$\left\{ {\begin{array}{*{20}{l}}
{\left( {SAB} \right) \bot \left( {SBC} \right)} \\
{\left( {SAB} \right) \cap \left( {SBC} \right) = SB}
\end{array}} \right.$. Kẻ $AH \bot SB$ thì $AH \bot \left( {SBC} \right) \Rightarrow AH = d\left( {A,\left( {SBC} \right)} \right)$.

$\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{S^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2}}} = \frac{2}{{{a^2}}} \Rightarrow AH = \frac{{a\sqrt 2 }}{2}$ và $BD = \sqrt {B{A^2} + A{D^2}} = 2a$.

Vậy $sin\alpha = \frac{{d\left( {A,\left( {SBC} \right)} \right)}}{{BD}} = \frac{{AH}}{{BD}} = \frac{{a\sqrt 2 }}{{2 \cdot 2a}} = \frac{{\sqrt 2 }}{4}$.

Câu 47: Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh bằng nhau. Gọi $M,N$ lần lượt là trung điểm của các cạnh $BC,SA$ và $\alpha $ là góc tạo bởi đường thẳng $MN$ với $\left( {SBD} \right)$. Tính $tan\alpha $.

A. $\sqrt 3 $.

B. 1 .

C. 2 .

D. $\sqrt 2 $.

Lời giải

Chọn D

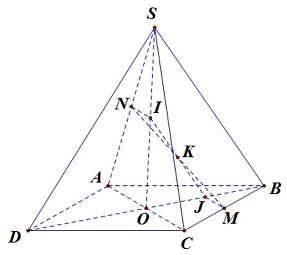
Gọi $O = AC \cap BD,I,J$ lần lượt là trung điểm của $OS,OB$.

Ta có $\left. {\begin{array}{*{20}{l}}
{OA \bot \left( {SBD} \right)} \\
{NI//AC//MJ}
\end{array}} \right\} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{NI \bot \left( {SBD} \right)} \\
{MJ \bot \left( {SBD} \right)}
\end{array}} \right.$.

Suy ra $\left( {MN,\left( {SBD} \right)} \right) = \left( {MN,IJ} \right)$

Có: $\left. {\begin{array}{*{20}{c}}
{NI//AC//MJ} \\
{NI = \frac{1}{4}AC = MJ}
\end{array}} \right\} \Rightarrow MJNI$ là hình bình hành. Gọi $K = MN \cap IJ$ suy ra $K$ là trung điểm của $IJ$ và $MN$ đồng thời $NI \bot IK$

Ta có $tan\alpha = tan\widehat {NKI} = \frac{{NI}}{{IK}} = \frac{{OA}}{{SB}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{a}{2}}} = \sqrt 2 $ trong đó $a$ là cạnh của hình vuông $ABCD$.

Câu 48: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, tâm $O$. Gọi $M$ và $N$ lần lượt là trung điểm của $SA$ và $BC$. Biết rằng góc giữa $MN$ và $\left( {ABCD} \right)$ bằng ${60^ \circ }$, cosin góc giữa $MN$ và mặt phẳng $\left( {SBD} \right)$ bằng:

A. $\frac{{\sqrt {41} }}{{41}}$.

B. $\frac{{\sqrt 5 }}{5}$.

C. $\frac{{2\sqrt 5 }}{5}$.

D. $\frac{{2\sqrt {41} }}{{41}}$.

Lời giải

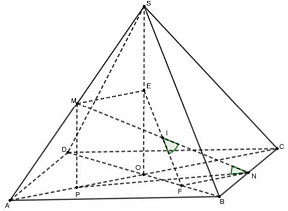
Gọi $E,F$ lần lượt là trung điểm $SO,OB$ thì $EF$ là hình chiếu của $MN$ trên $\left( {SBD} \right)$.

Gọi $P$ là trung điểm $OA$ thì $PN$ là hình chiếu của $MN$ trên $\left( {ABCD} \right)$.

Theo bài ra: $\widehat {MNP} = {60^ \circ }$.

Áp dụng định lý cos trong tam giác $CNP$ ta được:

$N{P^2} = C{P^2} + C{N^2} – 2CP \cdot CN \cdot cos{45^ \circ } = {\left( {\frac{{3a\sqrt 2 }}{4}} \right)^2} + \frac{{{a^2}}}{4} – 2 \cdot \frac{{3a\sqrt 2 }}{4} \cdot \frac{a}{2} \cdot \frac{{\sqrt 2 }}{2} = \frac{{5{a^2}}}{8}$.

Suy ra: $NP = \frac{{a\sqrt {10} }}{4},MP = NP \cdot tan{60^ \circ } = \frac{{a\sqrt {30} }}{4};SO = 2MP = \frac{{a\sqrt {30} }}{2}$.

$SB = \sqrt {S{O^2} + O{B^2}} = 2a\sqrt 2 \Rightarrow EF = a\sqrt 2 $.

Ta lại có: $MENF$ là hình bình hành ( vì $ME$ và $NF$ song song và cùng bằng $\frac{1}{2}OA$ ).

Gọi $I$ là giao điểm của $MN$ và $EF$, khi đó góc giữa $MN$ và mặt phẳng $\left( {SBD} \right)$ là $\widehat {NIF}$.

$cos\widehat {NIF} = \frac{{IK}}{{IN}} = \frac{{a\sqrt 2 }}{2} \cdot \frac{4}{{a\sqrt {10} }} = \frac{{2\sqrt 5 }}{5}$.

Câu 49: Cho lăng trụ $ABC \cdot A’B’C’$ có đáy là tam giác đều cạnh $a$. Hình chiếu vuông góc của $B’$ lên mặt phẳng $\left( {ABC} \right)$ trùng với trọng tâm $G$ của tam giác $ABC$. Cạnh bên hợp với $\left( {ABC} \right)$ góc ${60^ \circ }$. Sin của góc giữa $AB$ và mặt phẳng $\left( {BCC’B’} \right)$.

A. $\frac{3}{{\sqrt {13} }}$.

B. $\frac{3}{{2\sqrt {13} }}$.

C. $\frac{1}{{\sqrt {13} }}$.

D. $\frac{2}{{\sqrt {13} }}$.

Lời giải

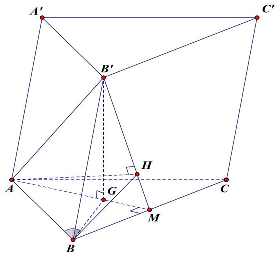
Ta có $B’G \bot \left( {ABC} \right)$ nên $BG$ là hình chiếu của $BB’$ lên mặt phẳng $\left( {ABC} \right)$.

$ \Rightarrow \left( {BB’,\left( {ABC} \right)} \right) = \left( {BB’,BG} \right) = \widehat {B’BG} = {60^ \circ }$.

Gọi $M$ là trung điểm $BC$ và $H$ là hình chiếu của $A$ lên $B’M$, ta có

$\left\{ {\begin{array}{*{20}{l}}
{BC \bot AM} \\
{BC \bot B’G}
\end{array} \Rightarrow BC \bot \left( {AB’M} \right) \Rightarrow BC \bot AH} \right.$.

Mà $AH \bot B’M$ nên $AH \bot \left( {BCC’B’} \right)$.

Do đó $HB$ là hình chiếu của $AB$ lên mặt phẳng $\left( {BCC’B’} \right)$.

$ \Rightarrow \left( {AB,\left( {BCC’B’} \right)} \right) = \left( {AB,HB} \right) = \widehat {ABH}$.

Xét tam giác $ABH$ vuông tại $H$ có $sin\widehat {ABH} = \frac{{AH}}{{AB}}$.

$B’G = BG \cdot tan{60^ \circ } = a\frac{{\sqrt 3 }}{2} \cdot \frac{2}{3} \cdot \sqrt 3 = a$.

$B’M = \sqrt {B'{G^2} + G{M^2}} = \sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2} \cdot \frac{1}{3}} \right)}^2}} = \frac{{a\sqrt {39} }}{6}$.

Ta có $\vartriangle AHM \sim \Delta B’GM \Rightarrow AH = \frac{{AM \cdot B’G}}{{B’M}} = \frac{{a \cdot \frac{{a\sqrt 3 }}{2}}}{{\frac{{a\sqrt {39} }}{6}}} = \frac{{3a}}{{\sqrt {13} }}$.

Vậy $sin\widehat {ABH} = \frac{{\frac{{3a}}{{\sqrt {13} }}}}{a} = \frac{3}{{\sqrt {13} }}$.

Câu 50: Cho hình chóp $S \cdot ABC$ có đáy $ABC$ là tam giác vuông cân tại $B,AB = a,SA \bot AB,SC \bot BC$, $SB = 2a$. Gọi $M,N$ lần lượt là trung điểm $SA,BC$. Gọi $\alpha $ là góc giữa $MN$ với $\left( {ABC} \right)$. Tính $cos\alpha $.

A. $cos\alpha = \frac{{2\sqrt {11} }}{{11}}$.

B. $cos\alpha = \frac{{\sqrt 6 }}{3}$.

C. $cos\alpha = \frac{{2\sqrt 6 }}{5}$.

D. $cos\alpha = \frac{{\sqrt {10} }}{5}$.

Lời giải

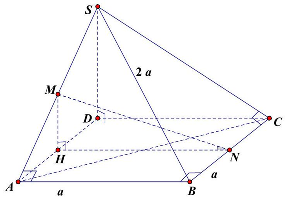
Gọi $D$ là hình chiếu của $S$ lên $\left( {ABC} \right)$, ta có:

$\left\{ {\begin{array}{*{20}{l}}
{BC \bot SC} \\
{BC \bot SD}
\end{array} \Rightarrow BC \bot CD$ và $\left\{ {\begin{array}{*{20}{l}}
{AB \bot SA} \\
{AB \bot SD}
\end{array} \Rightarrow AB \bot AD} \right.} \right..\;$

Mà $ABC$ là tam giác vuông cân tại $B$ nên $ABCD$ là hình vuông.

Gọi $H$ là trung điểm của $AD$, ta có $MH//SD$ mà $ \Rightarrow MH \bot \left( {ABCD} \right)$.

Do đó $HN$ là hình chiếu của $MN$ lên $\left( {ABC} \right)$.

$ \Rightarrow \alpha = \left( {MN,\left( {ABC} \right)} \right) = \left( {MN,NH} \right) = \overline {MNH} $

$SC = \sqrt {S{B^2} – B{C^2}} = \sqrt {4{a^2} – {a^2}} = a\sqrt 3 .$

$SD = \sqrt {S{C^2} – D{C^2}} = \sqrt {3{a^2} – {a^2}} = a\sqrt 2 .$

$tan\alpha = \frac{{MH}}{{NH}} = \frac{{\frac{1}{2} \cdot SD}}{{AB}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{a} = \frac{{\sqrt 2 }}{2}.$

$ \Rightarrow cos\alpha = \sqrt {\frac{1}{{1 + ta{n^2}\alpha }}} = \sqrt {\frac{1}{{1 + \frac{1}{2}}}} = \frac{{\sqrt 6 }}{3}.$

Câu 51: Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là điểm trên đoạn $SD$ sao cho $SM = 2MD$.

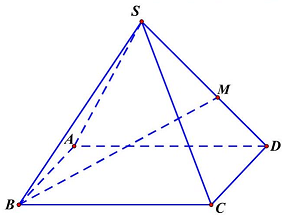
Tan góc giữa đường thẳng $BM$ và mặt phẳng $\left( {ABCD} \right)$ là

A. $\frac{1}{3}$.

B. $\frac{{\sqrt 5 }}{5}$.

C. $\frac{{\sqrt 3 }}{3}$.

D. $\frac{1}{5}$.

Lời giải

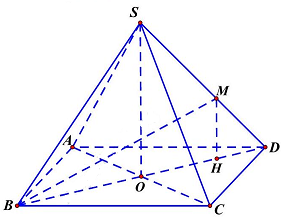
Ta có $BD = a\sqrt 2 \Rightarrow OD = \frac{{a\sqrt 2 }}{2}$.

Xét tam giác $SOD$ vuông tại $O$ có: $SO = \sqrt {S{D^2} – O{D^2}} = \sqrt {{a^2} – {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}$.

Kẻ $MH \bot BD$ tại $H$ nên $\left( {BM;\left( {ABCD} \right)} \right) = \widehat {MBH}$

Do $MH \bot BD \Rightarrow MH//SO$. Ta có $\frac{{MH}}{{SO}} = \frac{{MD}}{{SD}} = \frac{{HD}}{{OD}} = \frac{1}{3}$.

$ \Rightarrow MH = \frac{{SO}}{3} = \frac{{a\sqrt 2 }}{6}$ và $HD = \frac{1}{3}OD = \frac{{a\sqrt 2 }}{6} \Rightarrow BH = BD – HD = a\sqrt 2 – \frac{{a\sqrt 2 }}{6} = \frac{{5a\sqrt 2 }}{6}$.

Xét tam giác $BHM$ vuông tại $H$ có:

$tan\left( {BM;\left( {ABCD} \right)} \right) = \widehat {MBH} = \frac{{MH}}{{BH}} \Rightarrow tan\left( {BM;\left( {ABCD} \right)} \right) = \frac{1}{5}$

Câu 52: Cho hình chóp tam giác đều $S.ABC$ có độ dài cạnh đáy bằng $a$. Độ dài cạnh bên của hình chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng ${60^ \circ }$.

A. $\frac{{2a}}{{\sqrt 3 }}$.

B. $\frac{a}{6}$.

C. $\frac{{a\sqrt 3 }}{6}$.

D. $\frac{{2a}}{3}$.

Lời giải

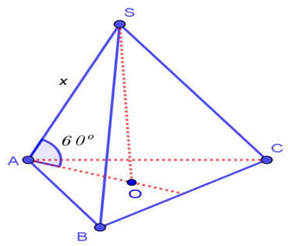
Đặt $SA = x$.

Gọi $O$ là tâm của tam giác đều $ABC \Rightarrow SO \bot \left( {ABC} \right)$.

Hình chiếu của $SA$ trên mặt phẳng $\left( {BCD} \right)$ là $AO \Rightarrow $ góc giữa cạnh bên $SA$ và mặt đáy là góc

$\widehat {SAO} = {60^ \circ }.\;$

Xét tam giác vuông $SAO:cos{60^ \circ } = \frac{{AO}}{{SA}} \Rightarrow SA = \frac{{AO}}{{cos{{60}^ \circ }}} = \frac{{\frac{{a\sqrt 3 }}{3}}}{{\frac{1}{2}}} = \frac{{2a}}{{\sqrt 3 }}$.

Câu 53: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với đáy, cạnh bên $SB$ tạo với đáy góc ${45^ \circ }$. Một mặt phẳng $\left( \alpha \right)$ đi qua $A$ và vuông góc với $SC$ cắt hình chóp $S.ABCD$ theo thiết diện là tứ giác $AB’C’D’$ có diện tích bằng:

A. $\frac{{{a^2}\sqrt 3 }}{4}$.

B. $\frac{{{a^2}\sqrt 3 }}{2}$.

C. $\frac{{{a^2}\sqrt 3 }}{6}$.

D. $\frac{{{a^2}\sqrt 3 }}{3}$.

Lời giải

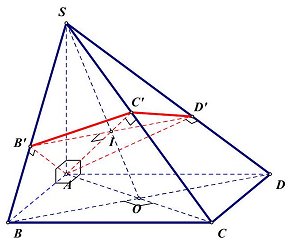
Dễ thấy $\widehat {SBA} = {45^ \circ }$. Ta có $B’D’ \bot SC$ và $BD \bot SC$ và $SC$ không vuông góc với mặt phẳng $\left( {SBD} \right)$, suy ra $BD//B’D’$. Nên từ $I = SO \cap AC’$ nên từ $I$ kẻ $B’D’//BD$ cắt $SB,SD$ lần lượt tại $B’,D’$.

Từ trên suy ra $B’D’ \bot AC’$ và $\left\{ {\begin{array}{*{20}{l}}
{AB’ \bot SC} \\
{AB’ \bot BC}
\end{array} \Rightarrow AB’ \bot SB} \right.$.

Suy ra ${S_{AB’C’D’}} = \frac{1}{2}AC’ \cdot B’D’$. Mà $AC’ = \frac{{a\sqrt 6 }}{3}$ và $\frac{{B’D’}}{{BD}} = \frac{{SB’}}{{SB}} = \frac{{a\sqrt 2 }}{{2 \cdot a\sqrt 2 }} = \frac{1}{2} \Rightarrow B’D’ = \frac{{a\sqrt 2 }}{2}$.

Vậy ${S_{AB’C’D’}} = \frac{1}{2}AC’ \cdot B’D’ = \frac{{\sqrt 3 }}{6}{a^2}$.