Trắc Nghiệm Đường Thẳng Vuông Góc Với Mặt Phẳng Mức Vận Dụng Giải Chi Tiết

Trắc nghiệm đường thẳng vuông góc với mặt phẳng mức vận dụng giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.
Câu 1. Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$ và đáy $ABCD$ là hình vuông tâm $O$; Gọi $I$ là trung điểm của $SC$; Xét các khẳng định sau:

1. $OI \bot \left( {ABCD} \right)$.

2. $BD \bot SC$.

3. $\left( {SAC} \right)$ là mặt phẳng trung trực của đoạn $BD$.

4. $SB = SC = SD$.

Trong bốn khẳng định trên, số khẳng định sai là

A. 1 .

B. 4 .

C. 2 .

D. 3 .

Lời giải

Chọn A

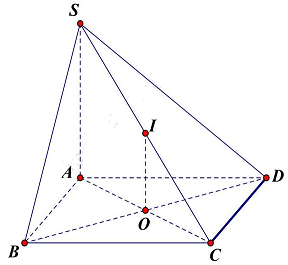
Xét khẳng định 1 ,

Ta có: $OI$ là đường trung bình trong tam giác $SAC$ nên $OI//SA$, mà $SA \bot \left( {ABCD} \right)$ suy ra $OI \bot \left( {ABCD} \right)$. Khẳng định 1 đúng.

Xét khẳng định 2, Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot SC} \right.$. Khẳng định 2 đúng.

Xét khẳng định 3, Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BD \cap \left( {SAC} \right) = O} \\
{BD \bot \left( {SAC} \right)}
\end{array},O} \right.$ là trung điểm của $BD$. Khẳng định 3 đúng.

Xét khẳng định 4, Ta có: $\left\{ {\begin{array}{*{20}{l}}
{S{B^2} = S{A^2} + A{B^2}} \\
{S{C^2} = S{A^2} + A{C^2}} \\
{S{D^2} = S{A^2} + A{D^2}} \\
{AB \ne AC}
\end{array} \Rightarrow SB = SD \ne SC} \right.$. Khẳng định 4 sai.

Vậy trong các khẳng định trên số khẳng định sai là 1.

Câu 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nữa lục giác đều với cạnh $a$. Cạnh $SA$ vuông góc với đáy và $SA = a\sqrt 3 .M$ là một điểm khác $B$ và ở trên $SB$ sao cho $AM$ vuông góc với $MD$. Khi đó, tỉ số $\frac{{SM}}{{SB}}$ bằng

A. $\frac{3}{4}$.

B. $\frac{2}{3}$.

C. $\frac{3}{8}$.

D. $\frac{1}{3}$.

Lời giải

Chọn A

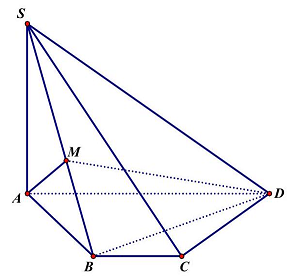
Áp dụng tính chất nửa lục giác đều, ta có $BD \bot AB$.

Mặt khác, $BD \bot SA$. Suy ra $BD \bot \left( {SAB} \right)$, ta được $BD \bot AM$.

Kết hợp $AM \bot MD$, ta được $AM \bot \left( {SBD} \right)$. Suy ra $AM \bot SB$.

Khi đó $\frac{{SM}}{{SB}} = \frac{{SM \cdot SB}}{{S{B^2}}} = \frac{{S{A^2}}}{{S{B^2}}} = \frac{{3{a^2}}}{{4{a^2}}} = \frac{3}{4}$.

$O$ trên mặt phẳng $\left( {ABC} \right)$.

$AH \bot BC$ nên $H$ là trực tâm của tam giác $ABC$.

Câu 3. Cho hình chóp $S.ABCD$, đáy $ABCD$ là hình thang vuông tại $A,B.SA$ vuông góc với đáy, $M$ là một điểm trên cạnh $AB$. Gọi $\left( P \right)$ là mặt phẳng qua $M$ và song song với $SA,AD$. Thiết diện của hình chóp với mặt phẳng $\left( P \right)$ là

A. Hình bình hành.

B. Hình vuông.

C. Hình thang vuông.

D. Hình chữ nhật.

Lời giải

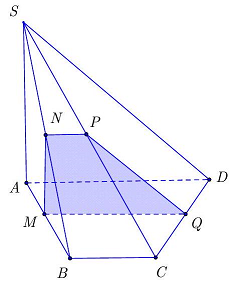
Do $\left( P \right)//SA$ và $M \in \left( {SAB} \right) \cap \left( P \right)$ nên $\left( P \right) \cap \left( {SAB} \right) = MN$ (với $N \in SB;MN//SA$ ).

Do $\left( P \right)//AD$ và $M \in \left( {ABCD} \right) \cap \left( P \right)$ nên $\left( P \right) \cap \left( {ABCD} \right) = MQ$ (với $Q \in BC;MQ//AD$ ).

Do $\left( P \right)//AD$ và $N \in \left( {SBC} \right) \cap \left( P \right)$ nên $\left( P \right) \cap \left( {SBC} \right) = NP$ (với $P \in SC$; $NP//AD//BC$ ).

Vậy thiết diện là hình thang vuông $MNPQ$.

Câu 4. Cho hình hộp đứng $ABCD \cdot A’B’C’D’$ có đáy $ABCD$ là hình vuông cạnh $a,AA’ = 3a$. Mặt phẳng qua $A$ vuông góc với $A’C$ cắt các cạnh $BB’,CC’,DD’$ lần lượt tại $I,J,K$. Tính diện tích thiết diện $AIJK$

A. $\frac{{2{a^2}\sqrt {11} }}{3}$.

B. $\frac{{{a^2}\sqrt {11} }}{2}$.

C. $\frac{{{a^2}\sqrt {11} }}{3}$.

D. $\frac{{3{a^2}\sqrt {11} }}{2}$.

Lời giải

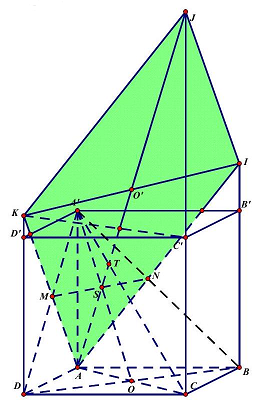
Dựng $AM \bot A’D$ ta có $AM \bot \left( {A’DC} \right) \Rightarrow AM \bot A’C$,

Tương tự, dựng $AN \bot A’B$ ta có $AN \bot \left( {A’BC} \right) \Rightarrow AN \bot A’C$.

Vậy mặt phẳng thỏa mãn yêu cầu bài toán là mặt phẳng $\left( {AMN} \right)$.

Kéo dài $AM \cap DD’ = \left\{ K \right\},AN \cap BB’ = \left\{ I \right\}$, và $AS \cap CC’ = \left\{ J \right\}$ với $\left\{ S \right\} = MN \cap A’C$.

Thiết diện $AIJK$ là thiết diện cần tìm.

Dễ thấy $ABCD$ là hình chiếu vuông góc của $AIJK$ lên mặt phẳng $\left( {ABCD} \right)$.

Ta có ${S_{ABCD}} = {S_{AIJK}} \cdot {\text{cos}}\left( {\left( {ABCD} \right),\left( {AIJK} \right)} \right)$.

Dễ thấy góc giữa hai mặt $\left( {AIJK} \right)$ và $\left( {ABCD} \right)$ là góc giữa hai đường $A’A\& A’C$ và là góc $\widehat {AA’C}$.

Xét tam giác vuông $A’AC\left( {\hat A = 1v} \right)$ có ${\text{cos}}\widehat {AA’C} = \frac{{A’A}}{{A’C}} = \frac{{3a}}{{a\sqrt {11} }} = \frac{3}{{\sqrt {11} }}$.

Vậy ${S_{AIJK}} = \frac{{{S_{ABCD}}}}{{{\text{cos}}\left( {\left( {ABCD} \right),\left( {AIJK} \right)} \right)}} \Rightarrow {S_{AIJK}} = \frac{{{a^2}\sqrt {11} }}{3}$.

Câu 5. Cho hình chóp đều $S.ABC$ có đáy $ABC$ là tam giác đều cạnh bằng $2a$, các mặt bên là các tam giác vuông cân tại $S$. Gọi $G$ là trọng tâm của $\vartriangle ABC,\left( \alpha \right)$ là mặt phẳng qua $G$ vuông góc với $SC$. Diện tích thiết diện của hình chóp $S.ABC$ khi cắt bởi mặt phẳng $\left( \alpha \right)$ bằng

A. $\frac{4}{9}{a^2}$.

B. $\frac{2}{3}{a^2}$.

C. $\frac{4}{3}{a^2}$.

D. $\frac{2}{9}{a^2}$.

Lời giải

Chọn A

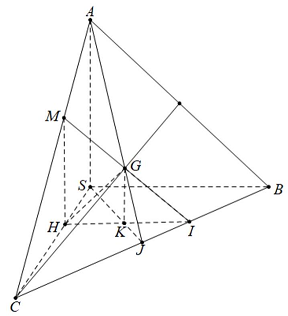
Xét $\vartriangle SBC$ vuông cân tại $S,BC = 2a$ ta có:

$S{B^2} + S{C^2} = B{C^2} \Leftrightarrow 2S{B^2} = 4{a^2} \Leftrightarrow S{B^2} = 2{a^2} \Rightarrow SB = a\sqrt 2 = SA = SC$.

Gọi $J$ là trung điểm của $BC$, trong $\left( {SJA} \right)$ kẻ $GK//SA$ cắt $SJ$ tại $K$.

Trong $\left( {SBC} \right)$ kẻ đường thẳng qua $K$ song song với $SB$ cắt $SC$ và $CB$ lần lượt tại $H$ và $I$.

Trong $\left( {SAC} \right)$ kẻ $HM//SA$ cắt $SC$ tại $M$.

Do các mặt bên của hình chóp $S.ABC$ là các tam giác vuông tại $S$ nên ta có:

$\left\{ {\begin{array}{*{20}{l}}
{SA \bot SC} \\
{SA \bot SB}
\end{array} \Rightarrow SA \bot \left( {SBC} \right)} \right.$ mà $GK//SA \Rightarrow GK \bot \left( {SBC} \right) \Rightarrow GK \bot SC$ (1).

Do $\left\{ {\begin{array}{*{20}{l}}
{SB \bot SC} \\
{IH//SB}
\end{array} \Rightarrow IH \bot SC\left( 2 \right)} \right.$.

Từ (1) và (2) $ \Rightarrow SC \bot \left( {HMI} \right)$. Vậy thiết diện là $\Delta HMI$.

Ta có: $KG//SA;KJ//SB$ và do $G$ là trọng tâm $\vartriangle ABC$ nên $\frac{{JG}}{{JA}} = \frac{{JK}}{{JS}} = \frac{{JI}}{{JB}} = \frac{1}{3} \Rightarrow \frac{{CI}}{{CB}} = \frac{2}{3}$.

Mặt khác: $HI//SB;HM//SA$ nên ta có:

$\frac{2}{3} = \frac{{CI}}{{CB}} = \frac{{HI}}{{SB}} \Rightarrow HI = \frac{2}{3}SB = \frac{{2a\sqrt 2 }}{3}$

$\frac{2}{3} = \frac{{CI}}{{CB}} = \frac{{CH}}{{CS}} = \frac{{HM}}{{SA}} \Rightarrow HM = \frac{2}{3}SA = \frac{{2a\sqrt 2 }}{3}$

Do $SB \bot (\left( {SAC} \right);HI//SB \Rightarrow HI \bot \left( {SAC} \right) \Rightarrow HI \bot MH \Rightarrow \Delta HMI$ vuông tại $H$.

Diện tích $\vartriangle HIM$ là: ${S_{\Delta HIM}} = \frac{1}{2}HM \cdot HI = \frac{1}{2} \cdot {\left( {\frac{{2\sqrt 2 a}}{3}} \right)^2} = \frac{{4{a^2}}}{9}$.

Câu 6. Cho lăng trụ đều $ABC \cdot A’B’C’$ có cạnh đáy bằng $a$, cạnh bên bằng $a\sqrt 2 $. Gọi $M$ là trung điểm của $AB$. Diện tích thiết diện cắt lăng trụ đã cho bởi mặt phẳng $\left( {A’C’M} \right)$ là

A. $\frac{{7\sqrt 2 }}{{16}}{a^2}$.

B. $\frac{{3\sqrt {35} }}{{16}}{a^2}$.

C. $\frac{{3\sqrt 2 }}{4}{a^2}$.

D. $\frac{9}{8}{a^2}$.

Lời giải

Chọn B

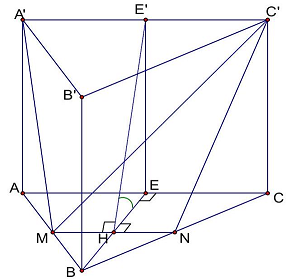
Gọi $N$ là trung điểm $BC$. Kẻ $MN//AC \Rightarrow MN//A’C’$

Mặt phẳng $\left( {A’C’M} \right)$ cắt lăng trụ theo thiết diện là hình thang $A’C’NM$.

Gọi $E,E’$ lần lượt là trung điểm $AC$ và $A’C’$. Gọi $H$ là giao điểm của $MN$ và $BE$

Ta dễ dàng chứng minh $MN \bot \left( {E’HE} \right)$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{\left( {A’C’NM} \right) \cap \left( {ABC} \right) = MN} \\
{EH \bot MN} \\
{E’H \bot MN}
\end{array}} \right.$

$ \Rightarrow \left( {\widehat {\left. {\left( {A’C’NM} \right),\left( {ACNM} \right)} \right)} = \widehat {\left( {HE,HE’} \right)} = \widehat {E’HE} = \varphi } \right.$

Ta có $BE = \frac{{a\sqrt 3 }}{2} \Rightarrow HE = \frac{{a\sqrt 3 }}{4}.E’H$

$ = \sqrt {E'{E^2} + E{H^2}} = \sqrt {2{a^2} + \frac{{3{a^2}}}{{16}}} = \frac{{a\sqrt {35} }}{4}$

Từ đó ${\text{cos}}\varphi = \frac{{HE}}{{HE’}} = \frac{{a\sqrt 3 }}{4} \cdot \frac{4}{{a\sqrt {35} }} = \frac{{\sqrt 3 }}{{\sqrt {35} }}$

Diện tích hình thang cân ${S_{ACNM}} = \frac{{\left( {MN + AC} \right) \cdot HE}}{2} = \frac{{\left( {\frac{a}{2} + a} \right)\frac{{a\sqrt 3 }}{4}}}{2} = \frac{{3{a^2}\sqrt 3 }}{{16}}$

Ta có ${S_{ACNM}} = {S_{A’C’NM}} \cdot {\text{cos}}\varphi ,$.

$ \Rightarrow {S_{A’C’NM}} = \frac{{{S_{ACNM}}}}{{{\text{cos}}\varphi }} = \frac{{3{a^2}\sqrt 3 }}{{16}} \cdot \frac{{\sqrt {35} }}{{\sqrt 3 }} = \frac{{3{a^2}\sqrt {35} }}{{16}}$

Câu 7. Cho hình chóp $S.ABCD$ với đáy $ABCD$ là hình thang vuông tại $A$, đáy lớn $AD = 8$, đáy nhỏ $BC = 6.SA$ vuông góc với đáy, $SA = 6$. Gọi $M$ là trung điểm của $AB.\left( P \right)$ là mặt phẳng qua $M$ và vuông góc với $AB$. Thiết diện của hình chóp $S.ABCD$ cắt bởi mặt phẳng $\left( P \right)$ có diện tích bằng:

A. 20 .

B. 15 .

C. 30 .

D. 16 .

Lời giải

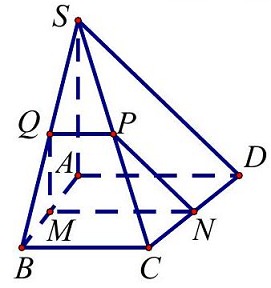
Ta có $\left. {\begin{array}{*{20}{c}}
{AB \bot SA} \\
{AB \bot AD}
\end{array}} \right\} \Rightarrow AB \bot \left( {SAD} \right)$. Mà $\left( P \right)$ qua $M$ và vuông góc với $AB$ nên $\left( P \right)//\left( {SAD} \right)$

$ \Rightarrow \left( P \right)//SA,\left( P \right)//AD$ và \left( P \right)//SD$

Trong mặt phẳng $\left( {SAB} \right)$ kẻ $MQ//SA$ với $Q \in SB$.

Trong mặt phẳng $\left( {ABCD} \right)$ kẻ $MN//AD$ với $N \in CD$.

Trong mặt phẳng $\left( {SCD} \right)$ kẻ $NP//SD$ với $P \in SC$.

Vì $M$ là trung điểm của $AB$ nên $N,P,Q$ lần lượt là trung điểm của các cạnh $CD,SC,SB$.

Do đó thiết diện là hình thang $MNPQ$ vuông tại $Q$ và $M$.

Ta có $MN = \frac{1}{2}\left( {AD + BC} \right) = \frac{1}{2}\left( {8 + 6} \right) = 7\;MQ = \frac{1}{2}SA = 3\;PQ = \frac{1}{2}BC = 3$

Vậy diện tích của thiết diện là : ${S_{MNPQ}} = \frac{{\left( {MN + PQ} \right) \cdot QM}}{2} = \frac{{\left( {7 + 3} \right) \cdot 3}}{2} = 15$.

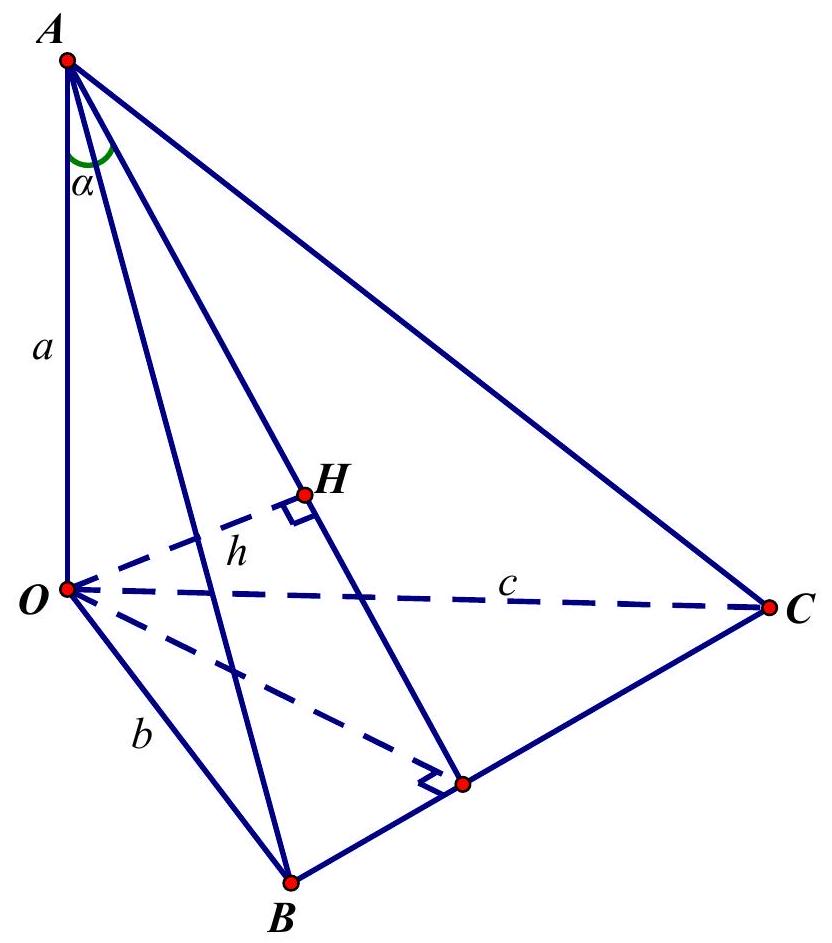
Câu 8. Xét tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc. Gọi $\alpha ,\beta ,\gamma $ lần lượt là góc giữa các đường thẳng $OA,OB,OC$ với mặt phẳng $\left( {ABC} \right)$ (hình vẽ).

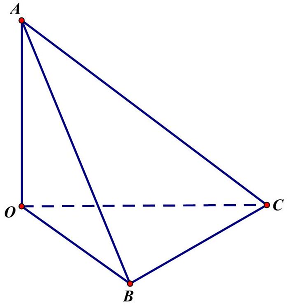
Khi đó giá trị nhỏ nhất của biểu thức $M = \left( {3 + {\text{co}}{{\text{t}}^2}\alpha } \right) \cdot \left( {3 + {\text{co}}{{\text{t}}^2}\beta } \right) \cdot \left( {3 + {\text{co}}{{\text{t}}^2}\gamma } \right)$ là

A. Số khác.

B. $48\sqrt 3 $.

C. 48 .

D. 125 .

Lời giải

Gọi $H$ là trực tâm tam giác $ABC$, vì tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc nên ta có $OH \bot \left( {ABC} \right)$ và $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$.

Ta có $\alpha = \widehat {\left( {OA;\left( {ABC} \right)} \right)} = \widehat {OAH},$

$\beta = \widehat {\left( {OB;\left( {ABC} \right)} \right)} = \widehat {OBH},\gamma = \widehat {\left( {OC;\left( {ABC} \right)} \right)} = \widehat {OCH}$

Nên ${\text{sin}}\alpha = \frac{{OH}}{{OA}},{\text{sin}}\beta = \frac{{OH}}{{OB}},{\text{sin}}\gamma = \frac{{OH}}{{OC}}$.

Đặt $a = OA,b = OB,c = OC,h = OH$ thì $\frac{1}{{{h^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}$ và

$M = \left( {3 + {\text{co}}{{\text{t}}^2}\alpha } \right) \cdot \left( {3 + {\text{co}}{{\text{t}}^2}\beta } \right) \cdot \left( {3 + {\text{co}}{{\text{t}}^2}\gamma } \right)$

$ = \left( {2 + \frac{1}{{{\text{si}}{{\text{n}}^2}\alpha }}} \right) \cdot \left( {2 + \frac{1}{{{\text{si}}{{\text{n}}^2}\beta }}} \right) \cdot \left( {2 + \frac{1}{{{\text{si}}{{\text{n}}^2}\gamma }}} \right)$

$ = \left( {2 + \frac{{{a^2}}}{{{h^2}}}} \right) \cdot \left( {2 + \frac{{{b^2}}}{{{h^2}}}} \right) \cdot \left( {2 + \frac{{{c^2}}}{{{h^2}}}} \right)$

$ = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right) \cdot \frac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right) \cdot \frac{1}{{{h^4}}} + {a^2}{b^2}{c^2} \cdot \frac{1}{{{h^6}}}.$

Ta có: $\left( {{a^2} + {b^2} + {c^2}} \right) \cdot \frac{1}{{{h^2}}} = \left( {{a^2} + {b^2} + {c^2}} \right) \cdot \left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)$

$ \geqslant 3\sqrt[3]{{{a^2} \cdot {b^2} \cdot {c^2}}} \cdot 3\sqrt[3]{{\frac{1}{{{a^2}}} \cdot \frac{1}{{{b^2}}} \cdot \frac{1}{{{c^2}}}}} = 9$

${a^2}{b^2}{c^2} \cdot \frac{1}{{{h^6}}} = {a^2}{b^2}{c^2} \cdot {\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)^3} \geqslant {a^2}{b^2}{c^2} \cdot {\left( {\sqrt[3]{{\left( {\frac{1}{{{a^2}}} \cdot \frac{1}{{{b^2}}} \cdot \frac{1}{{{c^2}}}} \right)}}} \right)^3} = 27.$

$\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right) \cdot \frac{1}{{{h^4}}} = \left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right) \cdot {\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)^2}$

$ \geqslant 3\sqrt[3]{{{a^2}{b^2} \cdot {b^2}{c^2} \cdot {c^2}{a^2}}} \cdot {\left( {3\sqrt[3]{{\left( {\frac{1}{{{a^2}}} \cdot \frac{1}{{{b^2}}} \cdot \frac{1}{{{c^2}}}} \right)}}} \right)^2} = 3\sqrt[3]{{{a^4}{b^4}{c^4}}} \cdot 9\sqrt[3]{{\frac{1}{{{a^4}{b^4}{c^4}}}}} = 27$

Do đó:

$M = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right) \cdot \frac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right) \cdot \frac{1}{{{h^4}}} + {a^2}{b^2}{c^2} \cdot \frac{1}{{{h^6}}}$

$ \geqslant 8 + 4.9 + 2.27 + 27 = 125.$

Dấu đẳng thức xảy ra khi và chỉ khi $a = b = c$, hay $OA = OB = OC$.

Vậy $minM = 125$.