Các Dạng Toán Về Thể Tích Khối Chóp Lớp 11 Giải Chi Tiết

Các dạng toán về thể tích khối chóp lớp 11 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
I. Phương pháp:

Phương pháp

Thể tích khối chóp $V = \frac{1}{3}\beta h$

Trong đó, $\beta $ là diện tích đáy; $h$ là chiều cao

Diện tích đa giác đáy thường gặp

II. Các dạng toán:

1. Thể tích khối chóp có cạnh bên vuông góc với đáy:

a) Thể tích của khối chóp có đáy là tam giác

Câu 1. Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$,$AB = a$ ,$AC = 2a$, cạnh bên $SA$ vuông góc với mặt đáy và $SA = a$ . Tính thể tích của khối chóp $S.ABC$.

Lời giải

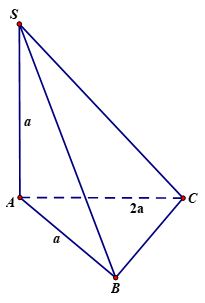
${V_{S.ABC}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABC}}.SA$

Tam giác $ABC$ vuông tại $A$

$ \Rightarrow $Diện tích đáy $B = {S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}a.2a = {a^2}$

Chiều cao: $h = a$

${V_{S.ABC}} = \frac{1}{3}{a^2}.a = \frac{{{a^3}}}{3}$

Câu 2. Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh , cạnh bên $SA$ vuông góc với mặt đáy và $SA = a$ . Tính thể tích của khối chóp $S.ABC$.

Lời giải

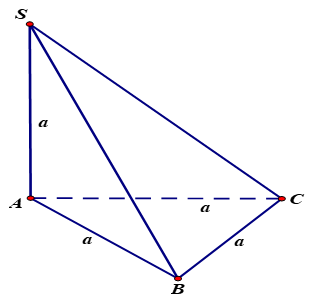
${V_{S.ABC}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABC}}.SA$

Tam giác ABC đều cạnh $a$

$ \Rightarrow $Diện tích đáy $B = {S_{ABC}} = \frac{{{{\left( {cạnh} \right)}^2}.\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}$

Chiều cao: $h = a$

${V_{S.ABC}} = \frac{1}{3}B.h = \frac{1}{3}\frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{{12}}$

Câu 3. Cho khối chóp $S.ABC$ có $SA$ vuông góc với $\left( {ABC} \right)$, đáy $ABC$ là tam giác vuông cân tại $A$,$BC = 2a$ , $\widehat {SBA} = 30^\circ $. Tính thể tích khối chóp $S.ABC$.

Lời giải

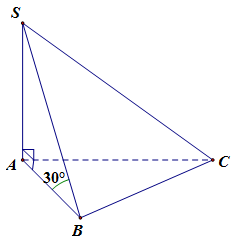
${V_{S.ABC}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABC}}.SA$

Tam giác $ABC$ vuông cân tại $A$, $BC = 2a$ $ \Rightarrow AB = AC = a\sqrt 2 $ .

Xét $\Delta SAB$ vuông tại $A$ có $SA = AB.\tan 30^\circ = a\sqrt 2 .\frac{{\sqrt 3 }}{3} = \frac{{a\sqrt 6 }}{3}$.

Ta có ${S_{ABC}} = \frac{1}{2}A{B^2} = {a^2}$.

Vậy ${V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SA = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}.{a^2} = \frac{{{a^3}\sqrt 6 }}{9}$ .

b) Thể tích của khối chóp có đáy là tứ giác

Câu 4. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật $AB = a$, $BC = 2a$, $SA = 2a$, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Tính thể tích khối chóp $S.ABCD$ tính theo $a$.

Lời giải

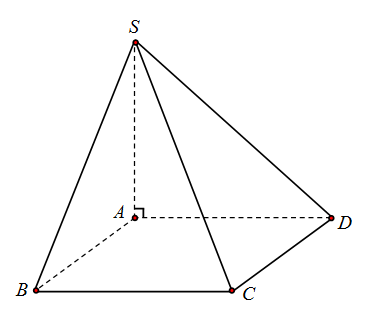
${V_{S.ABCD}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABCD}}.SA$

Ta có : $ABCD$ là hình chữ nhật

$ \Rightarrow $${S_{ABCD}} = AB.CD = a.2a$$ = 2{a^2}$.

Thể tích khối chóp $S.ABCD$ là ${V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SA$$ = \frac{1}{3}.2{a^2}.2a = \frac{{4{a^3}}}{3}$.

Câu 5. Cho khối chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, $SA$ vuông góc với đáy và $\widehat {CSB} = {30^0}$. Tính thể tích $V$ của khối chóp đã cho.

Lời giải

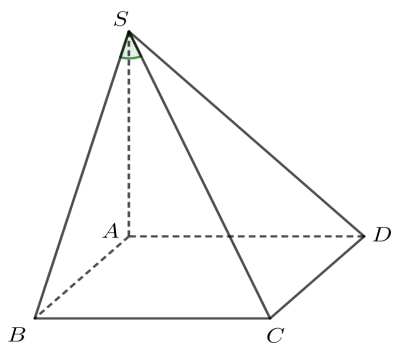
${V_{S.ABCD}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABCD}}.SA$

${S_{ABCD}} = {a^2}$

Tam giác $CSB$vuông tại $B$ có

$\tan \widehat {CSB} = \frac{{BC}}{{SB}} \Rightarrow SB = \frac{{BC}}{{\tan \widehat {CSB}}} = \frac{a}{{\tan {{30}^0}}} = \frac{a}{{\frac{{\sqrt 3 }}{3}}} = a\sqrt 3 $

Tam giác $SAB$vuông tại $A$ có $SA = \sqrt {S{B^2} – A{B^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} – {a^2}} = a\sqrt 2 $

Thể tích khối chóp : $V = \frac{1}{3}{S_{ABCD}}.SA = \frac{1}{3}{a^2}.a\sqrt 2 = \frac{{\sqrt 2 {a^3}}}{3}$.

Câu 6. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$, cạnh $SB$ vuông góc với đáy và $\widehat {SAB} = {60^0}$. Tính thể tích khối chóp $S.ABCD$.

Lời giải

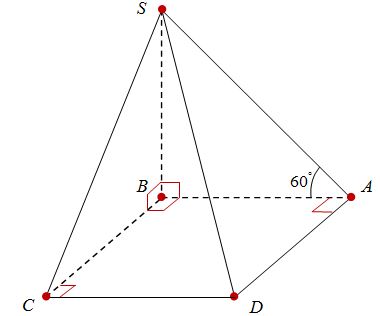
${V_{S.ABCD}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABCD}}.SB$

${S_{ABCD}} = {(2a)^2} = 4{a^2}$

Tam giác $SAB$vuông tại $A$ có :

$\tan \widehat {SBA} = \frac{{SB}}{{AB}}$$ \Rightarrow SB = AB.\tan {60^\circ } = 2a\sqrt 3 $

Vậy ${V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SB = \frac{1}{3}.4{a^2}.2a\sqrt 3 = \frac{{8{a^3}\sqrt 3 }}{3}$.

2. Thể tích khối chóp có mặt bên vuông góc với đáy:

Phương pháp:

$\left. \begin{gathered}
(P) \bot (Q) \hfill \\
(P) \cap (Q) = d \hfill \\
a \bot d \hfill \\
a \subset (P) \hfill \\
\end{gathered} \right\} \Rightarrow a \bot (Q)$

a) Thể tích của khối chóp có đáy là tam giác

Câu 1. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a$, tam giác $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp $S.ABC$.

Lời giải:

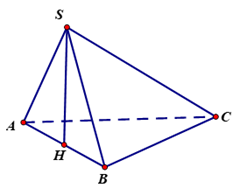
Xác định chiều cao hình chóp

Ta có: $\left( {SAB} \right) \bot \left( {ABC} \right)$

Kẻ $SH \bot AB$ tại $H$

$ \Rightarrow SH \bot \left( {ABC} \right)$

$ \Rightarrow {V_{S.ABC}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABC}}.SH$

Tính các yếu tố

$\Delta SAB$ là tam giác đều cạnh $2a$

$ \Rightarrow SH = \frac{{AB\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 $

$\Delta ABC$ là tam giác đều cạnh $2a$

$ \Rightarrow {S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{{(2a)}^2}.\sqrt 3 }}{4} = {a^2}\sqrt 3 $.

Vậy ${V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SH = \frac{1}{3}.{a^2}\sqrt 3 .a\sqrt 3 = {a^3}$.

Câu 2. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều; tam giác $SAB$ là tam giác vuông tại $S$ và nằm trong mặt phẳng vuông góc với mặt đáy. Biết $SA = 2a;\,SB = a\sqrt 3 $. Tính thể tích khối chóp $S.ABC$.

Lời giải:

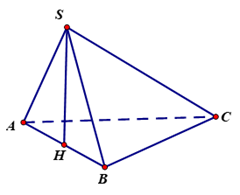
Xác định chiều cao hình chóp

Ta có: $\left( {SAB} \right) \bot \left( {ABC} \right)$

Kẻ $SH \bot AB$ tại $H$

$ \Rightarrow SH \bot \left( {ABC} \right)$

$ \Rightarrow {V_{S.ABC}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABC}}.SH$

Tính các yếu tố

$\Delta SAB$ là tam giác vuông tại $S$ với $AH$ là đường cao ta có:

$\frac{1}{{S{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{S{B^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{3{a^2}}} = \frac{7}{{12{a^2}}}$

$ \Rightarrow S{H^2} = \frac{{12{a^2}}}{7} \Rightarrow SH = \frac{{2a\sqrt {21} }}{7}$

$\Delta SAB$ là tam giác vuông tại $S$ ta có:

$AB = \sqrt {S{A^2} + A{B^2}} = \sqrt {4{a^2} + 3{a^2}} = a\sqrt 7 $

$\Delta ABC$ là tam giác đều cạnh $AB = a\sqrt 7 $

$ \Rightarrow {S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{{(a\sqrt 7 )}^2}.\sqrt 3 }}{4} = \frac{{7\sqrt 3 {a^2}}}{4}$.

Vậy ${V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SH = \frac{1}{3}.\frac{{7\sqrt 3 {a^2}}}{4}.\frac{{2a\sqrt {21} }}{7} = \frac{{{a^2}\sqrt 7 }}{2}$.

b) Thể tích của khối chóp có đáy là tứ giác

Câu 3. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy$\left( {ABCD} \right)$. Biết $SC = 2a\sqrt 3 $ và góc tạo bởi đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng ${30^0}$. Tính thể tích $V$của khối chóp $S.ABCD$.

Lời giải

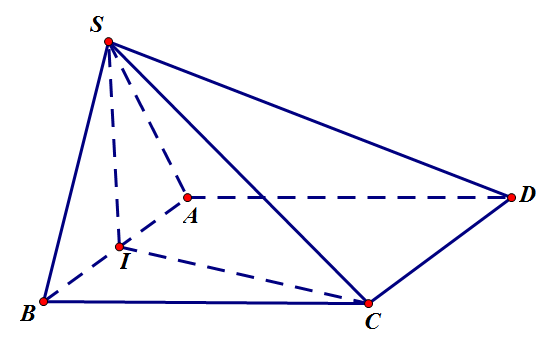Xác định chiều cao hình chóp

Ta có: $\left( {SAB} \right) \bot \left( {ABCD} \right)$

Kẻ $SI \bot AB$ tại $I$

$ \Rightarrow SI \bot \left( {ABCD} \right)$

$ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABCD}}.SI$

Tính các yếu tố

Xác định $\left( {\widehat {SC;\left( {ABCD} \right)}} \right)$.

Ta có: $IC$ là hình chiếu của $SC$ lên $(ABCD)$

$ \Rightarrow \left( {\widehat {SC;\left( {ABCD} \right)}} \right) = (SC;IC) = \widehat {SCI} = {30^0}$

Tam giác $SCI$vuông tại $I$ có $\sin \widehat {SCI} = \frac{{SI}}{{SC}}$

$ \Rightarrow SI = SC.\sin \widehat {SCI} = 2a\sqrt 3 .\sin {30^0} = a\sqrt 3 $

Tam giác $SCI$vuông tại $I$ có $co\operatorname{s} \widehat {SCI} = \frac{{CI}}{{SC}}$

$ \Rightarrow CI = SC.cos\widehat {SCI} = 2a\sqrt 3 .cos{30^0} = 3a$.

Tam giác $SAB$ đều có $SI = \frac{{AB\sqrt 3 }}{2}$

$ \Rightarrow AB = \frac{{2SI}}{{\sqrt 3 }} = \frac{{2.a\sqrt 3 }}{{\sqrt 3 }} = 2a$

Tam giác $CIB$vuông tại $B$ có $BC = \sqrt {C{I^2} – B{I^2}} = \sqrt {{{\left( {3a} \right)}^2} – {a^2}} = 2a\sqrt 2 $

$ \Rightarrow {S_{ABCD}} = AB.BC = 2a.2a\sqrt 2 = 4{a^2}\sqrt 2 $

Vậy ${V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SI = \frac{1}{3}.4{a^2}\sqrt 2 .a\sqrt 3 = \frac{{4{a^3}\sqrt 6 }}{3}$.

Câu 4. Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$, $\Delta SAD$ cân tại $S$ và nằm trong mặt phẳng vuông góc với đáy. Góc giữa $\left( {SBC} \right)$ và mặt đáy bằng ${60^o}$. Tính thể tích $S.ABCD$.

Lời giải

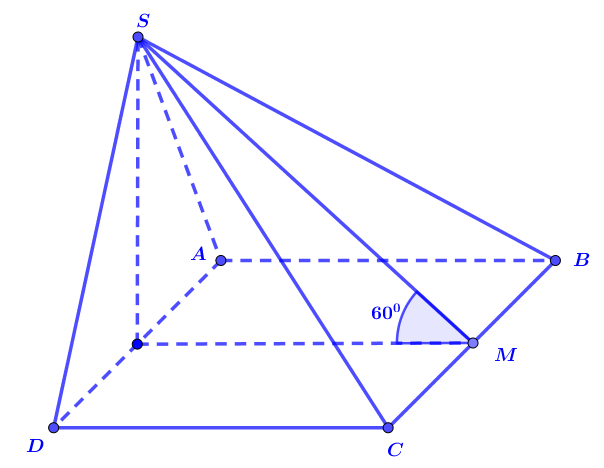
Xác định chiều cao hình chóp

Ta có: $\left( {SAD} \right) \bot \left( {ABCD} \right)$

Kẻ $SH \bot AD$ tại $H$

$ \Rightarrow SH \bot \left( {ABCD} \right)$

$ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}B.h = \frac{1}{3}{S_{ABCD}}.SH$

Tính các yếu tố

$ABCD$ là hình vuông cạnh $2a$ nên${S_{ABCD}} = A{B^2} = 4{a^2}$.

Gọi $M$ là trung điểm $BC$

Tam giác $SBC$ cân tại $S$ $ \Rightarrow SM \bot BC$

mà $HM \bot BC$

$ \Rightarrow $ $\left( {\widehat {\left( {SBC} \right);(ABCD)}} \right) = (SM;HM) = \widehat {SMH} = {60^0}$

Tam giác $SMH$vuông tại $H$ có $\tan \widehat {SMH} = \frac{{SH}}{{MH}}$

$ \Rightarrow SH = MH.\tan \widehat {SMH} = 2a.\tan {60^0} = 2a\sqrt 3 $.

Vậy ${V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{1}{3}.4{a^2}.2a\sqrt 3 = \frac{{8{a^3}\sqrt 3 }}{3}$.

3. Thể tích của khối chóp đều:

Phương pháp:

Hình chóp đều $ \Rightarrow $ đáy là đa giác đều và chân đường cao trùng với tâm của đáy

a) Thể tích của khối chóp đều có đáy là tam giác

Câu 1. Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và cạnh bên tạo đáy góc ${60^0}$. Thể tích của khối chóp đã cho.

Lời giải

Gọi $O$ là trọng tâm của tam giác $ABC$

Ta có $SO \bot \left( {ABC} \right)$.

$ \Rightarrow {V_{S.ABC}} = \frac{1}{3}{S_{đáy}}.h = \frac{1}{3}{S_{ABC}}.SO$

Tam giác $ABC$ đều cạnh $a$

Ta có: ${S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}$.

Xác định $\left( {\widehat {SA,\left( {ABC} \right)}} \right)$

Ta có $AO$ là hình chiếu của $SA$ lên mặt phẳng $\left( {ABC} \right)$.

Suy ra $\left( {\widehat {SA,\left( {ABC} \right)}} \right) = \left( {SA,AO} \right) = \widehat {SAO} = {60^0}$.

Tam giác $ABC$ đều cạnh $a$có $AM = \frac{{a\sqrt 3 }}{2}$

Xét tam giác $SAO$ vuông tại $O$, ta có:

$\tan \widehat {SAO} = \frac{{SO}}{{AO}} \Rightarrow SO = AO.\tan \widehat {SAO} = \frac{2}{3}AM.\tan {60^0} = \frac{2}{3}.a.\frac{{\sqrt 3 }}{2}.\sqrt 3 = a$.

Vậy ${V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SO = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{{12}}$.

Câu 2. Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a\sqrt 3 $ , cạnh bên bằng $2a$. Tính thể tích $V$của khối chóp $S.ABC$.

Lời giải

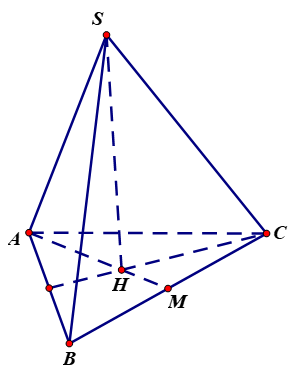
Gọi $H$ là trọng tâm của tam giác $ABC$

Ta có $SH \bot \left( {ABC} \right)$.

$ \Rightarrow {V_{S.ABC}} = \frac{1}{3}{S_{đáy}}.h = \frac{1}{3}{S_{ABC}}.SH$

Diện tích đáy $B = {S_{ABC}} = \frac{{{{\left( {a.\sqrt 3 } \right)}^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{4}$ ;

Tam giác $ABC$ đều cạnh $a\sqrt 3 $có $AM = \frac{{a\sqrt 3 .\sqrt 3 }}{2} = \frac{{3a}}{2}$

$AH = \frac{2}{3}AM = \frac{2}{3}.\frac{{3a}}{2} = a$

Tam giác $SHA$vuông tại $H$có $SH = \sqrt {S{A^2} – A{H^2}} = \sqrt {4{a^2} – {a^2}} = a\sqrt 3 $

Vậy ${V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SH = \frac{1}{3}.\frac{{3{a^2}\sqrt 3 }}{4}.a\sqrt 3 = \frac{{3{a^3}}}{4}$

b) Thể tích của khối chóp có đáy là tứ giác

Câu 3. Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và cạnh bên tạo với mặt phẳng đáy một góc ${60^0}$. Tính thể tích $V$của khối chóp $S.ABCD$.

Lời giải

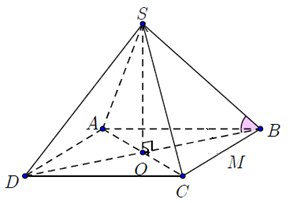
Gọi $O$ là tâm của hình vuông $ABCD$

Ta có $SO \bot \left( {ABCD} \right)$.

$ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}{S_{đáy}}.h = \frac{1}{3}{S_{ABCD}}.SO$

Ta có: $ABCD$ là hình vuông cạnh $a$ $ \Rightarrow {S_{ABCD}} = {a^2}$.

$\left( {\widehat {SB,\left( {ABC} \right)}} \right) = \left( {SB,OB} \right) = \widehat {SBO} = {60^0}$

$OB = \frac{1}{2}BD = \frac{1}{2}.a\sqrt 2 = \frac{{a\sqrt 2 }}{2}$ (Đường chéo hình vuông)

Xét tam giác $SBO$ vuông tại $O$, ta có $\tan \widehat {SBO} = \frac{{SO}}{{OB}}$

$ \Rightarrow SO = OB.\tan \widehat {SBO} = \frac{{a\sqrt 2 }}{2}.\tan {60^0} = \frac{{a\sqrt 6 }}{2}$.

Vậy ${V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.\frac{{a\sqrt 6 }}{2} = \frac{{{a^3}\sqrt 6 }}{6}$.

Câu 4. Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và mặt bên tạo với mặt phẳng đáy một góc ${60^0}$. Tính thể tích $V$của khối chóp $S.ABCD$.

Lời giải

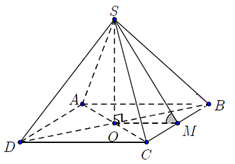
Gọi $O$ là tâm của hình vuông $ABCD$

Ta có $SO \bot \left( {ABCD} \right)$.

$ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}{S_{đáy}}.h = \frac{1}{3}{S_{ABCD}}.SO$

Ta có: $ABCD$ là hình vuông cạnh $a$ $ \Rightarrow {S_{ABCD}} = {a^2}$.

Gọi $M$ là trung điểm $BC$, góc giữa mặt bên $(SBC)$ và $(ABCD)$ là $\widehat {SMO} = {60^0}$

Ta có $OM = \frac{1}{2}AB = \frac{a}{2}.$

Xét tam giác $SOM$ vuông tại $O$, ta có $\tan \widehat {SMO} = \frac{{SO}}{{OM}}$

$SO = OM.\tan \widehat {SMO} = \frac{a}{2}.\tan {60^0} = \frac{{a\sqrt 3 }}{2}$.

Vậy ${V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{6}$.