Đề Cương Ôn Tập Giữa Học Kỳ 1 Toán 11 Kết Nối Tri Thức Giải Chi Tiết

Đề cương ôn tập giữa học kỳ 1 Toán 11 Kết nối tri thức giải chi tiết được soạn dưới dạng file word và PDF gồm 8 trang. Các bạn xem và tải về ở dưới.

PHẦN 1. TRẮC NGHIỆM

Câu 1: Cho $0 < \alpha < \frac{\pi }{2}$. Khẳng định nào sau đây đúng?

A. $sin\left( {\pi – \alpha } \right) > 0$.

B. $sin\left( {\pi – \alpha } \right) \geqslant 0$.

C. $sin\left( {\pi – \alpha } \right) < 0$.

D. $sin\left( {\pi – \alpha } \right) \leqslant 0$.

Chọn A

Lời giải

Ta có $0 < \alpha < \frac{\pi }{2} \Rightarrow \frac{\pi }{2} < \pi – \alpha < \pi $ nên $sin\left( {\pi – \alpha } \right) > 0$.

Câu 2: Cho $\frac{\pi }{2} < \alpha < \pi $. Khẳng định nào sau đây sai?

A. $sin\left( {\frac{\pi }{2} – \alpha } \right) < 0$.

B. $cos\left( {\frac{\pi }{2} – \alpha } \right) > 0$.

C. $tan\left( {\frac{\pi }{2} – \alpha } \right) > 0$.

D. $cot\left( {\frac{\pi }{2} – \alpha } \right) < 0$.

Lời giải

Chọn C

$tan\left( {\frac{\pi }{2} – \alpha } \right) = \cot \alpha < 0$

Câu 3: Một bánh xe có 48 răng. Số đo góc (tính bằng đơn vị radian với độ chính xác đến hàng phần nghìn) mà bánh xe đã quay được khi di chuyển 8 răng là.

A. 1,047 .

B. 1,048 .

C. 0,524 .

D. 0,523 .

Chọn A

Lời giải

Ta có : 48 răng ứng với $2\pi \left( {rad} \right)$ nên 8 răng ứng với $\frac{{8.2\pi }}{{48}} \approx 1,047197551 \approx 1,047$.

Câu 4: Độ dài $\ell $ của cung trên đường tròn có bán kính bằng $0,2\;m$ và số đo $\frac{\pi }{{16}}$ là.

A. $\ell = 3,93\;cm$.

B. $\ell = 2,94\;cm$.

C. $\ell = 3,39\;cm$.

D. $\ell = 1,49\;cm$.

Chọn A

Lời giải

Đổi $0,2\left( {\;m} \right) = 20\left( {\;cm} \right)$

Áp dụng công thức $\ell = R\alpha = 20 \cdot \frac{\pi }{{16}} \approx 3,926990817\left( {\;cm} \right) \approx 3,93\left( {\;cm} \right)$.

Câu 5: Độ dài $\ell $ của cung trên đường tròn có bán kính bằng $3\,cm$ và số đo ${120^0}$ là.

A. $\ell = 360\;cm$.

B. $\ell = 40\;cm$.

C. $\ell = 2\pi \;cm$.

D. $\ell = \pi \;cm$.

Lời giải

Chọn A

Đổi độ sang rad ta có: ${120^0} = {120^0}.\frac{\pi }{{{{180}^0}}} = \frac{{2\pi }}{3}$

Áp dụng công thức $\ell = R\alpha = 3 \cdot \frac{{2\pi }}{3} = \,2\pi \,cm$.

Câu 6: Trên đường tròn lượng giác gốc $A$ như hình vẽ dưới. Góc lượng giác $\frac{{27\pi }}{2}$có điểm biểu diễn là điểm nào dưới đây?

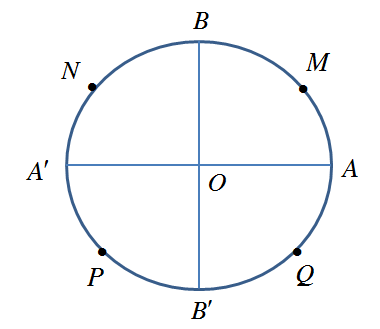
A. $A$.

B. $B$.

C. $A’$.

D. $B’$.

Lời giải

Chọn D

Ta có: $\frac{{27\pi }}{2} = \frac{{28\pi – \pi }}{2} = 14\pi – \frac{\pi }{2}$.

Góc lượng giác $\frac{{27\pi }}{2}$có điểm biểu diễn là điểm biểu diễn của góc $ – \frac{\pi }{2}$.

Vậy điểm biểu diễn là điểm $B’$.

Câu 7: Trên đường tròn lượng giác gốc $A$ như hình vẽ dưới. Góc lượng giác $\frac{{35\pi }}{4}$có điểm biểu diễn là điểm nào dưới đây?

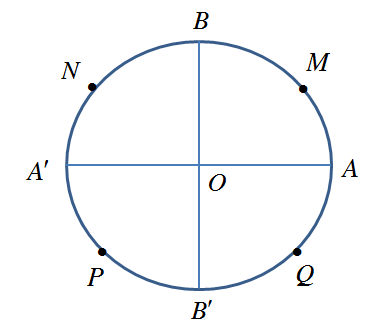
A. $M$.

B. $N$.

C. $P$.

D. $Q$.

Lời giải

Chọn B

Ta có: $\frac{{35\pi }}{4} = \frac{{32\pi + 3\pi }}{4} = 8\pi + \frac{{3\pi }}{4}$.

Do đó, góc lượng giác $\frac{{35\pi }}{4}$có điểm biểu diễn là điểm biểu diễn của góc $\frac{{3\pi }}{4}$.

Vậy điểm biểu diễn là điểm $N$

Câu 8: Góc lượng giác nào sau đây có cùng điểm cuối với góc $\frac{{7\pi }}{4}$ là.

A. $ – \frac{\pi }{4}$.

B. $\frac{\pi }{4}$.

C. $\frac{{3\pi }}{4}$.

D. $ – \frac{{3\pi }}{4}$.

Lời giải

Chọn A

Ta có: $\frac{{7\pi }}{4} = 2\pi – \frac{\pi }{4}$.

Góc lượng giác có cùng điểm cuối với góc $\frac{{7\pi }}{4}$ là $ – \frac{\pi }{4}$.

Câu 9: Trên đường tròn lượng giác gốc $A$, cho điểm $M$ xác định bởi . Gọi ${M_1}$ là điểm đối xứng của $M$ qua trục $Ox$. Tìm số đo của cung lượng giác $sd\left( {OA,O{M_1}} \right)$.

A. sđ $\frac{{ – 5\pi }}{3} + k2\pi ,k \in \mathbb{Z}$.

B. sd $\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}$.

C. sđ $\frac{{ – \pi }}{3} + k2\pi ,k \in \mathbb{Z}$.

D. sđ $\frac{{ – \pi }}{3} + k\pi ,k \in \mathbb{Z}$.

Chọn C

Lời giải

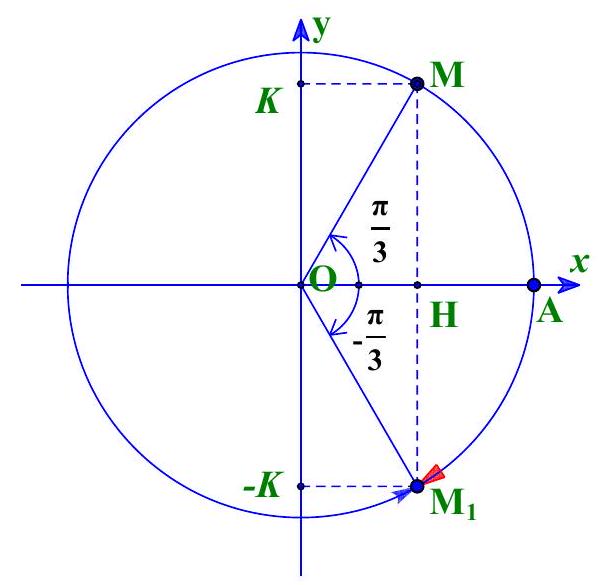
Vì ${M_1}$ là điểm đối xứng của $M$ qua trục $Ox$ nên có 1 góc lượng giác $\left( {OA,O{M_1}} \right) = – \frac{\pi }{3}$

$ \Rightarrow \frac{{ – \pi }}{3} + k2\pi ,k \in \mathbb{Z}$

Câu 10: Cho $0 < \alpha < \frac{\pi }{2}$. Mệnh đề nào sau đây đúng?

A. $sin\alpha < 0$.

B. $cos\left( {\alpha + \frac{\pi }{2}} \right) > 0$.

C. $tan\left( {\alpha + \pi } \right) < 0$.

D. $cot\alpha > 0$.

Lời giải

Chọn D

Với $0 < \alpha < \frac{\pi }{2}$, ta có: $sin\alpha > 0,cos\left( {\alpha + \frac{\pi }{2}} \right) < 0,\,tan\left( {\alpha + \pi } \right) > 0,cot\alpha > 0$.

Câu 11: Cho $cosa = \frac{1}{3}$, khi đó giá trị của $cos2a$ bằng:

A. $\frac{8}{9}$.

B. $\frac{7}{9}$.

C. $ – \frac{7}{9}$.

D. $ – \frac{8}{9}$.

Lời giải

Chọn C

Ta có $cos2a = 2co{s^2}a – 1 = \frac{2}{9} – 1 = – \frac{7}{9}$.

Câu 12: Cho $sina = – \frac{2}{3}$, khi đó giá trị của $cos2a$ bằng:

A. $\frac{8}{9}$.

B. $\frac{2}{9}$.

C. $\frac{4}{9}$.

D. $\frac{1}{9}$.

Lời giải

Chọn D

Ta có $cos2a = 1 – 2si{n^2}a = 1 – 2{\left( { – \frac{2}{3}} \right)^2} = \frac{1}{9}$.

Câu 13: Cho $sina + cosa = – \frac{4}{3}$, khi đó giá trị của $sin2a$ bằng:

A. $\frac{8}{9}$.

B. $\frac{7}{9}$.

C. $ – \frac{7}{9}$.

D. $ – \frac{8}{9}$.

Lời giải

Chọn B

$sina + cosa = – \frac{4}{3}\,\,(*)$

Bình phương hai vế của (*) ta được:

${\left( {sina + cosa} \right)^2} = {\left( { – \frac{4}{3}} \right)^2} \Leftrightarrow {\sin ^2}a + 2\sin a.\cos a + {\cos ^2}a = \frac{{16}}{9}$

$ \Leftrightarrow {\sin ^2}a + {\cos ^2}a + 2\sin a.\cos a = \frac{{16}}{9}$

$ \Leftrightarrow 1 + \sin 2a = \frac{{16}}{9} \Leftrightarrow \sin 2a = \frac{{16}}{9} – 1 \Leftrightarrow \sin 2a = \frac{7}{9}$

Câu 14: Cho $sina – cosa = \frac{1}{5}$, khi đó giá trị của $sin2a$ bằng:

A. $ – \frac{3}{{25}}$.

B. $\frac{3}{{25}}$.

C. $ – \frac{{24}}{{25}}$.

D. $\frac{{24}}{{25}}$.

Lời giải

Chọn D

$sina – cosa = \frac{1}{5}\,\,(*)$

Bình phương hai vế của (*) ta được:

${\left( {sina – cosa} \right)^2} = {\left( {\frac{1}{5}} \right)^2} \Leftrightarrow {\sin ^2}a – 2\sin a.\cos a + {\cos ^2}a = \frac{1}{{25}}$

$ \Leftrightarrow {\sin ^2}a + {\cos ^2}a – 2\sin a.\cos a = \frac{1}{{25}}$

$ \Leftrightarrow 1 – \sin 2a = \frac{1}{{25}} \Leftrightarrow \sin 2a = 1 – \frac{1}{{25}} \Leftrightarrow \sin 2a = \frac{{24}}{{25}}$

Câu 15: Cho $cos2x = \frac{{\sqrt 3 }}{2}$ với $0 < x < \frac{\pi }{2}$. Khi đó giá trị của $\sin x$ bằng

A. $\frac{{\sqrt 3 – \sqrt 6 }}{4}$.

B. $\frac{{\sqrt 6 – \sqrt 3 }}{4}$.

C. $\frac{{\sqrt 6 – \sqrt 2 }}{4}$.

D. $\frac{{\sqrt 2 – \sqrt 6 }}{4}$.

Lời giải

Chọn C

Ta có: ${\sin ^2}x = \frac{{1 – cos2x}}{2} = \frac{{1 – \frac{{\sqrt 3 }}{2}}}{2} = \frac{{2 – \sqrt 3 }}{4}$

$ \Rightarrow \sin x = \pm \sqrt {\frac{{2 – \sqrt 3 }}{4}} = \pm \frac{{\sqrt 6 – \sqrt 2 }}{4}$

Do $0 < x < \frac{\pi }{2}$ nên $\sin x > 0$

Vậy, $\sin x = \frac{{\sqrt 6 – \sqrt 2 }}{4}$

Câu 16: Cho hai góc $a$ và $b$ thỏa $tana = \frac{1}{7}$ và $tanb = \frac{3}{4}$. Tính $tan\left( {a + b} \right)$.

A. $\frac{{25}}{{28}}$.

B. 1 .

C. $ – \frac{{17}}{{28}}$.

D. $\frac{4}{{21}}$.

Lời giải

Chọn B

$tan\left( {a + b} \right) = \frac{{tana + tanb}}{{1 – tana \cdot tanb}} = \frac{{\frac{1}{7} + \frac{3}{4}}}{{1 – \frac{1}{7} \cdot \frac{3}{4}}} = 1.$

Câu 17: Cho hai góc $a$ và $b$ thỏa $tana = 2$ và $tanb = – 5$. Tính $tan\left( {a – b} \right)$.

A. $\frac{1}{3}$.

B. $ – \frac{1}{3}$ .

C. $\frac{7}{9}$.

D. $ – \frac{7}{9}$.

Lời giải

Chọn D

$tan\left( {a – b} \right) = \frac{{tana – tanb}}{{1 + tana \cdot tanb}} = \frac{{2 – ( – 5)}}{{1 + 2 \cdot ( – 5)}} = \frac{7}{{ – 9}} = – \frac{7}{9}.$

Câu 18: Cho góc $\alpha $ thỏa $\sin \alpha = – \frac{1}{3}$ với$\pi < \alpha < \frac{{3\pi }}{2}$. Tính $cos\left( {\alpha – \frac{\pi }{6}} \right)$ . (quy tròn đến hàng phần trăm)

A. $ – 0,98$.

B. $0,98$ .

C. $0,12$.

D. $ – 0,12$.

Lời giải

Chọn A

* Ta có $\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow cos\alpha < 0$

$ \Rightarrow cos\alpha = – \sqrt {1 – {{\sin }^2}\alpha } = – \sqrt {1 – {{\left( { – \frac{1}{3}} \right)}^2}} = – \frac{{2\sqrt 2 }}{3}$

Vậy $cos\left( {\alpha – \frac{\pi }{6}} \right) = cos\alpha cos\frac{\pi }{6} + \sin \alpha \sin \frac{\pi }{6}$

$ = – \frac{{2\sqrt 2 }}{3}.\frac{{\sqrt 3 }}{2} – \frac{1}{3}.\frac{1}{2} = – \frac{{2\sqrt 6 + 1}}{6} \approx – 0,98$

Câu 19: Cho góc $a,\,b$ thỏa $\sin a = – \frac{2}{3}$ với $\frac{{3\pi }}{2} < a < 2\pi $ và $cosb = \frac{1}{4}$ với $0 < b < \frac{\pi }{2}$. Tính $\sin \left( {a + b} \right)$ (quy tròn đến hàng phần trăm)

A. $ – 0,89$.
B. $0,56$.

C. $0,11$.

D. $ – 0,11$.

Lời giải

Chọn B

* Ta có $\frac{{3\pi }}{2} < \alpha < 2\pi \Rightarrow \cos a > 0$

$ \Rightarrow \cos a = \sqrt {1 – {{\sin }^2}a} = \sqrt {1 – {{\left( { – \frac{2}{3}} \right)}^2}} = \frac{{\sqrt 5 }}{3}$

* Ta có $0 < \alpha < \frac{\pi }{2} \Rightarrow \sin b > 0$

$ \Rightarrow \sin b = \sqrt {1 – co{s^2}b} = \sqrt {1 – {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt {15} }}{4}$

Vậy $\sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b$

$ = – \frac{2}{3}.\frac{1}{4} + \frac{{\sqrt 5 }}{3}.\frac{{\sqrt {15} }}{4} = \frac{{5\sqrt 3 – 2}}{{12}} \approx 0,56$

Câu 20: Thu gọn biểu thức $P = cos\alpha + cos3\alpha + cos5\alpha + \ldots + cos\left( {2n – 1} \right)\alpha $ với $n \in {\mathbb{N}^*},\alpha \ne k\pi \left( {k \in \mathbb{Z}} \right)$ ta được

A. $P = \frac{{sin2n\alpha }}{{2sin\alpha }}$.

B. $P = \frac{{sinn\alpha }}{{sin\alpha }}$.

C. $P = \frac{{cos2n\alpha }}{{2cos\alpha }}$.

D. $P = \frac{{cosn\alpha }}{{cos\alpha }}$.

Chọn A

Lời giải

Ta có: $2sin\alpha \cdot P = 2sin\alpha cos\alpha + 2sin\alpha cos3\alpha + 2sin\alpha cos5\alpha + \ldots + 2sin\alpha cos\left( {2n – 1} \right)\alpha $

$ \Leftrightarrow 2sin\alpha \cdot P = sin2\alpha + sin4\alpha – sin2\alpha + sin6\alpha – sin4\alpha + \ldots + sin2n\alpha – sin\left( {2n – 2} \right)\alpha $

$ \Leftrightarrow 2sin\alpha \cdot P = sin2n\alpha $

$ \Leftrightarrow P = \frac{{sin2n\alpha }}{{2sin\alpha }}$.

Câu 21: Quỹ đạo của một vật được ném lên từ gốc $O$, với vận tốc ban đầu là $v\left( {\;m/s} \right)$, theo phương hợp với trục hoành $Ox$ một góc $\alpha ,0 < \alpha < \frac{\pi }{2}$, là parabol có phương trình $y = – \frac{g}{{2{v^2}co{s^2}\alpha }}{x^2} + \left( {tan\alpha } \right)x$, trong đó $g$ là gia tốc trọng trường $\left( {g \approx 9,8\;m/{s^2}} \right)$ (giả sử lực cản của không khí không đáng kể). Gọi tầm xa của quỹ đạo là khoảng cách từ $O$ đến giao điểm khác $O$ của quỹ đạo với trục $Ox$ (xem hình vẽ).

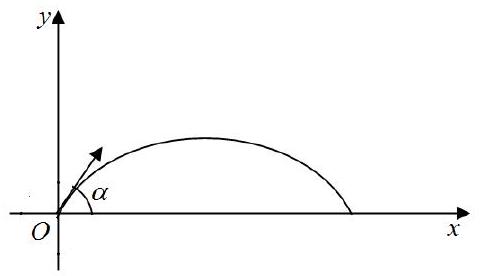
Khi $v$ không đổi, $\alpha $ thay đổi trong khoảng $\left( {0;\frac{\pi }{2}} \right)$, hỏi với giá trị $\alpha $ nào thì tầm xa của quỹ đạo đạt giá trị lớn nhất? Tính giá trị lớn nhất đó $\left( {{x_{max}}} \right)$ theo $v$. Các kết quả lần lượt là:

A. $\alpha = \frac{\pi }{4},{x_{max}} = \frac{{{v^2}}}{g}$.

B. $\alpha = \frac{\pi }{4},{x_{max}} = \frac{{2{v^2}}}{g}$.

C. $\alpha = \frac{\pi }{3},{x_{max}} = \frac{{{v^2}}}{g}$.

D. $\alpha = \frac{\pi }{6},{x_{max}} = \frac{{2{v^2}}}{g}$.

Chọn A

Lời giải

Tầm xa của quỹ đạo thỏa phương trình:

$0 = – \frac{g}{{2{v^2}co{s^2}\alpha }}{x^2} + \left( {tan\alpha } \right)x \Leftrightarrow x = \frac{{{v^2}sin2\alpha }}{g}($ vì $x \ne 0$ ).

Ta có: $x = \frac{{{v^2}sin2\alpha }}{g} \leqslant \frac{{{v^2}}}{g}$. Dấu “=” xảy ra $ \Leftrightarrow sin2\alpha = 1 \Leftrightarrow 2\alpha = \frac{\pi }{2} \Leftrightarrow \alpha = \frac{\pi }{4}$.

Vậy tầm xa của quỹ đạo đạt giá trị lớn nhất khi $\alpha = \frac{\pi }{4}$ và ${x_{max}} = \frac{{{v^2}}}{g}$.

Câu 22: Rút gọn biểu thức: $\frac{{sin2a + sin3a + sin4a}}{{cos2a + cos3a + cos4a}}$.

A. $tan3a$.

B. $tana$.

C. $2tan3a$.

D. $cot3a$.

Chọn A

Lời giải

$\frac{{sin2a + sin3a + sin4a}}{{cos2a + cos3a + cos4a}} = $$ = \frac{{sin2a + sin4a + sin3a}}{{cos2a + cos4a + cos3a}}$

$ = \frac{{2sin3a \cdot cosa + sin3a}}{{2cos3a \cdot cosa + cos3a}} = $$\frac{{sin3a \cdot \left( {2cosa + 1} \right)}}{{cos3a \cdot \left( {2cosa + 1} \right)}} = tan3a.$

Câu 23: Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức $y = 3 – 2\sin x$.

A. $miny = 1;maxy = 4$.

B. $miny = 1;maxy = 5$.

C. $miny = – 1;maxy = 1$.

D. $miny = – 2;maxy = 2$.

Lời giải

Chọn B

Câu 24: Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức $y = co{s^2}x – cosx + 2$.

A. $miny = \frac{7}{4};maxy = 4$.

B. $miny = \frac{7}{4};maxy = 2$.

C. $miny = – 1;maxy = 1$.

D. $miny = \frac{1}{2};maxy = 2$.

Lời giải

Chọn A

Đặt $cosx = t;t \in \left[ { – 1;1} \right]$

Xét hàm số bậc hai: $f\left( t \right) = {t^2} – t + 2$ trên $\left[ { – 1;1} \right]$.

Ta có: $\frac{{ – b}}{{2a}} = \frac{1}{2} \in \left[ { – 1;1} \right]$. Từ đây có bảng biến thiên

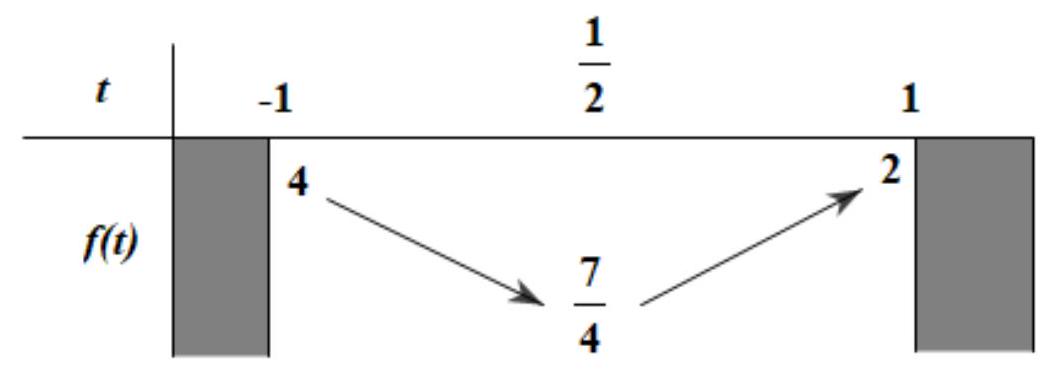
Ta kết luận:

$\min y = \mathop {\min }\limits_{\left[ { – 1;1} \right]} f(t) = \frac{7}{4}$

$\operatorname{m} axy = \mathop {\operatorname{m} ax}\limits_{\left[ { – 1;1} \right]} f(t) = 4$

Câu 25: Khẳng định nào sau đây sai?

A. Hàm số $y = sinx$ đồng biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$.

B. Hàm số $y = cosx$ nghịch biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$.

C. Hàm số $y = tanx$ đồng biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$.

D. Hàm số $y = cotx$ đồng biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$.

Lời giải

Hàm số $y = cotx$ nghịch biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$.

Câu 26: Chọn phát biểu đúng:

A. Các hàm số $y = sinx,y = cosx$ đều là hàm số lẻ.

B. Các hàm số $y = tanx,y = cotx$ đều là hàm số chẵn.

C. Các hàm số $y = tanx,y = cosx$ đều là hàm số chẵn.

D. Các hàm số $y = tanx,y = sinx$ đều là hàm số lẻ.

Lời giải

Hàm số $y = cosx$ là hàm số chẵn nên loại phương án A.

Hàm số $y = sinx,y = tanx,y = cotx$ đều là hàm số lẻ nên loại phương án $B,C$

Phương án D đúng.

Câu 27: Hàm số $y = \sin 2x$ là hàm số tuần hoàn có chu kỳ

A. $T = \pi $.

B. $T = 2\pi $.

C. $T = \frac{\pi }{2}$.

D. $T = \pi $.

Lời giải

Chọn A

Hàm số $y = A\sin \omega x$là hàm số tuần hoàn có chu kỳ $T = \frac{{2\pi }}{{\left| \omega \right|}}$

Do đó, hàm số $y = \sin 2x$là hàm số tuần hoàn có chu kỳ $T = \frac{{2\pi }}{{\left| 2 \right|}} = \pi $

Câu 28: Hàm số $y = \cos \frac{x}{3}$ là hàm số tuần hoàn có chu kỳ

A. $T = \frac{{2\pi }}{3}$.

B. $T = 2\pi $.

C. $T = 6\pi $.

D. $T = \pi $.

Lời giải

Chọn C

Hàm số $y = Acos\omega x$là hàm số tuần hoàn có chu kỳ $T = \frac{{2\pi }}{{\left| \omega \right|}}$

Do đó, hàm số $y = \cos \frac{x}{3}$ là hàm số tuần hoàn có chu kỳ $T = \frac{{2\pi }}{{\left| {\frac{1}{3}} \right|}} = 6\pi $

Câu 29: Người ta nghiên cứu sự sinh trưởng và phát triển của một loại sinh vật $A$ trên một hòn đảo thì thấy được sinh vật $A$ phát triển theo quy luật $s\left( t \right) = a + bsin\frac{{\pi t}}{{18}}$, với $s\left( t \right)$ là số lượng sinh vật $A$ sau $t$ nằm và có đồ thị như hình vẽ dưới. Hỏi số lượng sinh vật $A$ nhiều nhất được bao nhiêu con.:

A. 600 .

B. 650 .

C. 700 .

D. 750 .

Lời giải

Chọn C

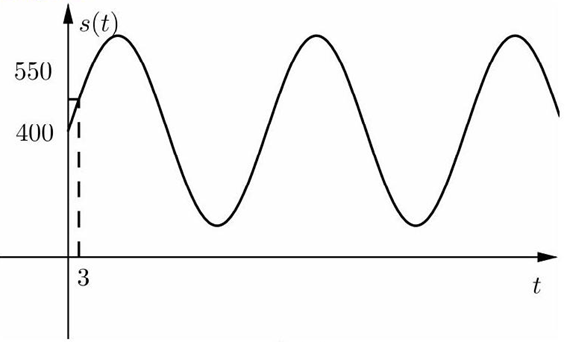
Dựa vào đồ thị ta thấy $\left\{ {\begin{array}{*{20}{l}}
{s\left( 0 \right) = 400} \\
{s\left( 3 \right) = 550}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 400} \\
{b = 550}
\end{array} \Rightarrow s\left( t \right) = 400 + 300sin\frac{\pi }{{18}}t} \right.} \right.$.

Ta có: $100 \leqslant 400 + 300sin\frac{\pi }{{18}}t \leqslant 700\left( {\forall t \geqslant 0} \right)$

Vậy số lượng sinh vật nhiều nhất là 700 con.

Câu 30: Biết các nghiệm của phương trình $cos2x = – \frac{1}{2}$ có dạng $x = \frac{\pi }{m} + k\pi $ và $x = – \frac{\pi }{n} + k\pi ,k \in \mathbb{Z}$; với $m,n$ là các số nguyên dương. Khi đó $m + n$ bằng

A. 4 .

B. 3 .

C. 5 .

D. 6 .

Lời giải

$cos2x = – \frac{1}{2} \Leftrightarrow cos2x = cos\frac{{2\pi }}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x = \frac{{2\pi }}{3} + k2\pi } \\
{2x = – \frac{{2\pi }}{3} + k2\pi }
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{3} + k\pi } \\
{x = – \frac{\pi }{3} + k\pi }
\end{array}\left( {k \in \mathbb{Z}} \right)} \right.} \right.$

$ \Rightarrow m + n = 3 + 3 = 6$.

Câu 31: Phương trình $sin\left( {2x – \frac{\pi }{4}} \right) = sin\left( {x + \frac{{3\pi }}{4}} \right)$ có tổng các nghiệm thuộc khoảng $\left( {0;\pi } \right)$ bằng

A. $\frac{{7\pi }}{2}$.

B. $\pi $.

C. $\frac{{3\pi }}{2}$.

D. $\frac{\pi }{4}$.

Chọn B

Lời giải

Ta có $sin\left( {2x – \frac{\pi }{4}} \right) = sin\left( {x + \frac{{3\pi }}{4}} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x – \frac{\pi }{4} = x + \frac{{3\pi }}{4} + k2\pi } \\
{2x – \frac{\pi }{4} = \frac{\pi }{4} – x + l2\pi }
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pi + k2\pi } \\
{x = \frac{\pi }{6} + l\frac{{2\pi }}{3}}
\end{array}\left( {k,l \in \mathbb{Z}} \right)} \right.} \right.$.

Họ nghiệm $x = \pi + k2\pi $ không có nghiệm nào thuộc khoảng $\left( {0;\pi } \right)$.

$x = \frac{\pi }{6} + l\frac{{2\pi }}{3} \in \left( {0;\pi } \right) \Rightarrow 0 < \frac{\pi }{6} + l\frac{{2\pi }}{3} < \pi \Leftrightarrow l \in \left\{ {0;1} \right\}$.

Vậy phương trình có hai nghiệm thuộc khoảng $\left( {0;\pi } \right)$ là $x = \frac{\pi }{6}$ và $x = \frac{{5\pi }}{6}$. Từ đó suy ra tổng các nghiệm thuộc khoảng $\left( {0;\pi } \right)$ của phương trình này bằng $\pi $.

Câu 32: Giải phương trình $tan3x \cdot cot2x = 1$.

A. $x = k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)$

B. $x = – \frac{\pi }{4} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)$

C. $x = k\pi \left( {k \in \mathbb{Z}} \right)$

D. Vô nghiệm

Chọn D

Lời giải

Điều kiện: $\left\{ {\begin{array}{*{20}{l}}
{cos3x \ne 0} \\
{sin2x \ne 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \ne \frac{\pi }{6} + l\frac{\pi }{3}} \\
{x \ne k\frac{\pi }{2}}
\end{array}\left( {l,k \in \mathbb{Z}} \right)} \right.} \right.$.

$tan3x \cdot cot2x = 1 \Leftrightarrow tan3x = \frac{1}{{cot2x}}$

$ \Leftrightarrow tan3x = tan2x \Leftrightarrow 3x = 2x + k\pi $

$ \Leftrightarrow x = k\pi \left( {k \in \mathbb{Z}} \right)$.

Đối chiếu điều kiện, ta thấy nghiệm $x = k\pi $ không thỏa mãn $x \ne k\frac{\pi }{2}$.

Vậy phương trình đã cho vô nghiệm.

Câu 33: Nghiệm của phương trình $cosx = – \frac{1}{2}$ là:

A. $x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}$.

B. $x = \pm \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}$.

C. $x = \pm \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}$.

D. $x = \pm \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}$.

Chọn A

Lời giải

$cosx = – \frac{1}{2} \Leftrightarrow cosx = cos\frac{{2\pi }}{3} \Leftrightarrow x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}$.

Câu 34: Phương trình $sinx = 1$ có một nghiệm thuộc khoảng $\left( {0;\pi } \right)$ là:

A. $x = \frac{\pi }{4}$.

B. $x = \frac{\pi }{6}$.

C. $x = \frac{\pi }{2}$.

D. $x = \frac{\pi }{3}$.

Lời giải

Chọn C

Ta có $sinx = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \;\left( {k \in \mathbb{Z}} \right)$.

Do đó $x = \frac{\pi }{2}$ là một nghiệm thuộc khoảng $\left( {0;\pi } \right)$ của phương trình $sinx = 1$.

Câu 35: Cho cấp số cộng $\left( {{u_n}} \right)$ với ${u_{10}} = 4;\,{u_{11}} = 12$. Công sai của cấp số cộng đã cho bằng

A. $3$. B. $4$. C. $8$. D. $7$.

Lời giải

Chọn C.

$d = {u_{11}} – {u_{10}} = 12 – 4 = 8$

Câu 36: Cho cấp số cộng $\left( {{u_n}} \right)$ với ${u_{1}} = 3;\,{u_{3}} = -1$. Công sai của cấp số cộng đã cho bằng

A. $-4$. B. $2$. C. $-2$. D. $4$.

Lời giải

Chọn C.

${u_3} = {u_1} + 2d \Rightarrow d = \frac{{{u_3} – {u_1}}}{2} = \frac{{\left( { – 1} \right) – 3}}{2}$

$ \Leftrightarrow d = – 2.$

Câu 37: Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = – 3$, công sai $d = 4$. Tổng 10 số hạng đầu của cấp số cộng bằng

A. $ – 10$. B. $150$. C. $130$. D. $120$.

Lời giải

Chọn B.

${s_n} = \frac{n}{2}\left[ {(2{u_1} + (n – 1)d} \right]$

$ \Rightarrow {S_{10}} = \frac{{10}}{2}\left[ {2( – 3) + (10 – 1).4} \right] = 150$

Câu 38: Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = 2$, công sai $d = – 3$. Tính $M = {u_{10}} + {u_{11}} + {u_{12}} + … + {u_{20}}$.

A. $432$. B. $482$. C. $480$. D. $484$.

Lời giải

Chọn D.

$M = {u_{10}} + {u_{11}} + {u_{12}} + … + {u_{20}} = {S_{20}} – {S_9}$

${S_{20}} = \frac{{20}}{2}\left[ {2.2 + (20 – 1).( – 3)} \right] = 610$

${S_9} = \frac{9}{2}\left[ {2.2 + (9 – 1).( – 3)} \right] = 126$

Vậy $M = 610 – 126 = 484$

Chọn B.

Câu 39: Cho cấp số nhân $\left( {{u_n}} \right)$ với ${u_{10}} = 4;\,{u_{11}} = 12$. Công bội của cấp số nhân đã cho bằng

A. $3$. B. $4$. C. $8$. D. $7$.

Lời giải

Chọn A.

$q = \frac{{{u_{11}}}}{{{u_{10}}}} = \frac{{12}}{4} = 3$

Câu 40: Cho cấp số nhân $\left( {{u_n}} \right)$ với ${u_1} = 3$ và ${u_4} = 24$. Công bội của cấp số nhân đã cho bằng

A. . B. . C. . D. .

Lời giải

Chọn B.

${u_n} = {u_1}.{q^{n – 1}}$

${u_4} = {u_1}.{q^3} \Rightarrow {q^3} = \frac{{{u_4}}}{{{u_1}}} = \frac{{24}}{3} = 8$

$ \Rightarrow q = 2.$

Câu 41: Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = 2$, công bội $q = – 3$. Tổng 10 số hạng đầu của cấp số nhân bằng

A. $ – 29524$. B. $ – 29574$. C. $ – 29525$. D. $ – 29528$.

Lời giải

Chọn A.

${s_n} = {u_1}.\frac{{1 – {q^n}}}{{1 – q}}$

$ \Rightarrow {S_{10}} = 2.\frac{{1 – {{( – 3)}^{10}}}}{{1 – ( – 3)}} = – 29524$

Câu 42: Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = 2$, công bội $q = – \frac{1}{2}$. Tính $M = {u_5} + {u_6} + {u_7} + … + {u_{11}}$.

A. $\frac{4}{5}$. B. $\frac{{49}}{{512}}$. C. $\frac{{47}}{{512}}$. D. $\frac{{43}}{{512}}$.

Lời giải

Chọn B.

$M = {u_5} + {u_6} + {u_7} + … + {u_{11}} = {S_{11}} – {S_4}$

${S_{11}} = {u_1}.\frac{{1 – {q^{11}}}}{{1 – q}} = 2.\frac{{1 – {{\left( { – \frac{1}{2}} \right)}^{11}}}}{{1 – \left( { – \frac{1}{2}} \right)}} = \frac{{683}}{{512}}$

${S_4} = {u_1}.\frac{{1 – {q^4}}}{{1 – q}} = 2.\frac{{1 – {{\left( { – \frac{1}{2}} \right)}^4}}}{{1 – \left( { – \frac{1}{2}} \right)}} = \frac{5}{4}$

Vậy $M = {S_{11}} – {S_4} = \frac{{683}}{{512}} – \frac{5}{4} = \frac{{43}}{{512}}$

Câu 43: Trong các khẳng định sau, khẳng định nào đúng?

A. Nếu 3 điểm $A,B,C$ là 3 điểm chung của 2 mặt phẳng $\left( P \right)$ và $\left( Q \right)$ thì $A,B,C$ thẳng hàng.

B. Nếu $A,B,C$ thẳng hàng và $\left( P \right),\left( Q \right)$ có điểm chung là $A$ thì $B,C$ cũng là 2 điểm chung của $\left( P \right)$ và $\left( Q \right)$.

C. Nếu 3 điểm $A,B,C$ là 3 điểm chung của 2 mặt phẳng $\left( P \right)$ và $\left( Q \right)$ phân biệt thì $A,B,C$ không thẳng hàng.

D. Nếu $A,B,C$ thẳng hàng và $A,B$ là 2 điểm chung của $\left( P \right)$ và $\left( Q \right)$ thì $C$ cũng là điểm chung của $\left( P \right)$ và $\left( Q \right)$.

Chọn D

Lời giải

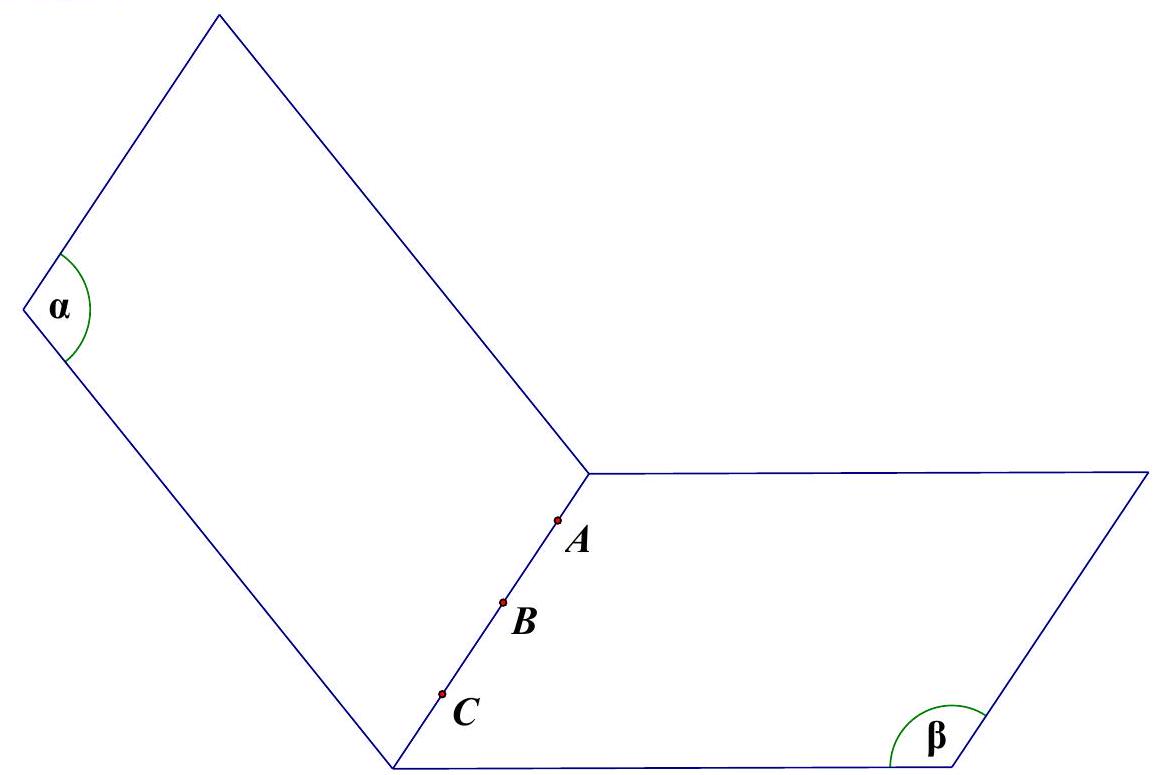
• A sai. Nếu $\left( P \right)$ và $\left( Q \right)$ trùng nhau thì 2 mặt phẳng có vô số điểm chung. Khi đó, chưa đủ điều kiện để kết luận $A,B,C$ thẳng hàng.

• $B$ sai. Có vô số đường thẳng đi qua $A$, khi đó $B,C$ chưa chắc đã thuộc giao tuyến của $\left( P \right)$ và $\left( Q \right)$.

• $C$ sai. Hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ phân biệt giao nhau tại 1 giao tuyến duy nhất, nếu 3 điểm $A,B,C$ là 3 điểm chung của 2 mặt phẳng thì $A,B,C$ cùng thuộc giao tuyến.

Câu 44: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M,N,Q$ lần lượt là trung điểm của các cạnh $AB,AD,SC$. Thiết diện của hình chóp với mặt phẳng $\left( {MNQ} \right)$ là đa giác có bao nhiêu cạnh ?

A. 3 .

B. 4 .

C. 5 .

D. 6 .

Chọn C

Lời giải

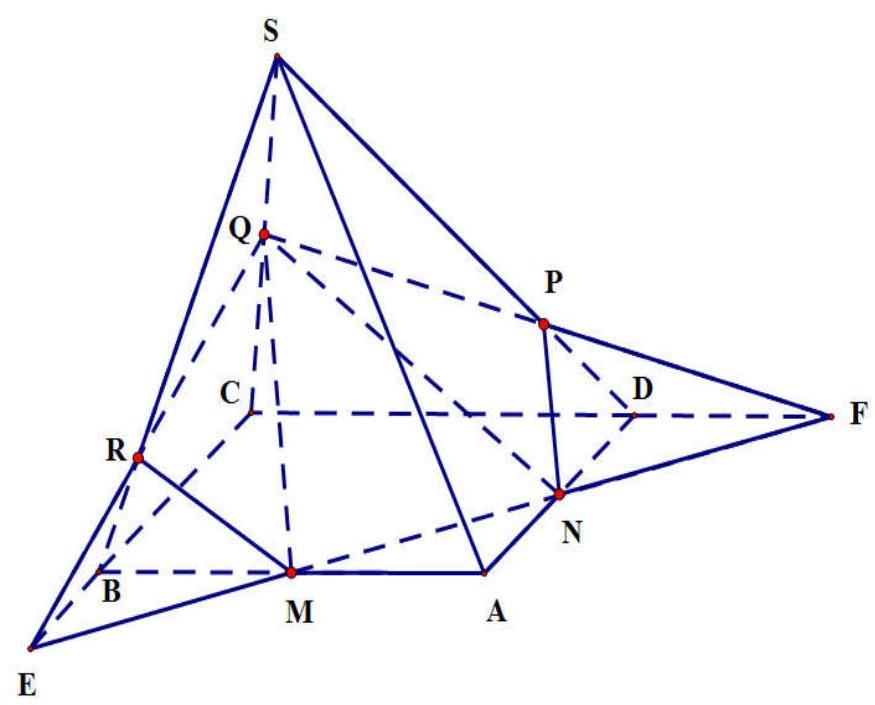
Thiết diện của hình chóp với mặt phẳng $\left( {MNQ} \right)$ là ngũ giác $MNPQR$. Đa giác này có 5 cạnh.

Câu 45: Cho hình chóp tứ giác $S \cdot ABCD$ với đáy $ABCD$ có các cạnh đối diện không song song với nhau.

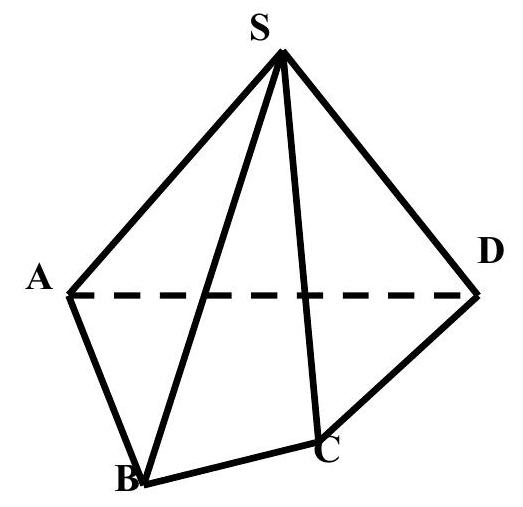
Giao điểm của $BC$ và mặt phẳng $\left( {SAD} \right)$ là

A. Điểm $H$, trong đó $H = AB \cap CD$.

B. Điểm $K$, trong đó $K = AD \cap BC$.

C. Giao điểm của $BC$ và $SD$.

D. Giao điểm của $BC$ và $SA$.

Lời giải

Xét mặt phẳng $\left( {ABCD} \right)$ kéo dài $BC$ cắt $AD$ tại $K$

Câu 46: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là một hình bình hành tâm $O$. Gọi $M,N,P$ là ba điểm trên các cạnh $AD,CD,SO$. Thiết diện của hình chóp với mặt phẳng $\left( {MNP} \right)$ là hình gì?

A. Ngũ giác.

B. Tứ giác.

C. Hình thang.

D. Hình bình hành.

Chọn A

Lời giải

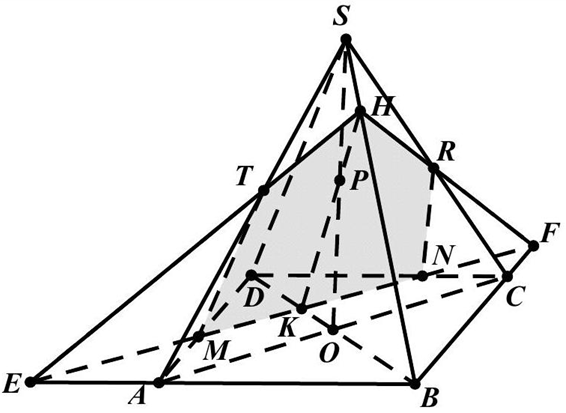
Trong mặt phẳng $\left( {ABCD} \right)$ gọi $E,K,F$ lần lượt là giao điểm của $MN$ với $BA,BD,BC$.

Trong mặt phẳng $\left( {SDB} \right)$ gọi $H = KP \cap SB$

Trong mặt phẳng $\left( {SAB} \right)$ gọi $T = EH \cap SA$

Trong mặt phẳng $\left( {SBC} \right)$ gọi $R = FH \cap SC$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{E \in MN} \\
{H \in KP}
\end{array} \Rightarrow EH \subset \left( {MNP} \right),\left\{ {\begin{array}{*{20}{l}}
{T \in SA} \\
{T \in EH \subset \left( {MNP} \right)}
\end{array} \Rightarrow T = SA \cap \left( {MNP} \right)} \right.} \right.$.

Lí luận tương tự ta có $R = SC \cap \left( {MNP} \right)$.

Thiết diện là ngũ giác $MNRHT$.

Câu 47: Cho hình chóp $S.ABCD$ có đáy là hình bình hành $ABCD$. Giao tuyến của hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SBC} \right)$ là đường thẳng song song với đường thẳng nào sau đây?

A. $AC$.

B. $BD$.

C. $AD$.

D. $SC$.

Chọn C

Lời giải

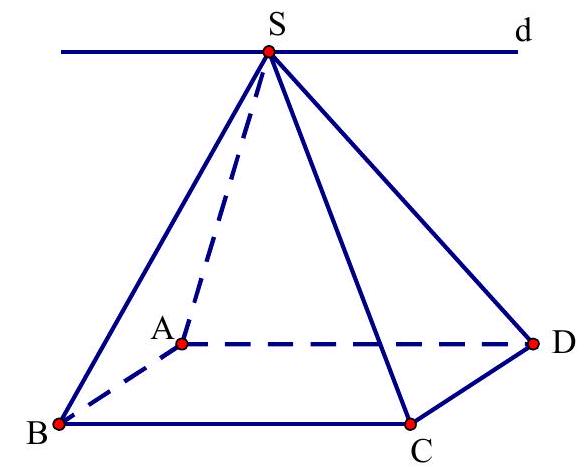
$\left( {SAD} \right)$ chứa $AD,\left( {SBC} \right)$ chứa $BC$ và $AD//BC$.

$\left( {SAD} \right)$ và $\left( {SBC} \right)$ có điểm $S$ là điểm chung.

Suy ra giao tuyến của $\left( {SAD} \right)$ và $\left( {SBC} \right)$ là đường thẳng $d$ đi qua điểm $S$ và $d//AD$.

Câu 48: Cho hình chóp $S.ABCD$ có $AD$ cắt $BC$ tại $E$. Gọi $M$ là trung điểm của $SA,N$ là giao điểm của $SD$ và $\left( {BCM} \right)$. Khẳng định nào sau đây đúng?

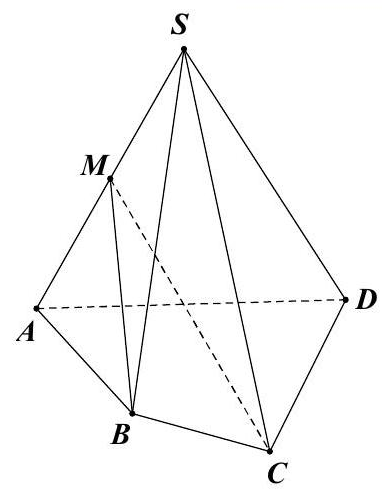
A. $AD,BN,CM$ đồng quy.

C. $AD.BC,MN$ đồng quy.

B. $AC,BD,CM$ đồng quy.

D. $AC,BD,BN$ đồng quy.

Chọn C

Lời giải

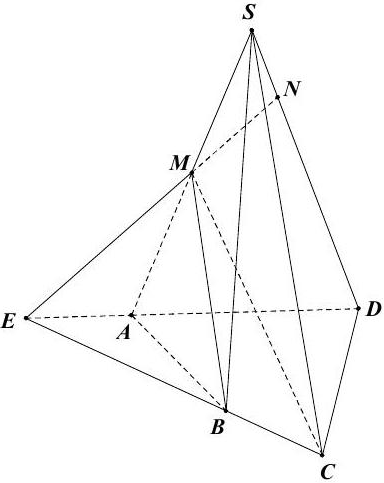
Từ giả thiết ta có $MN$ là giao tuyến của $\left( {BCM} \right)$ và $\left( {SAD} \right)$.

Ba mặt phẳng $\left( {BCM} \right),\left( {SAD} \right)$ và $\left( {ABCD} \right)$ đôi một cắt nhau theo ba giao tuyến phân biệt là $MN,AD$ và $BC$.

Mặt khác $AD$ cắt $BC$ tại $E$, do đó $MN,AD$ và $BC$ đồng quy tại $E$.

Câu 49: Trong mặt phẳng $\left( P \right)$ cho hai đường thẳng $a$ và $b$. Khẳng định nào sau đây là sai về vị trí tương đối của $a$ và $b$.

A. $a,b$ có thể cắt nhau.

B. $a,b$ có thể song song.

C. $a,b$ có thể trùng nhau.

D. $a,b$ có thể chéo nhau.

Chọn D

Lời giải

Do hai đường thẳng $a$ và $b$ là đồng phẳng nên chúng chỉ có thể hoặc cắt nhau, hoặc song song, hoặc trùng nhau.

Câu 50: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang với các cạnh đáy là $AB$ và $CD$. Gọi $I,J$ lần lượt là trung điểm của các cạnh $AD$ và $BC$ và $G$ là trọng tâm của tam giác $SAB$. Tìm điều kiện của $AB$ và $CD$ để thiết diện của $\left( {IJG} \right)$ và hình chóp là một hình bình hành.

A. $AB = \frac{2}{3}CD$.

B. $AB = CD$.

C. $AB = \frac{3}{2}CD$.

D. $AB = 3CD$.

Chọn D

Lời giải

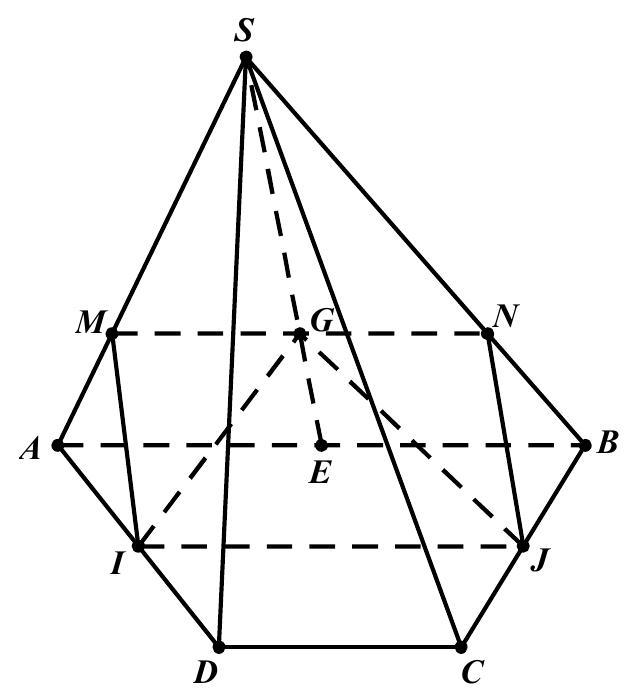
Ta có $ABCD$ là hình thang và $I,J$ là trung điểm của $AD,BC$ nên $IJ//AB$.

Do $\left\{ {\begin{array}{*{20}{l}}
{G \in \left( {SAB} \right) \cap \left( {IJG} \right)} \\
{AB \subset \left( {SAB} \right)} \\
{IJ \subset \left( {IJG} \right)} \\
{AB//IJ}
\end{array} \Rightarrow \left( {SAB} \right) \cap \left( {IJG} \right) = MN//IJ//AB} \right.$ với $M \in SA,N \in SB$.

Vậy thiết diện của $\left( {IJG} \right)$ và hình chóp là tứ giác $MNJI$.

Do $G$ là trọng tâm tam giác $SAB$ và $MN//AB$ nên $\frac{{MN}}{{AB}} = \frac{{SG}}{{SE}} = \frac{2}{3}$

( $E$ là trung điểm của $AB) \Rightarrow MN = \frac{2}{3}AB$.

Lại có $IJ = \frac{1}{2}\left( {AB + CD} \right)$. Vì $MN//IJ$ nên $MNIJ$ là hình thang, do đó $MNIJ$ là hình bình hành khi $MN = IJ$

$ \Leftrightarrow \frac{2}{3}AB = \frac{1}{2}\left( {AB + CD} \right) \Leftrightarrow AB = 3CD$.

Vậy thiết diện là hình bình hành khi $AB = 3CD$.

Câu 51: Cho hình chóp $S.ABCD$. Gọi $G,E$ lần lượt là trọng tâm của các tam giác $SAB$ và $SCD$. Gọi $M,N$ lần lượt là trung điểm các cạnh $AB$ và $CD$. Mệnh đề nào dưới đây là mệnh đề đúng?

A. $MN$ và $GE$ trùng nhau.

B. $MN$ và $GE$ chéo nhau.

C. $MN$ và $GE$ song song với nhau.

D. $MN$ và $GE$ cắt nhau.

Chọn C

Lời giải

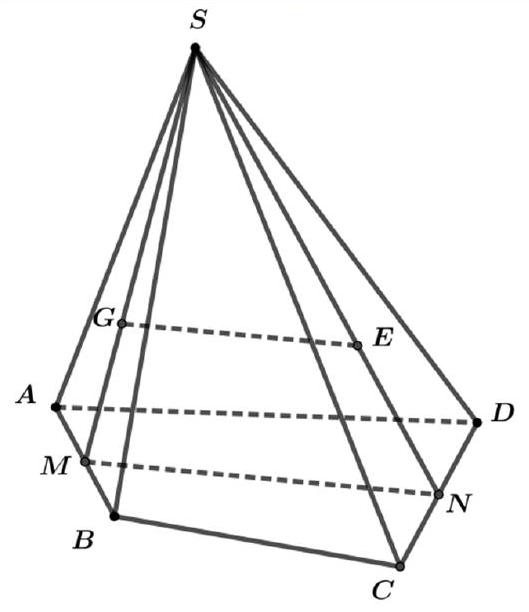
Xét tam giác $SMN$ ta có: $\frac{{SG}}{{SM}} = \frac{{SE}}{{SN}} = \frac{2}{3} \Rightarrow GE//MN$.

Câu 52: Cho hình chóp $S.ABCD$ với đáy $ABCD$ có các cặp cạnh đối cắt nhau. Gọi $O,E,F$ lần lượt là giao điểm của các cặp đường thẳng $AC$ và $BD,AD$ và $BC,AB$ và $CD$. Mặt phẳng $\left( P \right)$ cắt các cạnh $SA,SB,SC,SD$ lần lượt tại các điểm $M,N,P$ và $Q$. Gọi $G$ là giao điểm của $MP$ và $NQ$. Bộ ba điểm nào sau đây thẳng hàng?

A. $G,S$ và $F$.

B. $G,S$ và $O$.

C. $G,S$ và $E$.

D. $G,A$ và $C$.

Chọn B

Lời giải

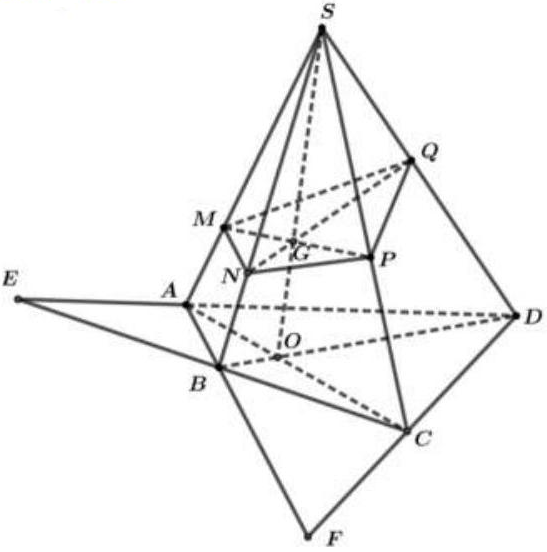
Ta có: $S \in \left( {SAC} \right) \cap \left( {SBD} \right)$ (1)

Vì $\left\{ O \right\} = AC \cap BD$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{O \in AC \subset \left( {SAC} \right)} \\
{O \in BD \subset \left( {SBD} \right)}
\end{array} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right)} \right.$

Vì $\left\{ G \right\} = MP \cap NQ$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{G \in MP \subset \left( {SAC} \right)} \\
{G \in NQ \subset \left( {SBD} \right)}
\end{array} \Rightarrow G \in \left( {SAC} \right) \cap \left( {SBD} \right)} \right.$

Từ (1), (2), (3) suy ra $G,S$ và $O$ thẳng hàng.

Câu 53: Nếu đường thẳng $d$ không nằm trong mặt phẳng $\left( \alpha \right)$ và $d$ song song với đường thẳng $d’$ nằm trong $\left( \alpha \right)$ thì

A. $d$ và $\left( \alpha \right)$ có một điểm chung duy nhất.

B. $d$ và $\left( \alpha \right)$ có ít nhất hai điểm chung.

C. $d’$ song song với $\left( \alpha \right)$.

D. $d$ song song với $\left( \alpha \right)$.

Lời giải

Chọn D

Theo định lý ta có: “Nếu đường thăng $d$ không nằm trong mặt phẳng $\left( \alpha \right)$ và d song song với đưòng thẳng d’ nằm trong $\left( \alpha \right)$ thì $d$ song song với $\left( \alpha \right)$ “.

Câu 54: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang $\left( {AB//CD} \right)$. Mặt phẳng $\left( Q \right)$ qua $D$ và song song với $SA,AB$. Giao tuyến của $\left( Q \right)$ và $\left( {ABCD} \right)$ là

A. $SD$.

B. $BD$.

C. $AC$.

D. $CD$.

Chọn D

Lời giải

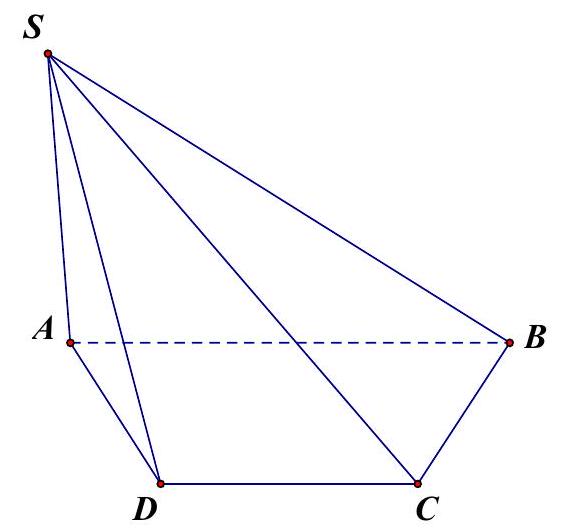
Ta có $\left\{ {\begin{array}{*{20}{l}}
{AB//\left( Q \right)} \\
{AB \subset \left( {ABCD} \right)} \\
{D \in \left( Q \right) \cap \left( {ABCD} \right)}
\end{array} \Rightarrow \left( Q \right) \cap \left( {ABCD} \right) = CD//AB} \right.$

Câu 55: Cho hình chóp $S \cdot ABCD$ có đáy là hình bình hành và $O$ là giao điểm hai đường chéo. Gọi $M,N$ lần lượt là trung điểm của $SD$ và $CD$. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {OMN} \right)$.

A. Hình thang $MNEF$ với $E,F$ lần lượt là trung điểm của $AB,SA$.

B. Tam giác $OMN$.

C. Hình bình hành $MNEF$ với $E,F$ lần lượt là trung điểm của $AB,SA$.

D. Tứ giác $AMNO$.

Chọn A

Lời giải

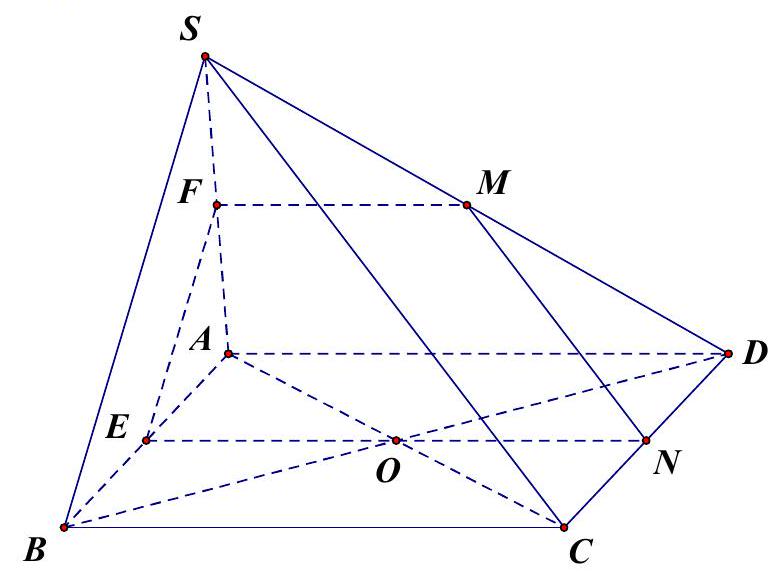
• $\left( {OMN} \right) \cap \left( {SCD} \right) = MN$.

$*\left( {OMN} \right) \cap \left( {ABCD} \right) = ON$. Trong $\left( {ABCD} \right)$ gọi $E$ là giao của $ON$ và $AB$ suy ra $E$ là trung điểm $AB$.

• Ta có $\left\{ {\begin{array}{*{20}{l}}
{ON//AD} \\
{ON \subset \left( {OMN} \right)} \\
{AD \subset \left( {SAD} \right)} \\
{M \in \left( {OMN} \right) \cap \left( {SAD} \right)}
\end{array} \Rightarrow \left( {OMN} \right) \cap \left( {SAD} \right) = Mx//ON//AD} \right.$.

Trong $\left( {SAD} \right)$ gọi $F$ là giao của $Mx$ và $SA$.

Suy ra thiết diện là hình thang $MNEF\left( {MF//NE} \right)$.

Câu 56: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang $\left( {AB//CD,AB = 2CD} \right)$. Gọi $G$ là trọng tâm của tam giác $SAD$. Mặt phẳng $\left( P \right)$ qua $CG$ và song song $AB$ cắt hình chóp theo thiết diện là hình gì?

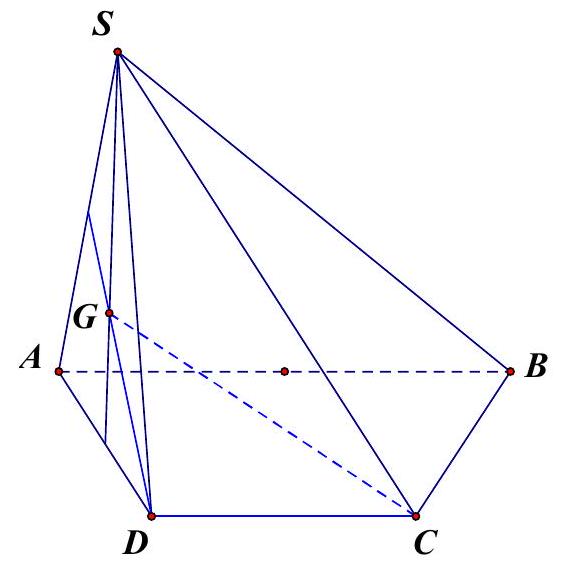
A. Tam giác cân.

B. Ngũ giác.

C. Hình vuông.

D. Hình bình hành.

Lời giải

Chọn D

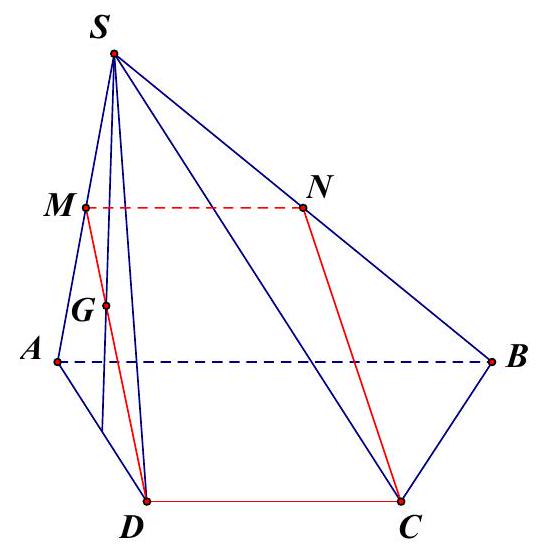
$\left\{ {\begin{array}{*{20}{l}}
{AB//\left( P \right)} \\
{AB \subset \left( {ABCD} \right)} \\
{C \in \left( P \right) \cap \left( {ABCD} \right)}
\end{array} \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = CD//AB} \right.$

• Trong $\left( {SAD} \right):DG$ cắt $SA$ tại $M$ là trung điểm của $SA$.

$*\left\{ {\begin{array}{*{20}{l}}
{AB//\left( P \right)} \\
{AB \subset \left( {SAB} \right)} \\
{M \in \left( P \right) \cap \left( {SAB} \right)}
\end{array} \Rightarrow \left( P \right) \cap \left( {SAB} \right) = Mx//AB} \right.$

Trong $\left( {SAB} \right)$ gọi $N$ là giao của $Mx$ và $SB$ thì $M$ là trung điểm $SB$ và $MN = \frac{1}{2}AB = CD$ Vậy thiết diện là hình bình hành $CDMN$.

Câu 57: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Trên các cạnh $SA,SB,AD$ lần lượt lấy các điểm $M,N,K$ sao cho $\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{{DK}}{{DA}}$. Khẳng định nào sau đây là sai?

A. $MN//\left( {ABCD} \right)$

B. $SD//\left( {MNK} \right)$.

C. $NK//\left( {SCD} \right)$.

D. $SC$ không song song $\left( {MNK} \right)$.

Lời giải

Chọn D

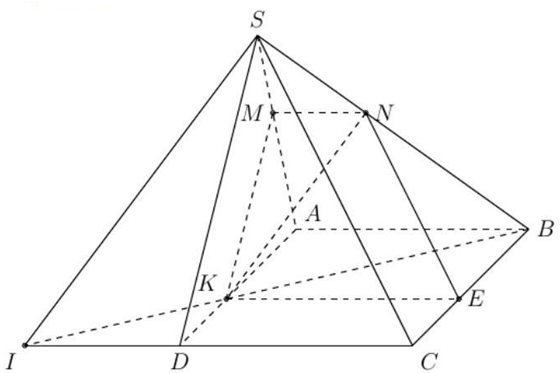
• Tam giác $SAB$ có $\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} \Rightarrow MN//AB$.

Mà $MN \not\subset \left( {ABCD} \right),AB \subset \left( {ABCD} \right) \Rightarrow MN//\left( {ABCD} \right)$

• Tam giác $SAD$ có $\frac{{SM}}{{SA}} = \frac{{DK}}{{DA}} \Rightarrow SD//MK$.

Mà $SD \not\subset \left( {MNK} \right),MK \subset \left( {MNK} \right) \Rightarrow SD//\left( {MNK} \right)$

Trong mặt phẳng $\left( {ABCD} \right)$, gọi $I$ là giao điểm của $BK$ và $CD$.

• Tam giác $IBC$ có $DK//BC \Rightarrow \frac{{IK}}{{IB}} = \frac{{DK}}{{BC}} = \frac{{DK}}{{DA}}$

Theo giả thiết ta có $\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{{DK}}{{DA}} \Rightarrow \frac{{IK}}{{IB}} = \frac{{SN}}{{SB}} \Rightarrow NK//SI$.

Mà $NK \not\subset \left( {SCD} \right),SI \subset \left( {SCD} \right) \Rightarrow NK//\left( {SCD} \right)$.

• Qua $K$ kẻ đường thẳng $\Delta //CD$ cắt $CB$ tại $E$.

Theo giả thiết ta có $\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} \Rightarrow MN//AB$ mà $AB//CD$

Suy ra: $MN//AB//KE$ hay $E \in \left( {MNK} \right)$.

Ta có: $\frac{{SN}}{{SB}} = \frac{{DK}}{{DA}}$ mà $\frac{{CE}}{{CB}} = \frac{{DK}}{{DA}} \Rightarrow \frac{{SN}}{{SB}} = \frac{{CE}}{{CB}} \Rightarrow NE//SC$.

Mà $SC \not\subset \left( {MNK} \right),NE \subset \left( {MNK} \right) \Rightarrow SC//\left( {MNK} \right)$.

Vậy khẳng định $SC$ không song song $\left( {MNK} \right)$ là sai.

PHẦN 2. TỰ LUẬN

Câu 58: Cho $tanx = 2$. Tính giá trị của biểu thức sau: $A = \frac{{si{n^3}x + 2co{s^3}x}}{{2sinx + 3cosx}}$.

Lời giải

Vì $tanx$ xác định nên $cosx \ne 0$. Chia tử và mẫu của phân thức cho luỹ thừa thích hợp của $cosx$ để biểu diễn biểu thức theo $tanx$.

Ta có: $A = \frac{{\frac{{si{n^3}x}}{{co{s^3}x}} + 2}}{{\left( {2\frac{{sinx}}{{cosx}} + 3} \right) \cdot \frac{1}{{co{s^2}x}}}} = \frac{{ta{n^3}x + 2}}{{\left( {2tanx + 3} \right)\left( {ta{n^2}x + 1} \right)}}$

$ = \frac{{{2^3} + 2}}{{\left( {2.2 + 3} \right)\left( {{2^2} + 1} \right)}} = \frac{2}{7}$

Câu 59: Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 14). Nghiên cứu trò chơi này, người ta thấy khoảng cách $h\left( m \right)$ từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian $t(s$ ) (với $t \geqslant 0$ ) bởi hệ thức $h = \left| d \right|$ với $d = 3cos\left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]$, trong đó ta quy ước $d > 0$ khi vị trí cân bằng ở phía sau lưng người chơi đu và $d < 0$ trong trường hợp ngược lại. Vào thời gian $t$ nào thì khoảng cách $h$ là $3m;0m$ ?

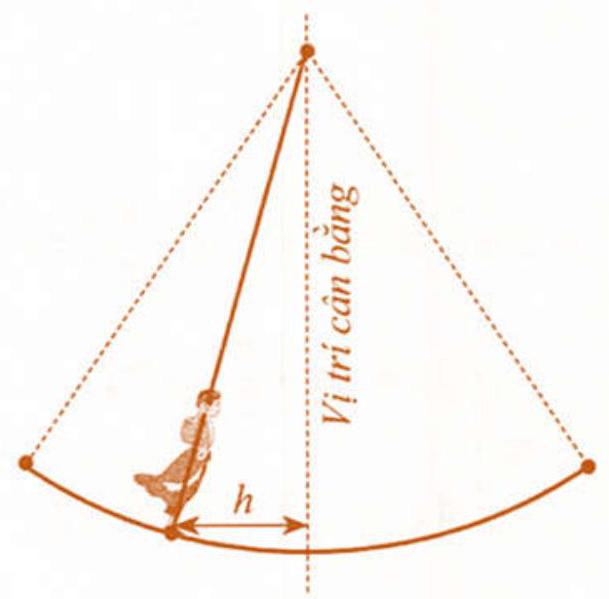
Hình 14

Lời giải

Do $ – 1 \leqslant cos\left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] \leqslant 1$ nên $ – 3 \leqslant 3cos\left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] \leqslant 3$ hay $ – 3 \leqslant d \leqslant 3$.

Do đó, $0 \leqslant \left| d \right| \leqslant 3$.

Vậy $\;h = 3\;$ khi $\;\left| d \right| = 3\;$ hay $\;cos\left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \pm 1 \Leftrightarrow sin\left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0$

$ \Leftrightarrow \frac{\pi }{3}\left( {2t – 1} \right) = k\pi \Leftrightarrow t = \frac{{1 + 3k}}{2}\;$ với $\;k \in \mathbb{Z},k \geqslant 0;h = 0\;$ khi $\;\left| d \right| = 0\;$ hay

$cos\left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0 \Leftrightarrow \frac{\pi }{3}\left( {2t – 1} \right) = \frac{\pi }{2} + k\pi $

$ \Leftrightarrow t = \frac{{5 + 6k}}{4}$ với $k \in \mathbb{Z},k \geqslant 0$.

Câu 60: Cho hình chóp tứ giác $S \cdot ABCD$ có đáy không là hình thang. Gọi $O$ là giao điểm của $AC$ và $BD$. Trên $SO$ lấy điểm $I$ sao cho $SI = 2IO$.

a) Xác định các giao điểm $M,N$ lần lượt của $SA,SD$ với mặt phẳng $\left( {IBC} \right)$.

$\left. {{b^*}} \right)$ Chứng minh rằng các đường thẳng $AD,BC$ và $MN$ đồng quy.

Lời giải

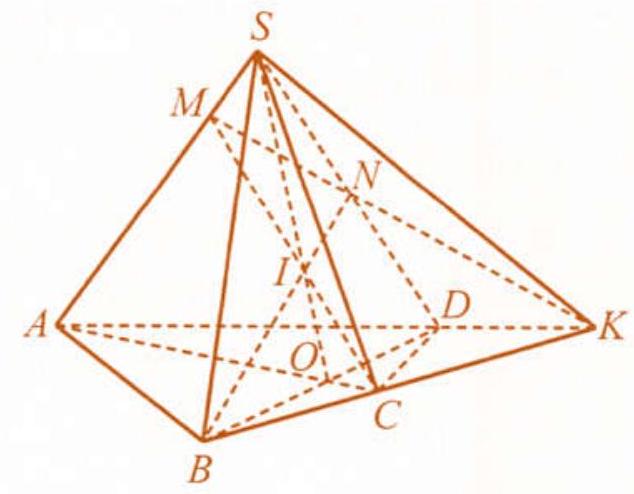
Hình 50

a) Trong mặt phẳng $\left( {SAC} \right)$, gọi $M$ là giao điểm của $CI$ và $SA$. Vì $M \in CI$ nên $M \in \left( {IBC} \right)$. Vậy $M$ là giao điểm của $SA$ với mặt phẳng $\left( {IBC} \right)$. Tương tự, trong mặt phẳng $\left( {SBD} \right)$, gọi $N$ là giao điểm của $BI$ với $SD$, khi đó, $N$ là giao điểm của $SD$ với mặt phẳng $\left( {IBC} \right)$.

b*) Do $ABCD$ không là hình thang nên $AD$ cắt $BC$ tại $K$. Ta có $K \in BC \subset \left( {IBC} \right)$, $K \in AD \subset \left( {SAD} \right)$ nên $K$ là một điểm chung của $\left( {IBC} \right)$ và $\left( {SAD} \right)$.

Mà $MN = \left( {IBC} \right) \cap \left( {SAD} \right)$ nên $K \in MN$. Vậy các đường thẳng $AD,BC$ và $MN$ cùng đi qua điểm $K$.

Câu 61: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$ là điểm chuyển động trên cạnh $SC(M$ khác $C),\left( P \right)$ là mặt phẳng chứa đường thẳng $AM$ và song song với $BD$. Chứng minh rằng mặt phẳng $\left( P \right)$ luôn đi qua một đường thẳng cố định khi điểm $M$ chuyển động trên cạnh $SC$.

Lời giải

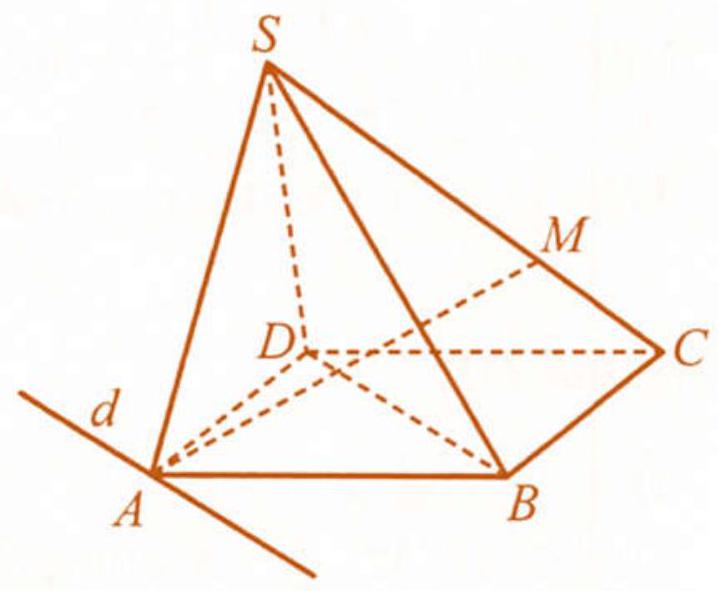
Hình 57

Mặt phẳng $\left( P \right)$ chứa đường thẳng $AM$ và song song với $BD$ nên $\left( P \right)$ cắt $\left( {ABCD} \right)$ theo giao tuyến $d$ đi qua $A$ và song song với $BD$. Vì hình bình hành $ABCD$ cố định nên đường thẳng $d$ cố định trong $\left( {ABCD} \right)$.

Vậy khi $M$ chuyển động trên cạnh $SC$ thì mặt phẳng $\left( P \right)$ luôn luôn đi qua đường thẳng $d$ cố định.