Bài Tập Tự Luận Ôn Chương Quan Hệ Song Song Trong Không Gian Giải Chi Tiết

Bài tập tự luận ôn chương quan hệ song song trong không gian giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.

Câu 1. Cho hình chóp S.ABCD, có đáy ABCD là tứ giác có cặp cạnh đối không song song, điểm M thuộc cạnh SA. Tìm giao tuyến của các cặp mặt phẳng sau:

a) $\left( {SAC} \right)$ và $\left( {SBD} \right).$ b) $\left( {SAC} \right)$ và $\left( {MBD} \right).$

c) $\left( {MBC} \right)$ và $\left( {SAD} \right).$ d) $\left( {SAB} \right)$ và $\left( {SCD} \right).$

Lời giải

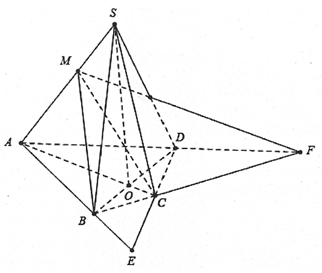
a) Trong mặt phẳng $\left( {ABCD} \right)$ gọi $O = AC \cap BD \Rightarrow \left\{ \begin{gathered}
O \in AC \subset \left( {SAC} \right) \hfill \\
O \in BD \subset \left( {SBD} \right) \hfill \\
\end{gathered} \right..$

khi đó hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBD} \right)$ có hai điểm chung là S và O $ \Rightarrow SO = \left( {SAC} \right) \cap \left( {SBD} \right).$

b) Điểm $M \in SA \Rightarrow M \in \left( {SAC} \right).$

Hai mặt phẳng $\left( {SAC} \right)$ và $\left( {MBD} \right)$ có hai điểm chung là O và M nên $OM = \left( {SAC} \right) \cap \left( {MBD} \right).$

c) Gọi $F = AD \cap BC$ suy ra $\left\{ \begin{gathered}
F \in \left( {MBC} \right) \hfill \\
F \in \left( {SAD} \right) \hfill \\
\end{gathered} \right..$ Khi đó hai mặt phẳng $\left( {MBC} \right)$ và $\left( {SAD} \right)$ có hai điểm chung là M và F $ \Rightarrow MF = \left( {MBC} \right) \cap \left( {SAD} \right).$

d) Gọi $E = AB \cap CD$ suy ra $\left\{ \begin{gathered}
E \in \left( {SAB} \right) \hfill \\
E \in \left( {SCD} \right) \hfill \\
\end{gathered} \right. \Rightarrow $ hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ có hai điểm chung là S và E$ \Rightarrow SE = \left( {SAB} \right) \cap \left( {SCD} \right).$

Câu 2. Cho hình chóp S.ABC và điểm I thuộc đoạn SA. Một đường thẳng không song song với AC cắt các cạnh AB và BC lần lượt tại J và K. Tìm giao tuyến của các cặp mặt phẳng sau:

a) Mặt phẳng $\left( {IJK} \right)$ và $\left( {SAC} \right).$

b) Mặt phẳng $\left( {IJK} \right)$ và $\left( {SAB} \right).$

c) Mặt phẳng $\left( {IJK} \right)$ và $\left( {SBC} \right).$

Lời giải

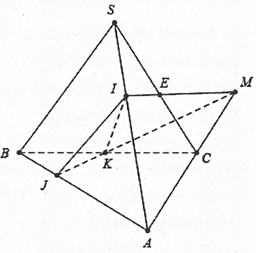
a) Trong mặt phẳng $\left( {ABC} \right)$ gọi $M = JK \cap AC.$

Khi đó 2 mặt phẳng $\left( {IJK} \right)$ và $\left( {SAC} \right)$ có hai điểm chung là I và M.

Suy ra $IM = \left( {IJK} \right) \cap \left( {SAC} \right).$

b) Hai mặt phẳng $\left( {IJK} \right)$ và $\left( {SAB} \right)$ có hai điểm chung là I và $J \Rightarrow IJ = \left( {IJK} \right) \cap \left( {SAB} \right).$

c) Trong mặt phẳng $\left( {SAC} \right)$ gọi $E = SC \cap IM$

Khi đó $\left\{ \begin{gathered}
E \in \left( {IJK} \right) \hfill \\
E \in \left( {SBC} \right) \hfill \\
\end{gathered} \right. \Rightarrow $ hai mặt phẳng $\left( {IJK} \right)$ và $\left( {SBC} \right)$ có hai điểm chung là E và K.

Do đó $KE = \left( {IJK} \right) \cap \left( {SBC} \right).$

Câu 3. Cho hình chóp $S.ABCD$, có đáy là hình thang với đáy lớn $AB$. Gọi $M,N$ lần lượt là trung điểm của $SA$ và $SB$.

a) Chứng minh: $MN\,//\,CD$

b) Tìm giao điểm $P$ của $SC$ với $\left( {AND} \right)$. Kéo dài $AN$ và $DP$ cắt nhau tại $I$ .

Chứng minh $SI//AB//CD$. Tứ giác $SIBA$ là hình gì? Vì sao?

Lời giải

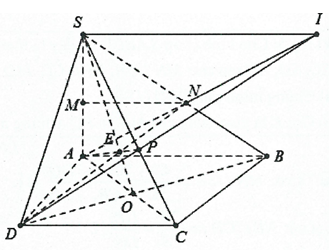
a) Ta có $MN$ là đường trung bình của tam giác $SAB$ nên $MN//AB$ mặt khác $AB//CD \Rightarrow MN//CD$.

b) Gọi $O = AC \cap CD$ và $E = SO \cap ND$ khi đó $SE$ cắt $SC$ tại $P$.

Xét 3 mặt phẳng $\left( {SAB} \right);\,\left( {SCD} \right)$ và $\left( {ABCD} \right)$ có các giao tuyến chung là $SI,\,AB$ và $CD$ song song hoặc đồng quy.

Do $AB//CD$ nên $SI//AB//CD$.

Ta có: $SI//AB \Rightarrow \frac{{NS}}{{NB}} = \frac{{NI}}{{NA}} = \frac{{SI}}{{AB}} = 1$

Khi đó: $\left\{ \begin{gathered}
SI//AB \hfill \\
SI = AB \hfill \\
\end{gathered} \right. \Rightarrow SIBA$ là hình bình hành.

Câu 4. Cho tứ diện $ABCD$. Gọi $M,N,P,Q,R,S$ lần lượt là trung điểm của $AB,CD,BC,AD,AC,BD$.

a) Chứng minh $MNPQ$ là hình bình hành.

b) Từ đó suy ra ba đoạn $MN,PQ,RS$ cắt nhau tại trung điểm của mỗi đoạn.

Lời giải

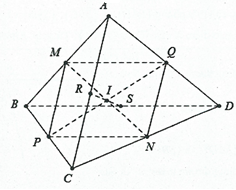
a) Vì $MQ$ là đường trung bình của tam giác $ABD$ nên ta có $\left\{ \begin{gathered}
MQ//BD \hfill \\
MQ = \frac{1}{2}BD \hfill \\
\end{gathered} \right.$

Tương tự ta cũng có: $\left\{ \begin{gathered}
NP//BD \hfill \\
NP = \frac{1}{2}BD \hfill \\
\end{gathered} \right.$

Do vậy $MQNP$ là hình bình hành từ đó suy ra $MN$ và $PQ$ cắt nhau tại trung điểm $I$ của mỗi đường.

b) Tương tự chứng minh trên ta cũng có tứ giác $RNSM$ cũng là hình bình hành do có

$\left\{ \begin{gathered}
RN//MS \hfill \\
RN = MS = \frac{1}{2}AD \hfill \\
\end{gathered} \right.$
suy ra $RS$ và $MN$ cũng cắt nhau tại trung điểm $I$ của $MN$.

Vậy ba đoạn $MN,PQ,RS$ cắt nhau tại trung điểm $I$ của mỗi đoạn.

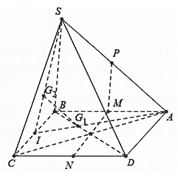
Câu 5. Cho hình chóp $S.ABCD$, có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD.

a) Chứng minh MN song song với các mặt phẳng $\left( {SBC} \right)$, $\left( {SAD} \right)$.

b) Gọi P là trung điểm của SA. Chứng minh SB, SC đều song song với $\left( {MNP} \right)$.

c) Gọi ${G_1}$, ${G_2}$ lần lượt là trọng tâm của các tam giác ABC, SBC. Chứng minh rằng: ${G_1}{G_2}//\left( {SAC} \right)$

Lời giải

a) Vì M, N là trung điểm của AB, CD nên $MN//A{\text{D}}//BC$

Ta có: $\left\{ \begin{gathered}
AD \in \left( {SAD} \right) \hfill \\
MN//AD \hfill \\
MN \notin \left( {SAD} \right) \hfill \\
\end{gathered} \right. \Rightarrow MN//\left( {SAD} \right)$

Tương tự, ta có: $\left\{ \begin{gathered}
BC \in \left( {SBC} \right) \hfill \\
MN//BC \hfill \\
MN \notin \left( {SBC} \right) \hfill \\
\end{gathered} \right. \Rightarrow MN//\left( {SBC} \right)$

b) Vì P là trung điểm SA nên $\left\{ \begin{gathered}
MP//SB \hfill \\
NP//SC \hfill \\
\end{gathered} \right.$

Ta có: $\left\{ \begin{gathered}
MP \in \left( {MNP} \right) \hfill \\
SB//MP \hfill \\
SB \notin \left( {MNP} \right) \hfill \\
\end{gathered} \right. \Rightarrow SB//\left( {MNP} \right)$

Tương tự chứng minh trên ta có: $\left\{ \begin{gathered}
NP \in \left( {MNP} \right) \hfill \\
SC//NP \hfill \\
SC \notin \left( {MNP} \right) \hfill \\
\end{gathered} \right. \Rightarrow SC//\left( {MNP} \right)$

c) Gọi I là trung điểm của BC $ \Rightarrow \left\{ \begin{gathered}
{G_1} \in AI \hfill \\
{G_2} \in BC \hfill \\
\end{gathered} \right.$ và $\frac{{I{G_1}}}{{IA}} = \frac{{I{G_2}}}{{IS}} = \frac{1}{3} \Rightarrow {G_1}{G_2}//SA \Rightarrow {G_1}{G_2}//\left( {SAC} \right)$.

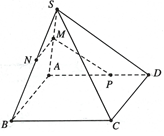
Câu 6. Cho hình chóp S.ABCD có ABCD là hình bình hành. Trên các cạnh SA, SB, AD lần lượt lấy M, N, P sao cho $\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{{PD}}{{AD}}$. Chứng minh:

a) MN song song với mặt phẳng $\left( {ABCD} \right)$.

b) SD song song với mặt phẳng $\left( {MNP} \right)$.

c) NP song song với mặt phẳng $\left( {SCD} \right)$.

Lời giải

a) Ta có: $\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} \Rightarrow MN//AB$ (định lý Talet đảo)

Suy ra $MN//\left( {ABCD} \right)$.

b) Tương tự $\frac{{SM}}{{SA}} = \frac{{PD}}{{AD}} \Rightarrow MP//SD$ (định lý Talet đảo)

Suy ra $SD//\left( {MNP} \right)$.

c) Ta có: $MP//SD$

Mặt khác $MN//AB \Rightarrow MN//CD$

Do đó $\left( {MNP} \right)//\left( {SCD} \right) \Rightarrow NP//\left( {SCD} \right)$.

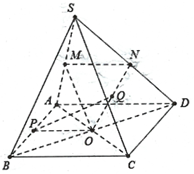
Câu 7: Cho hình chóp $S.ABCD$, có đáy là hình bình hành tâm $O$. Gọi $M,N$ lần lượt là trung điểm của $SA,SD$.

a) Chứng minh rằng $\left( {OMN} \right)//\left( {SBC} \right)$.

b) Gọi $P,Q$ lần lượt là trung điểm của $AB,ON$. Chứng minh $PQ//\left( {SBC} \right).$

Lời giải

a) Ta có $MO$ là đường trung bình trong tam giác $SAC \Rightarrow MO\parallel AC.$

Mặt khác $N$ và $O$ lần lượt là trung điểm của $SD$ và $BD$ nên $NO$ là đường trung bình trong $\Delta SBD \Rightarrow NO\parallel SB.$

Ta có: $\left\{ \begin{gathered}
MO\parallel SC \hfill \\
NO\parallel SB \hfill \\
MO \cap NO = O \hfill \\
SC \cap SB = S \hfill \\
\end{gathered} \right. \Rightarrow \left( {OMN} \right)\parallel \left( {SBC} \right).$

b) Do $P$ và $O$ lần lượt là trung điểm của $AB$ và $AC$ nên $OP\parallel AD\parallel BC \Rightarrow OP\parallel \left( {SBC} \right).$

Lại có $ON\parallel SB \Rightarrow OQ\parallel \left( {SBC} \right).$

Do vậy $\left( {OPQ} \right)\parallel \left( {SBC} \right) \Rightarrow PQ\parallel \left( {SBC} \right).$

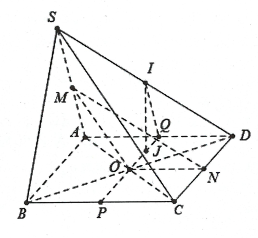
Câu 8: Cho hình chóp $S.ABCD$, có đáy là hình bình hành tâm $O$. Gọi $M,N$ lần lượt là trung điểm của $SA$ và $CD$.

a) Chứng minh rằng $\left( {OMN} \right)\parallel \left( {SBC} \right).$

b) Gọi $I$ là trung điểm của $SD,J$ là một điểm trên $\left( {ABCD} \right)$ và cách đều $AB,CD$. Chứng minh rằng $IJ\parallel \left( {SAB} \right)$.

Lời giải

a) Ta có $N$ và $O$ lần lượt là trung điểm của $CD$ và $AC$ nên $NO$ là đường trung bình trong $\Delta BCD \Rightarrow NO\parallel BC.$

Tương tự $MO$ là đường trung bình trong tam giác $SAC$ nên $MO\parallel SC.$

Lại có: $\left\{ \begin{gathered}
NO\parallel BC \hfill \\
MO\parallel SC \hfill \\
OM \cap ON = O \hfill \\
BC \cap SC = S \hfill \\
\end{gathered} \right. \Rightarrow \left( {OMN} \right)\parallel \left( {SBC} \right).$

b) Ta có $P$ và $Q$ lần lượt là trung điểm của $BC$ và $AD$ thì $PQ$ là đường thẳng cách đều $AB$ và $CD$ do vậy điểm $J \in PQ,$ Do $IQ$ là đường trung bình của $\Delta SAD$ nên $IQ\parallel SA.$

Ta có: $PQ\parallel \left( {SAB} \right);IQ\parallel \left( {SAB} \right) \Rightarrow \left( {IPQ} \right)\parallel \left( {SAB} \right)$

Mặt khác $IJ \subset \left( {IPQ} \right) \Rightarrow IJ\parallel \left( {SAB} \right).$