Trắc Nghiệm Bài 20 Hàm Số Mũ Và Hàm Số Lôgarit Giải Chi Tiết

Trắc nghiệm bài 20 Hàm số mũ và hàm số lôgarit được soạn dưới dạng file word và PDF gồm 16 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ MŨ VÀ LOGARIT

Phương pháp:

I. HÀM SỐ MŨ

1. Dạng: $y = f\left( x \right) = {a^x}$ với $\left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{a \ne 1}
\end{array}} \right.$.

Tập xác định: $D = \mathbb{R}$.

2. Dạng: $y = f\left( u \right) = {u^x}$ với $\left\{ {\begin{array}{*{20}{l}}
{u > 0} \\
{u \ne 1}
\end{array}} \right.$.

Tập xác định: $D = \mathbb{R}$.

II. HÀM SỐ LOGARIT

1. Dạng: $y = f\left( x \right) = lo{g_a}x$ với $\left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{a \ne 1}
\end{array}} \right.$.

Đặc biệt: $lo{g_a}x = lnx;lo{g_a}x = logx = {\text{lg}}x$.

Điều kiện xác định: $x > 0$.

2. Dạng: $y = f\left( u \right) = lo{g_a}u$ với $\left\{ {\begin{array}{*{20}{l}}
{u > 0} \\
{u \ne 1}
\end{array}} \right.$.

Đặc biệt: $lo{g_a}u = lnu;lo{g_a}u = logu = {\text{lg}}u$.

Điều kiện xác định: $u > 0$.

Câu 1. Tập xác định của hàm số $y = {9^x}$ là
A. $\mathbb{R}$.
B. $\left[ {0; + \infty } \right)$.
C. $\mathbb{R} \setminus \left\{ 0 \right\}$.
D. $\left( {0; + \infty } \right)$.

Lời giải

Chọn A.

Vì hàm số $y = {9^x}$ là hàm số mũ nên có tập xác định là tập $\mathbb{R}$.

Câu 2. Tập xác định của hàm số $y = {7^x}$ là:
A. $\mathbb{R} \setminus \left\{ 0 \right\}$.
B. $\left[ {0; + \infty } \right)$.
C. $\left( {0; + \infty } \right)$.
D. $\mathbb{R}$.

Lời giải

Chọn D.

Hàm số mũ $y = {a^x},0 < a \ne 1$ có tập xác định là $\mathbb{R}$.

Câu 3. Tập xác định của hàm số $y = lo{g_3}\left( {x – 4} \right)$ là
A. $\left( {5; + \infty } \right)$.
B. $\left( { – \infty ; + \infty } \right)$.
C. $\left( {4; + \infty } \right)$.
D. $\left( { – \infty ;4} \right)$.

Lời giải

Chọn C.

Điều kiện: $x – 4 > 0 \Leftrightarrow x > 4$.

Vậy tập xác định của hàm số đã cho là: $D = \left( {4; + \infty } \right)$.

Câu 4. Tập xác định của hàm số $y = lo{g_2}\left( {x – 1} \right)$ là
A. $\left( {2; + \infty } \right)$.
B. $\left( { – \infty ; + \infty } \right)$.
C. $\left( {1; + \infty } \right)$.
D. $\left( { – \infty ;1} \right)$.

Lời giải

Chọn C.

Hàm số xác định khi $x – 1 > 0 \Leftrightarrow x > 1$.

Tập xác định của hàm số là $D = \left( {1; + \infty } \right)$.

Câu 5. Tập xác định của hàm số $y = lo{g_{2024}}x$ là
A. $\left[ {0; + \infty } \right)$.
B. $\left( { – \infty ;0} \right)$.
C. $\left( {0; + \infty } \right)$.
D. $\left( { – \infty ; + \infty } \right)$.

Lời giải

Chọn C.

Điều kiện: $x > 0$.

Tập xác định: $D = \left( {0; + \infty } \right)$.

Câu 6. Có bao nhiêu số nguyên thuộc tập xác định của hàm số $y = log\left[ {\left( {6 – x} \right)\left( {x + 2} \right)} \right]$ ?
A. 7 .
B. 8 .
C. 9 .
D. Vô số.

Lời giải

Chọn A.

Điều kiện $\left( {6 – x} \right)\left( {x + 2} \right) > 0 \Leftrightarrow – 2 < x < 6 \Rightarrow D = \left( { – 2;6} \right)$.

Vậy có 7 số nguyên $x$ thuộc tập xác định của hàm số đã cho.

Câu 7. Tìm tập xác định của hàm số $y = lo{g_{2024}}\left( {3x – {x^2}} \right)$.
A. $D = \mathbb{R}$
B. $D = \left( {0; + \infty } \right)$
C. $D = \left( { – \infty ;0} \right) \cup \left( {3; + \infty } \right)$
D. $D = \left( {0;3} \right)$

Lời giải

Chọn D.

Hàm số xác định khi: $3x – {x^2} > 0 \Leftrightarrow x \in \left( {0;3} \right)$

Vậy $D = \left( {0;3} \right)$

Câu 8. Tìm tập xác định $D$ của hàm số $y = lo{g_2}\left( {{x^2} – 2x – 3} \right)$
A. $D = \left( { – \infty ; – 1\left] \cup \right[3; + \infty } \right)$
B. $D = \left[ { – 1;3} \right]$
C. $D = \left( { – \infty ; – 1} \right) \cup \left( {3; + \infty } \right)$
D. $D = \left( { – 1;3} \right)$

Lời giải

Chọn C.

$y = lo{g_2}\left( {{x^2} – 2x – 3} \right)$. Hàm số xác định khi ${x^2} – 2x – 3 > 0 \Leftrightarrow x < – 1$ hoặc $x > 3$

Vậy tập xác định: $D = \left( { – \infty ; – 1} \right) \cup \left( {3; + \infty } \right)$

Câu 9. Tìm tập xác định $D$ của hàm số $y = log\left( {{x^2} – 4x + 3} \right)$.
A. $D = \left( {1;3} \right)$
B. $D = \left( { – \infty ;1} \right) \cup \left( {3; + \infty } \right)$
C. $D = \left( { – \infty ;2 – \sqrt 2 } \right) \cup \left( {2 + \sqrt 2 ; + \infty } \right)$.
D. $D = \left( {2 – \sqrt 2 ;1} \right) \cup \left( {3;2 + \sqrt 2 } \right)$

Lời giải

Chọn B.

Điều kiện ${x^2} – 4x + 3 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x < 1} \\
{x > 3}
\end{array}} \right.$.

Câu 10. Tập xác định của $y = ln\left( { – {x^2} + 5x – 6} \right)$ là
A. $\left[ {2;3} \right]$
B. $\left( {2;3} \right)$
C. $\left( { – \infty ;2\left] \cup \right[3; + \infty } \right)$
D. $\left( { – \infty ;2} \right) \cup \left( {3; + \infty } \right)$

Lời giải

Chọn B.

Hàm số xác định khi và chỉ khi $ – {x^2} + 5x – 6 > 0 \Leftrightarrow 2 < x < 3$.

Vậy tập xác định của hàm số là $D = \left( {2;3} \right)$.

Câu 11. Tìm tập xác định của hàm số $y = lo{g_{\sqrt 5 }}\frac{1}{{6 – x}}$.
A. $\left( { – \infty ;6} \right)$
B. $\mathbb{R}$
C. $\left( {0; + \infty } \right)$
D. $\left( {6; + \infty } \right)$

Lời giải

Chọn A.

Điều kiện: $\frac{1}{{6 – x}} > 0 \Leftrightarrow 6 – x > 0 \Leftrightarrow x < 6$. Do đó tập xác định của hàm số là $\left( { – \infty ;6} \right)$.

Câu 12. Tìm tập xác định $D$ của hàm số $y = lo{g_5}\frac{{x – 3}}{{x + 2}}$.
A. $D = \left( { – \infty ; – 2} \right) \cup \left( {3; + \infty } \right)$
B. $D = \left( { – 2;3} \right)$
C. $D = \left( { – \infty ; – 2} \right) \cup \left[ {3; + \infty } \right)$
D. $D = \mathbb{R} \setminus \left\{ { – 2} \right\}$

Lời giải

Chọn A.

Tập xác định của là tập các số $x$ để $\frac{{x – 3}}{{x + 2}} > 0 \Leftrightarrow \left( {x – 3} \right)\left( {x + 2} \right) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x > 3} \\
{x < – 2}
\end{array}} \right.$

Suy ra $D = \left( { – \infty ; – 2} \right) \cup \left( {3; + \infty } \right)$.

Câu 13. Tìm tập xác định của hàm số: $y = {2^{\sqrt x }} + log\left( {3 – x} \right)$
A. $\left[ {0; + \infty } \right)$.
B. $\left( {0;3} \right)$.
C. $\left( { – \infty ;3} \right)$.
D. $\left[ {0;3} \right)$.

Lời giải

Chọn D.

Điều kiện xác định: $\left\{ {\begin{array}{*{20}{l}}
{x \geqslant 0} \\
{3 – x > 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \geqslant 0} \\
{x < 3}
\end{array} \Rightarrow D = \left[ {0;3} \right)} \right.} \right.$

Câu 14. Tập xác định của hàm số $y = {[ln\left( {x – 2} \right)]^\pi }$ là
A. $\mathbb{R}$.
B. $\left( {3; + \infty } \right)$.
C. $\left( {0; + \infty } \right)$.
D. $\left( {2; + \infty } \right)$.

Lời giải

Chọn B.

ĐKХĐ: $\left\{ {\begin{array}{*{20}{l}}
{ln\left( {x – 2} \right) > 0} \\
{x – 2 > 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 2 > 1} \\
{x – 2 > 0}
\end{array} \Leftrightarrow x – 2 > 1 \Leftrightarrow x > 3} \right.} \right.$.

TXĐ: $D = \left( {3; + \infty } \right)$.

Câu 15. Tìm tập xác định $D$ của hàm số $y = lo{g_{2024}}\left( {4 – {x^2}} \right) + {(2x – 3)^{ – 2024}}$.
A. $D = \left[ { – 2;\frac{3}{2}} \right) \cup \left( {\frac{3}{2};2} \right]$.
B. $D = \left( { – 2;\frac{3}{2}} \right) \cup \left( {\frac{3}{2};2} \right)$.
C. $D = \left( {\frac{3}{2};2} \right)$.
D. $D = \left( { – 2;2} \right)$.

Lời giải

Chọn B.

Điều kiện có nghĩa của hàm số là $\left\{ {\begin{array}{*{20}{l}}
{4 – {x^2} > 0} \\
{2x – 3 \ne 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{ – 2 < x < 2} \\
{x \ne \frac{3}{2}}
\end{array}} \right.} \right.$

Vậy tập xác định của hàm số là $D = \left( { – 2;\frac{3}{2}} \right) \cup \left( {\frac{3}{2};2} \right)$

Câu 16. Tìm tập xác định của hàm số $y = \sqrt {{{(x – 2)}^0}} + lo{g_2}\left( {9 – {x^2}} \right)$ là
A. $D = \left( {2;3} \right)$.
B. $D = \left( { – 3;3} \right) \setminus \left\{ 2 \right\}$.
C. $D = \left( {3; + \infty } \right)$.
D. $D = \left( { – 3;3} \right)$.

Lời giải

Chọn B.

• Điều kiện xác định: $\left\{ {\begin{array}{*{20}{l}}
{x – 2 \ne 0} \\
{9 – {x^2} > 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \ne 2} \\
{ – 3 < x < 3}
\end{array}} \right.} \right.$

• Vậy tập xác định của hàm số là: $D = \left( { – 3;3} \right) \setminus \left\{ 2 \right\}$.

DẠNG 2: TẬP XÁC ĐỊNH CỦA HÀM SỐ MŨ, LOGARIT CHỨA THAM SỐ

Câu 17. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = log\left( {{x^2} – 4x – m + 1} \right)$ có tập xác định là $\mathbb{R}$.
A. $m > – 4$.
B. $m < 0$.
C. $m < – 4$.
D. $m < – 3$.

Lời giải

Chọn D

Hàm số $y = log\left( {{x^2} – 4x – m + 1} \right)$ có tập xác định là $\mathbb{R}$ khi và chỉ khi ${x^2} – 4x – m + 1 > 0\forall x \in \mathbb{R}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta< 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 > 0} \\
{16 – 4\left( { – m + 1} \right) < 0}
\end{array} \Leftrightarrow m < – 3} \right.} \right.$

Câu 18. Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = lo{g_{2024}}\left( {{x^2} – 2mx + 4} \right)$ xác định với mọi $x \in \mathbb{R}$ ?
A. 2 .
B.3.
C. 4 .
D. 5 .

Lời giải

Chọn B.

Hàm số xác định $\forall x \in \mathbb{R} \Leftrightarrow {x^2} – 2mx + 4 > 0,\forall x \in \mathbb{R}$.

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta< 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 > 0} \\
{4{m^2} – 16 < 0}
\end{array} \Leftrightarrow – 2 < m < 2.} \right.} \right.$

Do $m \in \mathbb{Z}$ nên $m \in \left\{ { – 1;0;1} \right\}$.

Câu 19. Hàm số $y = ln\left( {{x^2} + mx + 1} \right)$ xác định với mọi giá trị của $x$ khi.
A. $\left[ {\begin{array}{*{20}{l}}
{m < – 2} \\
{m > 2}
\end{array}} \right.$.
B. $m > 2$.
C. $ – 2 < m < 2$.
D. $m < 2$.

Lời giải

Chọn C

Yêu cầu bài toán $ \Leftrightarrow {x^2} + mx + 1 > 0,\forall x \in \mathbb{R}$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta< 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 > 0} \\
{{m^2} – 4 < 0}
\end{array} \Leftrightarrow – 2 < m < 2} \right.} \right.$

Câu 20. Có bao nhiêu giá trị nguyên của tham số $m$ trên [-2024; 2024] để hàm số $y = ln\left( {{x^2} – 2x – m + 1} \right)$ có tập xác định là $\mathbb{R}$ ?
A. 4046
B. 2025
C. 2024
D. 4047

Lời giải

Chọn C

Hàm số $y = ln\left( {{x^2} – 2x – m + 1} \right)$ có tập xác định là $\mathbb{R}$ khi và chỉ khi:

${x^2} – 2x – m + 1 > 0\forall x \in \mathbb{R} \Leftrightarrow \Delta ‘ < 0 \Leftrightarrow 1 + m – 1 < 0 \Leftrightarrow m < 0$.

Kết hợp với điều kiện $m$ nguyên thuộc [-2024; 2024] ta có 2024 giá trị của $m$.

Câu 21. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = log\left( {{x^2} – 2mx + 4} \right)$ có tập xác định là $\mathbb{R}$ ?
A. 6
B. 5
C. 4
D. 3

Lời giải

Chọn D

$y = log\left( {{x^2} – 2mx + 4} \right)$

Điều kiện xác định của hàm số trên: ${x^2} – 2mx + 4 > 0$.

Để tập xác định của hàm số là $\mathbb{R}$ thì $\left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta ‘ < 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{1 > 0,\forall m} \\
{{m^2} – 4 < 0}
\end{array} \Leftrightarrow – 2 < m < 2} \right.} \right.$.

Kết hợp với điều kiện $m$ nguyên ta có 3 giá trị của $m$.

Câu 22. Có tất cả bao nhiêu giá trị nguyên của tham số $m$ nằm trong khoảng $\left( { – 2024;2024} \right)$ để hàm số $y = lo{g_2}\left[ {\left( {m + 2} \right){x^2} + 2\left( {m + 2} \right)x + m + 3} \right]$ có tập xác định $D = \mathbb{R}$.
A. 2027 .
B. 2025
C. 2026
D. 4052

Lời giải

Chọn C.

Hàm số xác định trên $\mathbb{R} \Leftrightarrow \left( {m + 2} \right){x^2} + 2\left( {m + 2} \right)x + m + 3 > 0,\forall x \in \mathbb{R}$

Trường hợp 1: $m + 2 = 0 \Leftrightarrow m = – 2$, ta có

$\left( * \right) \Leftrightarrow 1 > 0,\forall x \in \mathbb{R}$ (đúng), suy ra $m = – 2$ thỏa mãn. (1)

Truờng hợp 2: $m \ne – 2$.

$\left( * \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = m + 2 > 0} \\
{\Delta= 4{{(m + 2)}^2} – 4\left( {m + 2} \right)\left( {m + 3} \right) < 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > – 2} \\
{ – m – 2 < 0}
\end{array} \Leftrightarrow m > – 2} \right.} \right.$. (2)

Từ (1) và (2) suy ra $m \geqslant – 2$ thì hàm số có tập xác định $D = \mathbb{R}$.

Suy ra có 2026 giá trị nguyên của tham số $m$ nằm trong khoảng $\left( { – 2024;2024} \right)$ thỏa mãn.

Câu 23. Có bao nhiêu giá trị nguyên của tham số $m$ trên $\left( { – 100;2024} \right]$ để hàm số $y = lo{g_{2026}}\left( {mx – m + 2} \right)$ có tập xác định với mọi $x \in \mathbb{R}$ ?
A. 4042
B. 2023
C. 2025
D. 2024

Lời giải

Chọn C

Điều kiện: $mx – m + 2 > 0 \Leftrightarrow mx > m – 2$

• Trường hợp 1: $m = 0 \Rightarrow \left( 1 \right)$ trở thành $0 > – 1$ (luôn thỏa mãn).

• Trường hợp 2: $m > 0 \Rightarrow \left( 1 \right) \Leftrightarrow x > \frac{{m – 2}}{m} \Rightarrow $ Tập xác định của hàm số là $D = \left( {\frac{{m – 2}}{m}; + \infty } \right)$. Khi đó, yêu cầu bài toán trở thành $\frac{{m – 2}}{m} < 1 \Leftrightarrow m – 2 < m \Leftrightarrow – 2 < 0$ (luôn thỏa mãn).

• Trường hợp $3:m < 0 \Rightarrow \left( 1 \right) \Leftrightarrow x < \frac{{m – 2}}{m} \Rightarrow $ Tập xác định của hàm số là $D = \left( { – \infty ;\frac{{m – 2}}{m}} \right)$. Do đó không tồn tại $m$ thỏa mãn yêu cầu bài toán.

Vậy tất cả các giá trị cần tìm là $m \geqslant 0$.

Kết hợp với điều kiện $m$ nguyên thuộc (-100; 2024] ta có 2025 giá trị của $m$.

Câu 24. Số các giá trị nguyên của tham số $m$ để hàm số $y = log\left( {mx – m + 2} \right)$ xác định trên $\left[ {\frac{1}{2}; + \infty } \right)$ là
A. 4
B. 5
C. Vô số
D. 3

Lời giải

Chọn A

Điều kiện xác định: $mx – m + 2 > 0 \Leftrightarrow mx > m – 2$

Trường hợp 1. $m = 0$.

$\left( 1 \right) \Leftrightarrow 2 > 0$ (luôn đúng với $\forall x \in \left[ {\frac{1}{2}; + \infty } \right)$ ).

Trường hợp 2. $m > 0$.

$\left( 1 \right) \Leftrightarrow x > \frac{{m – 2}}{m}$

Để hàm số $y = log\left( {mx – m + 2} \right)$ xác định trên $\left[ {\frac{1}{2}; + \infty } \right)$ thì $\frac{{m – 2}}{m} < \frac{1}{2} \Leftrightarrow 0 < m < 4$.

Vì $m \in \mathbb{Z}$ nên $m \in \left\{ {1;2;3} \right\}$.

Trường họ̣p 3. $m < 0$.

(1) $ \Leftrightarrow x < \frac{{m – 2}}{m}$.

Suy ra tập xác định của hàm số $y = log\left( {mx – m + 2} \right)$ là $D = \left( { – \infty ;\frac{{m – 2}}{m}} \right)$.

Do đó $\left[ {\frac{1}{2}; + \infty } \right) \not\subset D$ suy ra không có giá trị $m < 0$ nào thỏa yêu cầu bài toán.

Từ 3 trường hợp trên ta được $m \in \left\{ {0;1;2;3} \right\}$.

Câu 25. Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đọ̣n $\left[ { – 1000;1000} \right]$ để hàm số $y = ln\left( { – {x^2} + mx + 2m + 1} \right)$ xác định với mọi $x \in \left( {1;2} \right)$ ?
A. 1001 .
B. 2000 .
C. 2001 .
D. 1000 .

Lời giải

Chọn D.

Hàm số xác định với mọi $x \in \left( {1;2} \right)$ khi $ – {x^2} + mx + 2m + 1 > 0,\forall x \in \left( {1;2} \right)$.

$ \Leftrightarrow f\left( x \right) = {x^2} – mx – 2m – 1 < 0,\forall x \in \left( {1;2} \right)$.

$ \Rightarrow f\left( x \right) = 0$ có 2 nghiệm thỏa mãn ${x_1} \leqslant 1 < 2 \leqslant {x_2}$.

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( 1 \right) \leqslant 0} \\
{f\left( 2 \right) \leqslant 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{ – 3m \leqslant 0} \\
{ – 4m + 3 \leqslant 0}
\end{array} \Leftrightarrow m \geqslant \frac{3}{4}} \right.} \right.$
$\left\{ {\begin{array}{*{20}{l}}
{m \in \mathbb{Z}} \\
{m \in \left[ { – 1000;1000} \right]}
\end{array} \Rightarrow m \in \left\{ {1,2,3, \ldots ,1000} \right\}} \right.$.

Kết luận: có 1000 giá trị của $m$ thỏa mãn bài toán.

Câu 26. Tìm tất cả giá trị thực của tham số $m$ để hàm số $y = lo{g_3}\left( {{x^2} – \left( {m + 1} \right)x + m} \right)$ xác định trên $\left( {1;4} \right)$
A. $ – \frac{3}{4} \leqslant m \leqslant 1$.
B. $m \leqslant 1$.
C. $m > 1$.
D. $m \leqslant – \frac{3}{4}$.

Lời giải

Chọn B.

Để hàm số $y = lo{g_3}\left( {{x^2} – \left( {m + 1} \right)x + m} \right)$ xác định trên $\left( {1;4} \right)$ thì

${x^2} – \left( {m + 1} \right)x + m > 0,\forall x \in \left( {1;4} \right) \Leftrightarrow \left( {x – 1} \right)\left( {x – m} \right) > 0,\forall x \in \left( {1;4} \right)$.

Do $1 < x < 4$ nên có các trường hợp sau

TH1: $m < 1 \Rightarrow \left[ {\begin{array}{*{20}{l}}
{x > 1} \\
{x < m < 1}
\end{array}} \right.$ vậy hàm số xác định trên $\left( {1;4} \right)$.

TH2: $m = 1$ thì ${(x – 1)^2} > 0 \Leftrightarrow x \ne 1$ vậy hàm số xác định trên $\left( {1;4} \right)$.

TH3: $m > 1 \Rightarrow \left[ {\begin{array}{*{20}{l}}
{x < 1} \\
{x > m > 1}
\end{array}} \right.$ như vậy hàm số không xác định trên $\left( {1;4} \right)$ (loại).

Kết luận: $m \leqslant 1$.

Câu 27. Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = \frac{3}{{\sqrt {x – m} }} + lo{g_5}\sqrt {2m + 1 – x} $ xác định trên khoảng $\left( {2;3} \right)$ ?
A.1.
B. 2 .
C. 3 .
D. 4 .

Lời giải

Chọn B.

Hàm số xác định $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – m > 0} \\
{2m + 1 – x > 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x > m} \\
{x < 2m + 1}
\end{array}} \right.} \right.$.

Xét các trường hợp sau:

+) Nếu $2m + 1 \leqslant m \Leftrightarrow m \leqslant – 1 \Rightarrow D = \phi $, suy ra không thỏa mãn.

+) Nếu $2m + 1 > m \Leftrightarrow m > – 1 \Rightarrow D = \left( {m;2m + 1} \right)$

Hàm số đã cho xác định trên khoảng (2;3) khi và chỉ khi

$\left( {2;3} \right) \subset D \Leftrightarrow m \leqslant 2 < 3 \leqslant 2m + 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m \leqslant 2} \\
{m \geqslant 1}
\end{array} \Leftrightarrow 1 \leqslant m \leqslant 2.} \right.$

Vì $m$ nguyên nên $m = \left\{ {1;2} \right\}$.

Câu 28. Có tất cả bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y = \frac{1}{{\sqrt {2m + 1 – x} }} + lo{g_3}\sqrt {x – m} $ xác định trên khoảng $\left( {2;3} \right)$ ?
A. 1 .
B. 2 .
C. 4
D. 3 .

Lời giải

Chọn B

Hàm số xác định $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2m + 1 – x > 0} \\
{x – m > 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x < 2m + 1} \\
{x > m}
\end{array} \Rightarrow D = \left( {m;2m + 1} \right)} \right.} \right.$.

Hàm số đã cho xác định trên khoảng $\left( {2;3} \right)$ nên $\left( {2;3} \right) \subset D = \left( {m;2m + 1} \right) \Leftrightarrow m \leqslant 2 < 3 \leqslant 2m + 1$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m \leqslant 2} \\
{2m + 1 \geqslant 3}
\end{array} \Leftrightarrow 1 \leqslant m \leqslant 2} \right.$.

Vì $m$ nguyên dương nên $m \in \left\{ {1;2} \right\}$.

Câu 29. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số

$y = \frac{1}{{\sqrt {7m – 5 – x} }} + lo{g_5}\left( {\sqrt {x – 3m + 1} } \right)$ xác định trên $\left( { – 1;3} \right).$

A. 0 .
B. 1 .
C. 2 .
D. 4 .

Lời giải

Chọn A.

Để hàm số xác định ta có .

$\left\{ {\begin{array}{*{20}{l}}
{x < 7m – 5} \\
{x > 3m – 1}
\end{array}} \right.$

TH1: của hàm số là $D = \emptyset $ (loại).

TH2: $3m – 1\left\langle {7m – 5 \Leftrightarrow m} \right\rangle 1 \Rightarrow $ TXĐ của hàm số là $D = \left( {3m – 1;7m – 5} \right)$.

Để hàm số xác định trên $\left( { – 1;3} \right)$ thì

$\left( { – 1;3} \right) \subset D \Leftrightarrow \left( { – 1;3} \right) \subset \left( {3m – 1;7m – 5} \right)$

$ \Leftrightarrow 3m – 1 \leqslant – 1 < 3 \leqslant 7m – 5 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m \leqslant 0} \\
{m \geqslant \frac{8}{7}}
\end{array}} \right.$ (Vô nghiệm)

Vậy không có giá trị nào của $m$ để hàm số xác định trên (-1;3).

DẠNG 3: ĐỒ THỊ CỦA HÀM SỐ MŨ VÀ LOGARIT

Phương pháp

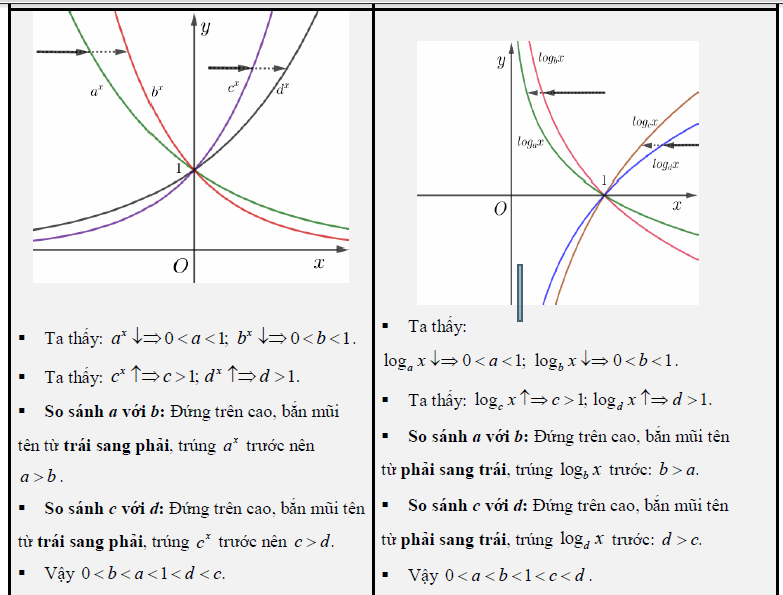
Câu 30. Cho $a,b,c$ là ba số dương khác 1 . Đồ thị các hàm số $y = lo{g_a}x,y = lo{g_b}x,y = lo{g_c}x$ được cho trong hình vẽ bên. Mệnh đề nào dưới đây là mệnh đề đúng?

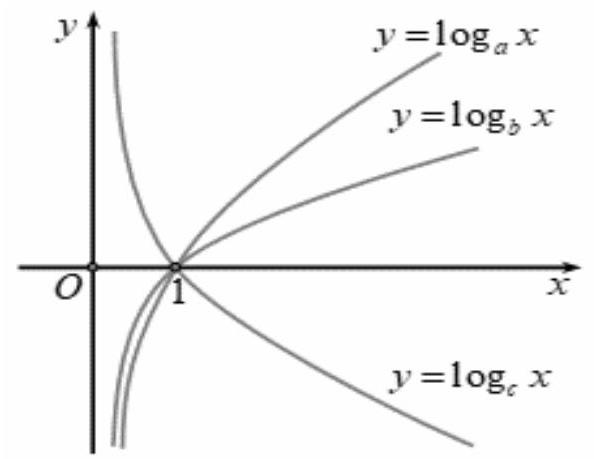
A. $a < b < c$.
B. $c < a < b$.
C. $c < b < a$.
D. $b < c < a$.

Lời giải

Chọn B.

• Đồ thị các hàm số $y = lo{g_a}x,y = lo{g_b}x,y = lo{g_c}x$ lần lượt đi qua các điểm $A\left( {a;1} \right),B\left( {b;1} \right)$, $C\left( {c;1} \right)$

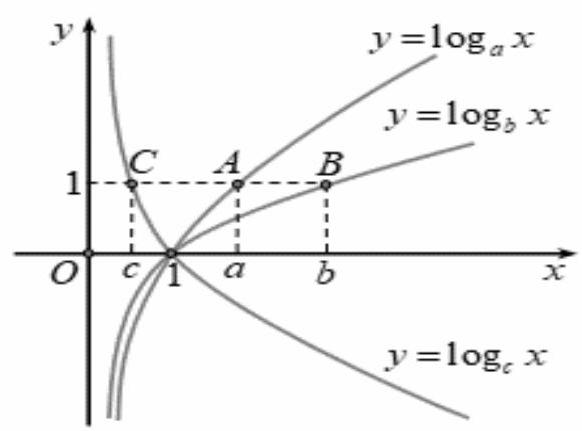
• Từ hình vẽ ta có: $c < a < b$.

Câu 31. Cho ba số thực dương $a,b,c$ khác 1 . Đồ thị các hàm số $y = {a^x},y = {b^x},y = {c^x}$ được cho trong hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?

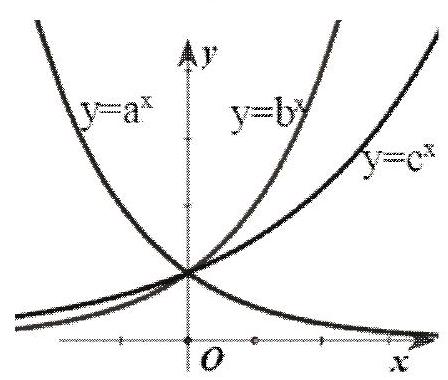
A. $1 < a < c < b$.
B. $a < 1 < c < b$.
C. $a < 1 < b < c$.
D. $1 < a < b < c$.

Lời giải

Chọn B.

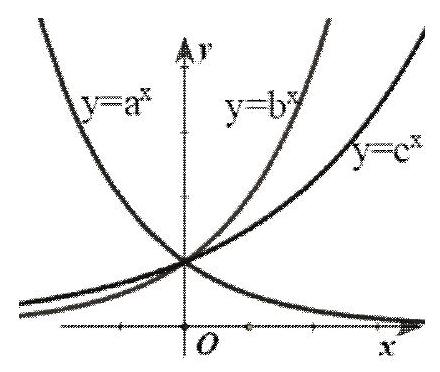
Đồ thị của hàm số $y = {a^x}$ có hướng đi xuống nên $a < 1$.

Đồ thị của các hàm số $y = {b^x}$ và $y = {c^x}$ có hướng đi lên nên $b > 1$ và $c > 1$. Hơn nữa đồ thị hàm số $y = {b^x}$ ở phía trên đồ thị hàm số $y = {c^x}$ nên $b > c$.

Vậy $a < 1 < c < b$.

Câu 32. Cho bốn hàm số $y = {(\sqrt 3 )^x}\left( 1 \right),y = {\left( {\frac{1}{{\sqrt 3 }}} \right)^x}\left( 2 \right),y = {4^x}\left( 3 \right),y = {\left( {\frac{1}{4}} \right)^x}$ (4) có đồ thị là 4 đường cong theo phía trên đồ thị, thứ tự từ trái qua phải là $\left( {{C_1}} \right),\left( {{C_2}} \right),\left( {{C_3}} \right),\left( {{C_4}} \right)$ như hình vẽ bên.

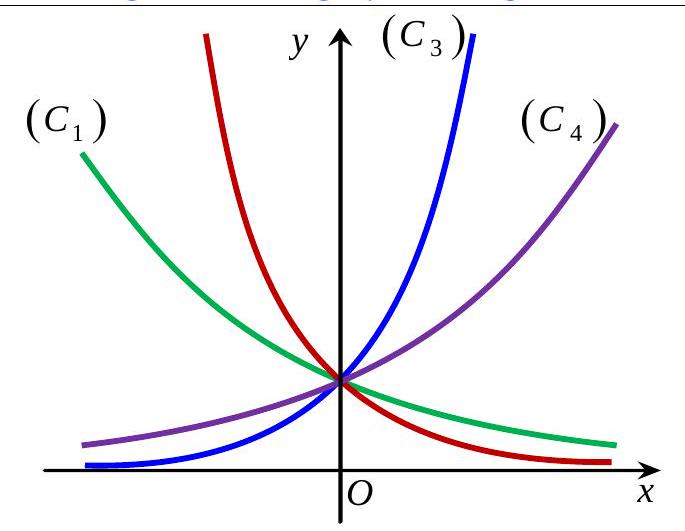
Tương ứng hàm số – đồ thị đúng là
A. $\left( 1 \right) – \left( {{C_2}} \right),\left( 2 \right) – \left( {{C_3}} \right),\left( 3 \right) – \left( {{C_4}} \right),\left( 4 \right) – \left( {{C_1}} \right)$.
B. $\left( 1 \right) – \left( {{C_1}} \right),\left( 2 \right) – \left( {{C_2}} \right),\left( 3 \right) – \left( {{C_3}} \right),\left( 4 \right) – \left( {{C_4}} \right)$.
C. $\left( 1 \right) – \left( {{C_4}} \right),\left( 2 \right) – \left( {{C_1}} \right),\left( 3 \right) – \left( {{C_3}} \right),\left( 4 \right) – \left( {{C_2}} \right)$.
D. $\left( 1 \right) – \left( {{C_1}} \right),\left( 2 \right) – \left( {{C_2}} \right),\left( 3 \right) – \left( {{C_3}} \right),\left( 4 \right) – \left( {{C_4}} \right)$.

Lời giải

Chọn C.

Ta có $y = {(\sqrt 3 )^x}$ và $y = {4^x}$ có cơ số lớn hơn 1 nên hàm đồng biến nên nhận đồ thị là $\left( {{C_3}} \right)$ hoặc $\left( {{C_4}} \right)$. Lấy $x = 2$ ta có ${(\sqrt 3 )^2} < {4^2}$ nên đồ thị $y = {4^x}$ là $\left( {{C_3}} \right)$ và đồ thị $y = {(\sqrt 3 )^x}$ là $\left( {{C_4}} \right)$.

Ta có đồ thị hàm số $y = {4^x}$ và $y = {\left( {\frac{1}{4}} \right)^x}$ đối xứng nhau qua $Oy$ nên đồ thị $y = {\left( {\frac{1}{4}} \right)^x}$ là $\left( {{C_2}} \right)$. Còn lại $\left( {{C_1}} \right)$ là đồ thị của $y = {\left( {\frac{1}{{\sqrt 3 }}} \right)^x}$.

Vậy (1) $ – \left( {{C_4}} \right),\left( 2 \right) – \left( {{C_1}} \right),\left( 3 \right) – \left( {{C_3}} \right),\left( 4 \right) – \left( {{C_2}} \right)$

Câu 33. Trong hình vẽ dưới đây có đồ thị của các hàm số $y = {a^x},y = {b^x},y = lo{g_c}x$.

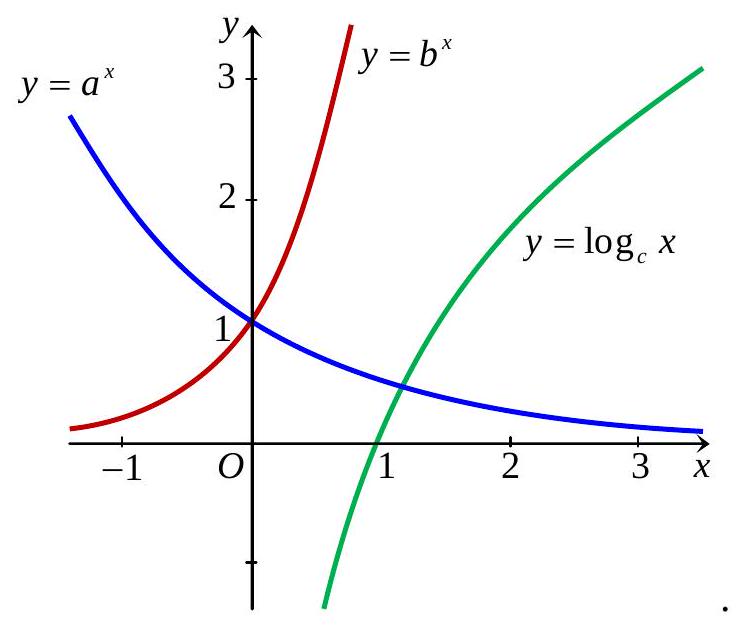
Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
A. $c < a < b$.
B. $a < c < b$.
C. $b < c < a$.
D. $a < b = c$.

Lời giải

Chọn B.

Từ đồ thị Ta thấy hàm số $y = {a^x}$ nghịch biến $ \Rightarrow 0 < a < 1$.

Hàm số $y = {b^x},y = lo{g_c}x$ đồng biến $ \Rightarrow b > 1,c > 1$

$ \Rightarrow a < b,a < c$ nên loại A, C

Nếu $b = c$ thì đồ thị hàm số $y = {b^x}$ và $y = lo{g_c}x$ phải đối xứng nhau qua đường phân giác góc phần tư thứ nhất $y = x$. Nhưng ta thấy đồ thị hàm số $y = lo{g_c}x$ cắt đường $y = x$ nên loại ${\mathbf{D}}$.

Câu 34. Cho hàm số $y = {a^x},y = {b^x}$ với $a,b$ là hai số thực dương khác 1 , lần lượt có đồ thị là $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ như hình bên. Mệnh đề nào dưới đây đúng?

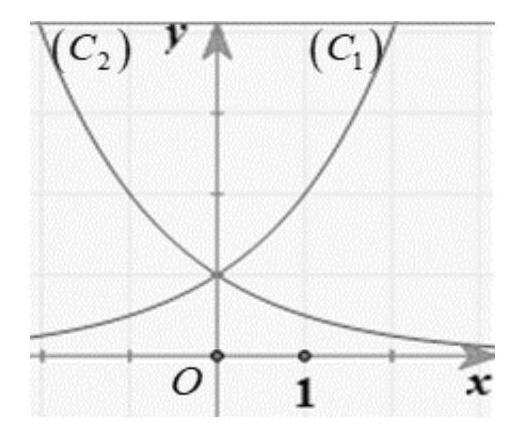
A. $0 < b < 1 < a$
B. $0 < a < b < 1$
C. $0 < b < a < 1$
D. $0 < a < 1 < b$

Lời giải

Chọn A.

Theo hình ta thấy hàm $y = {a^x}$ là hàm đồng biến nên $a > 1$, còn hàm $y = {b^x}$ là hàm nghịch biến nên $0 < b < 1$. Suy ra $0 < b < 1 < a$.

Câu 35. Cho ba số thực dương $a,b,c$ khác 1. Đồ thị các hàm số $y = {a^x},y = {b^x},y = {c^x}$ được cho trong hình vẽ bên

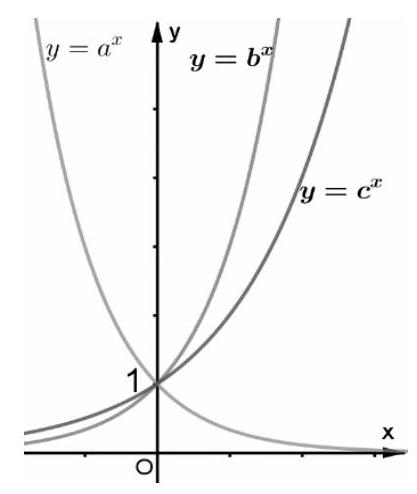
Mệnh đề nào dưới đây đúng?
A. $b < c < a$
B. $c < a < b$
C. $a < b < c$
D. $a < c < b$

Lời giải

Chọn D.

Đường thẳng $x = 1$ đồ thị các hàm số $y = {a^x},y = {b^x},y = {c^x}$ tại các điểm có tung độ lần lượt là $y = a,y = b,y = c$ như hình vẽ:

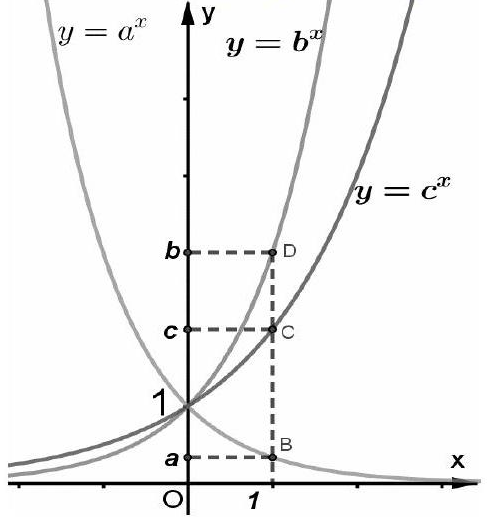
Từ đồ thị kết luận $a < c < b$

Câu 36. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

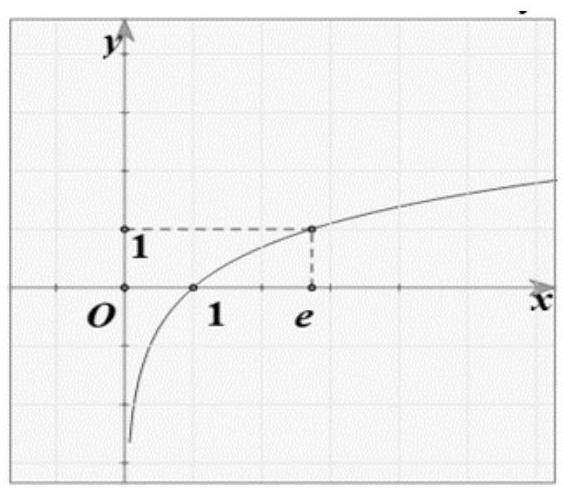
A. $y = – {e^x}$.
B. $y = \left| {lnx} \right|$.
C. $y = lnx$.
D. $y = {e^x}$.

Lời giải

Chọn C.

Đồ thị hàm số đi qua điểm $\left( {e;1} \right)$ và nằm cả trên và dưới trục hoành nên chỉ có hàm số $y = lnx$ thoả mãn.

Câu 37. Cho đồ thị hàm số $y = {a^x}$ và $y = lo{g_b}x$ như hình vẽ.

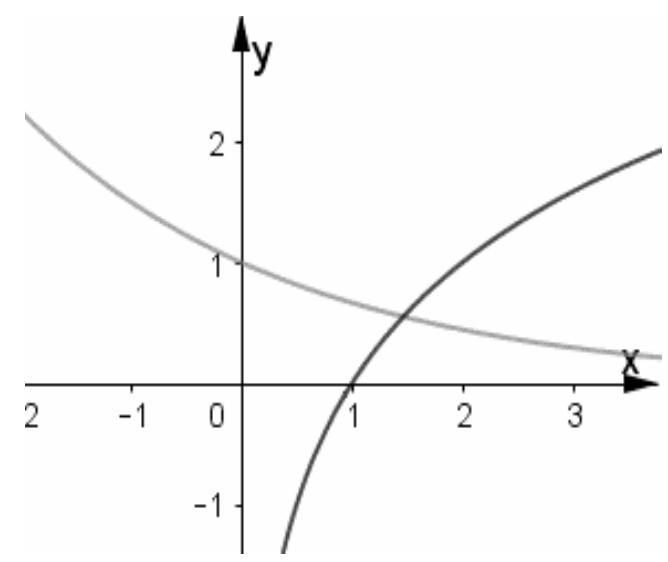
Khẳng định nào sau đây đúng?
A. $0 < a < \frac{1}{2} < b$.
B. $0 < a < 1 < b$.
C. $0 < b < 1 < a$.
D. $0 < a < 1,0 < b < \frac{1}{2}$.

Lời giải

Chọn B.

Xét hàm số $y = {a^x}$ đi qua $\left( {0;1} \right)$ suy ra đồ thị hàm số (1) là đồ thị của hàm nghịch biến nên $0 < a < 1$. Xét đồ thị hàm số $y = lo{g_b}x$ đi qua $\left( {1;0} \right)$ suy ra đồ thị của hàm số (2) là đồ thị của hàm đồng biến suy ra $b > 1$.

Vậy $0 < a < 1 < b$.

Câu 38. Hàm số nào sau đây có đồ thị như hình bên?

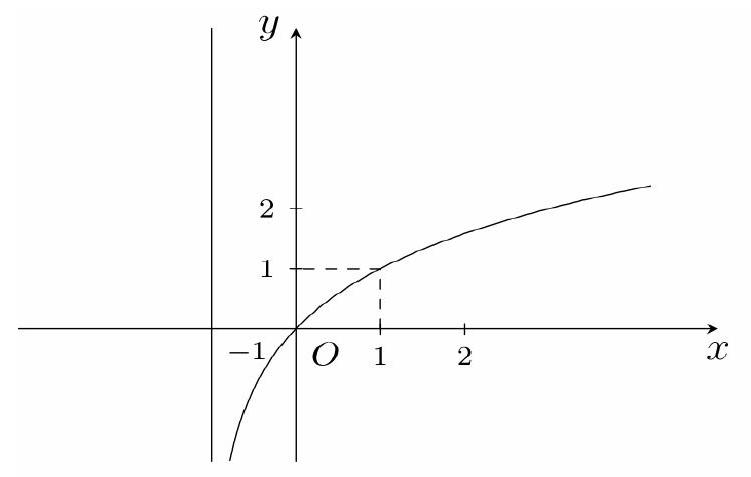
A. $y = lo{g_3}x$.
B. $y = lo{g_2}x + 1$.
C. $y = lo{g_2}\left( {x + 1} \right)$.
D. $y = lo{g_3}\left( {x + 1} \right)$

Lời giải

Chọn C.

Đồ thị hàm số đi qua điểm $\left( {0;0} \right)$ nên loại đáp án $A$ và

Đồ thị hàm số đi qua điểm $\left( {1;1} \right)$ nên loại $D$.

Vậy đáp án $c$ thỏa mãn.

Câu 39. Cho đồ thị hàm số $y = {a^x}$ và $y = lo{g_b}x$ như hình vẽ. Trong các khẳng định sau, đâu là khẳng định đúng

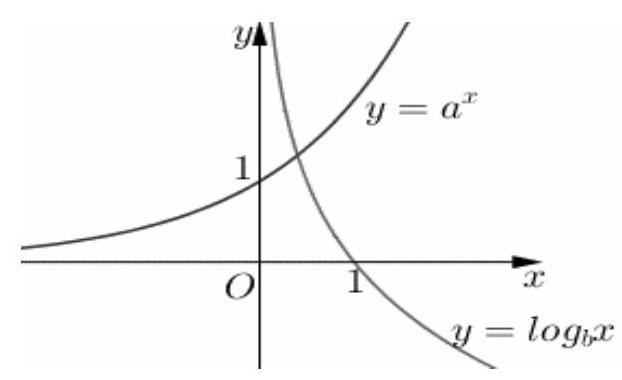
A. $0 < a < 1,0 < b < 1$.
B. $a > 1,b > 1$.
C. $0 < b < 1 < a$.
D. $0 < a < 1 < b$.

Lời giải

Chọn C.

Dựa vào đồ thị ta thấy khi $x \to – \infty \Rightarrow y \to 0$ do đó đồ thị hàm số $y = {a^x}$ có $a > 1$. Nên ta loại đáp án $a$ và. D.

Ở đồ thị hàm số $y = lo{g_b}x \Leftrightarrow x = {b^y}$ ta thấy khi $x \to + \infty \Rightarrow y \to – \infty $ do đó ta có $0 < b < 1$.

Câu 40. Hình vẽ bên thể hiện đồ thị của ba trong bốn hàm số $y = {6^x},y = {8^x},y = \frac{1}{{{5^x}}}$ và $y = \frac{1}{{{{\sqrt 7 }^x}}}$.

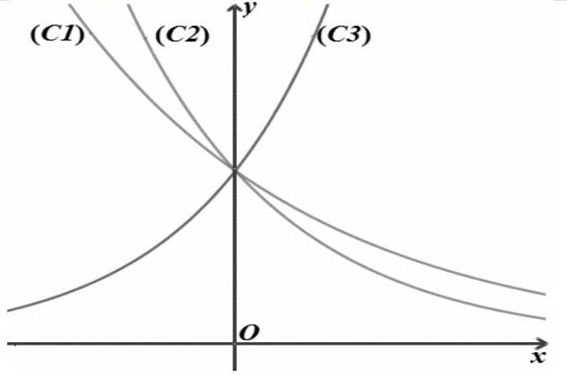
Hỏi $\left( {{c_2}} \right)$ là đồ thị hàm số nào?
A. $y = {6^x}$.
B. $y = \frac{1}{{{{\sqrt 7 }^x}}}$.
C. $y = \frac{1}{{{5^x}}}$.
D. $y = {8^x}$

Lời giải

Chọn B.

Hàm số có đồ thị $\left( {{c_2}} \right)$ là hàm số nghịch biến, do đó loại đáp án A, D.

Cho $x = 1$ suy ra $\frac{1}{{\sqrt 7 }} > \frac{1}{5}$

Do đó đồ thị hàm số $\left( {{c_2}} \right)$ là $y = \frac{1}{{{5^x}}}$.

Câu 41. Hàm số $y = lo{g_a}x$ và $y = lo{g_b}x$ có đồ thị như hình bên.

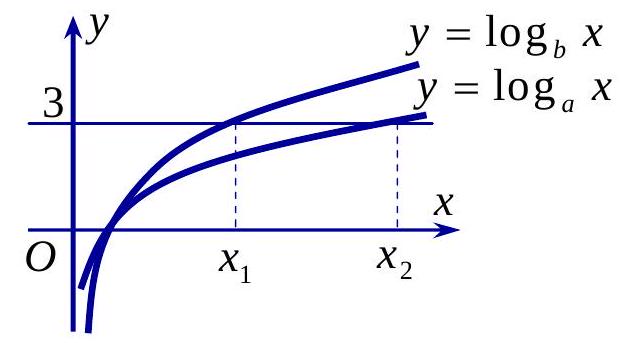
Đường thẳng $y = 3$ cắt hai đồ thị tại các điểm có hoành độ là ${x_1};{x_2}$. Biết rằng ${x_1} = 2{x_2}$. Giá trị của $\frac{a}{b}$ bằng
A. $\frac{1}{3}$.
B. $\sqrt 3 $.
C. 2 .
D. $\sqrt[3]{2}$.

Lời giải

Chọn D.

Xét phương trình hoành độ giao điểm $lo{g_a}x = 3 \Leftrightarrow {x_1} = {a^3}$, và $lo{g_b}x = 3 \Leftrightarrow {x_2} = {b^3}$.

Ta có ${x_1} = 2{x_2} \Leftrightarrow {a^3} = 2{b^3} \Leftrightarrow {\left( {\frac{a}{b}} \right)^3} = 2 \Leftrightarrow \frac{a}{b} = \sqrt[3]{2}$.

Câu 42. Trong hình dưới đây, điểm $B$ là trung điểm của đoạn thẳng $AC$. Khẳng định nào sau đây là đúng?

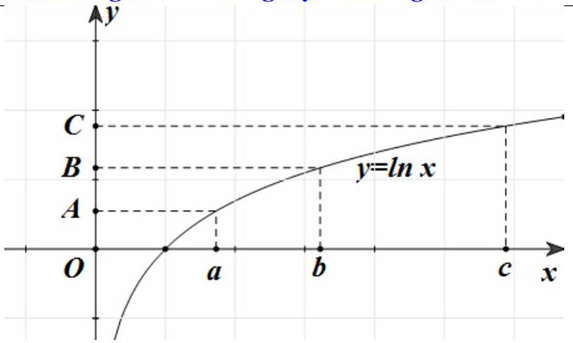
A. $a + c = 2b$.
B. $ac = {b^2}$.
C. $ac = 2{b^2}$.
D. $ac = b$.

Lời giải

Chọn B.

Ta có $A\left( {0;lna} \right),B\left( {0;lnb} \right),C\left( {0;lnc} \right)$ và $B$ là trung điểm của $AC$ nên $lna + lnc = 2lnb \Leftrightarrow ln\left( {ac} \right) = ln{b^2} \Leftrightarrow ac = {b^2}$.

Vậy $ac = {b^2}$.

Câu 43. Trong hình vẽ bên các đường cong $\left( {{C_1}} \right):y = {a^x},\left( {{C_2}} \right):y = {b^x},\left( {{C_3}} \right):y = {c^x}$ và đường thẳng $y = 4;y = 8$ tạo thành hình vuông $MNPQ$ có cạnh bằng 4 .

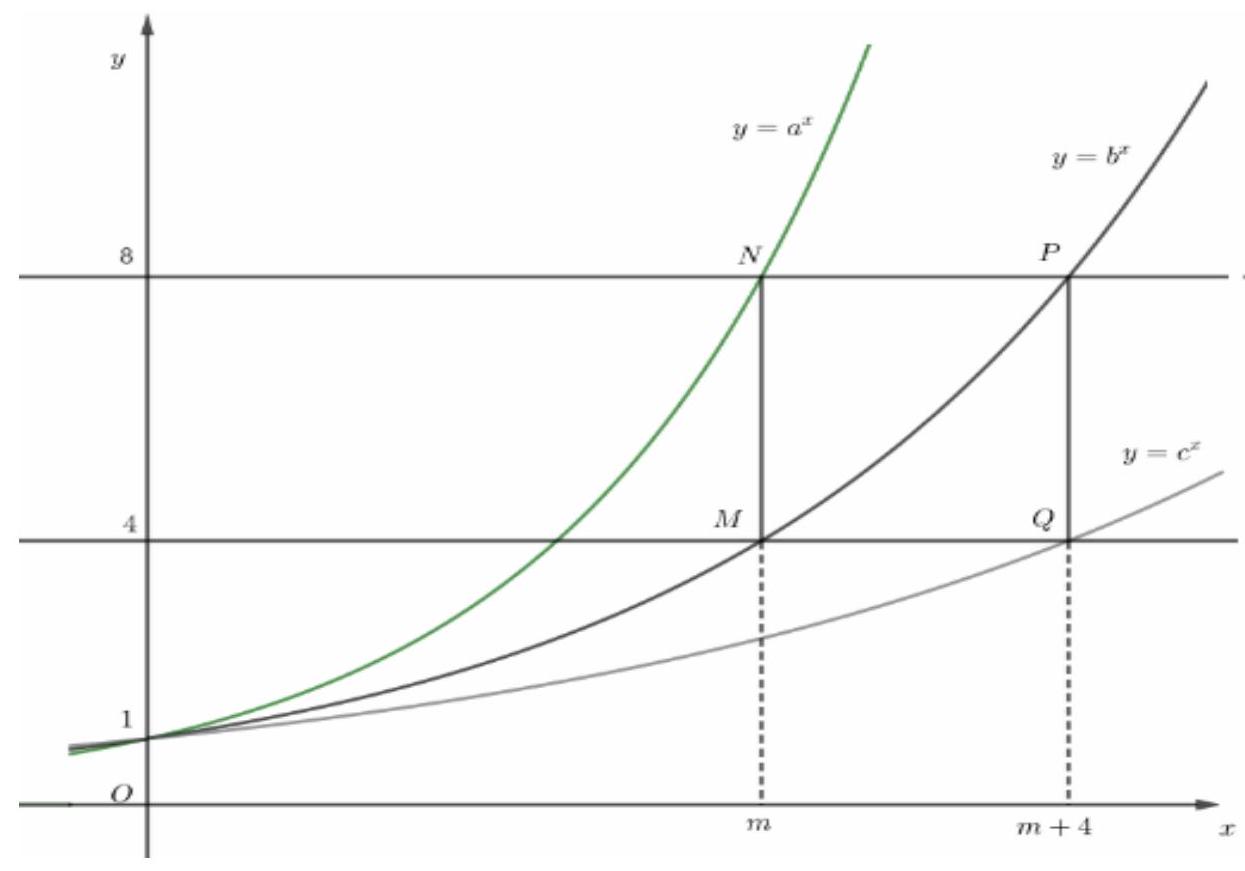
Biết rằng $abc = {2^{\frac{x}{y}}}$ với $x;y \in {\mathbb{Z}^ + }$và $\frac{x}{y}$ tối giản, giá trị của $x + y$ bằng
A. 34 .
B. 5 .
C. 43 .
D. 19 .

Lời giải

Chọn C.

Giả sử hoành độ điểm $M$ là $m$, ta suy ra $M\left( {m;4} \right);N\left( {m;8} \right);P\left( {m + 4;8} \right)$; Q $\left( {m + 4;4} \right)$.

Từ giả thiết ta có $M,P$ thuộc đường cong $y = {b^x}$ nên $\left\{ {\begin{array}{*{20}{l}}
{{b^m} = 4} \\
{{b^{m + 4}} = 8}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{b^m} = 4} \\
{{b^4} = 2}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m = 8} \\
{b = {2^{\frac{1}{4}}}}
\end{array}} \right.} \right.} \right.$ $N,Q$ lần lượt thuộc đường cong $y = {a^x};y = {c^x}$ nên $\left\{ {\begin{array}{*{20}{l}}
{{a^8} = 8} \\
{{c^{12}} = 4}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{a^8} = {2^3}} \\
{{c^{12}} = {2^2}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = {2^{\frac{3}{8}}}} \\
{c = {2^{\frac{1}{6}}}}
\end{array}} \right.} \right.} \right.$.

Khi đó $abc = {2^{\frac{3}{8}}} \cdot {2^{\frac{1}{4}}} \cdot {2^{\frac{1}{6}}} = {2^{\frac{3}{8} + \frac{1}{4} + \frac{1}{6}}} = {2^{\frac{{19}}{{24}}}}$.Vậy $x = 19;y = 24 \Rightarrow x + y = 43$.

Câu 44. Cho số thực dương $a$ khác 1 . Biết rằng bất kỳ đường thẳng nào song song với trục $Ox$ mà cắt các đường $y = {4^x},y = {a^x}$, trục tung lần lượt tại $M,N$ và $A$ thì $AN = 2AM$ ( hình vẽ bên). Giá trị của $a$ bằng

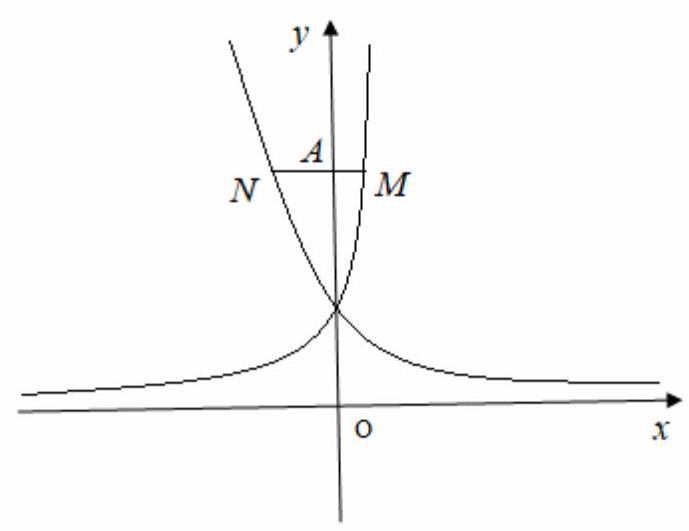
A. $\frac{1}{3}$.
B. $\frac{{\sqrt 2 }}{2}$.
C. $\frac{1}{4}$.
D. $\frac{1}{2}$.

Lời giải

Chọn D.

Dựa vào ĐTHS ta thấy hàm số $y = {a^x}$ nghịch biến nên $0 < a < \frac{1}{2}$.

Mọi đường thẳng $y = m(\,m > 0)$ đều cắt các đường $y = {4^x},y = {a^x}$, trục tung lần lượt tại $M\left( {lo{g_4}m;m} \right),N\left( {lo{g_a}m;m} \right)$ và $A = \left( {0;m} \right)$, theo bài

$AN = 2AM \Leftrightarrow \left| {lo{g_a}m} \right| = 2\left| {lo{g_4}m} \right| \Leftrightarrow \left| {lo{g_a}m} \right| = \left| {lo{g_2}m} \right|$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{lo{g_a}m = lo{g_2}m} \\
{lo{g_a}m = – lo{g_2}m}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{lo{g_m}a = lo{g_m}2} \\
{lo{g_m}a = lo{g_m}\frac{1}{2}}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{a = 2} \\
{a = \frac{1}{2}}
\end{array}} \right.} \right.} \right.$

Vậy $a = \frac{1}{2}$.

Câu 45. Cho các hàm số $y = lo{g_a}x$ và $y = lo{g_b}x$ có đồ thị như hình vẽ bên. Đường thẳng $x = 5$ cắt trục hoành, đồ thị hàm số $y = lo{g_a}x$ và $y = lo{g_b}x$ lần lượt tại $A,B$ và $C$. Biết rằng $CB = 2AB$. Mệnh đề nào sau đây là đúng?

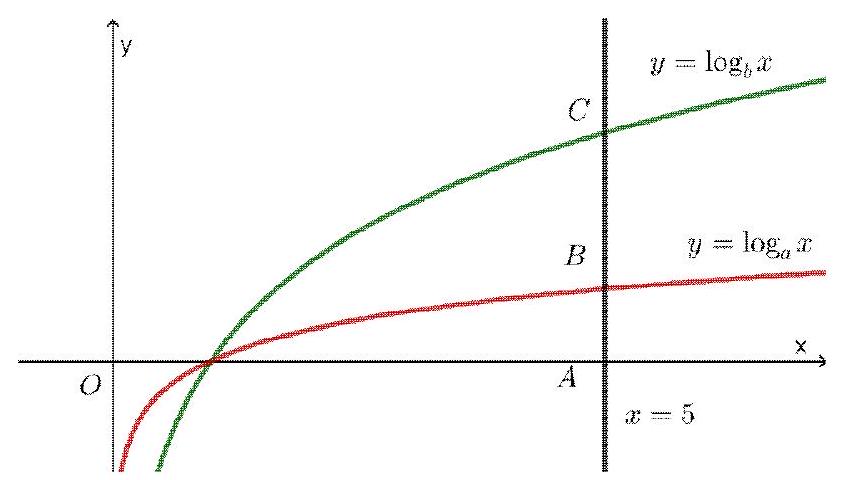
A. $a = 5b$.
B. $a = {b^2}$.
C. $a = {b^3}$.
D. ${a^3} = b$.

Lời giải

Chọn C.

Dễ thấy $A\left( {5;0} \right),B\left( {5;lo{g_a}5} \right),C\left( {5;lo{g_b}5} \right)$ và $lo{g_b}5 > lo{g_a}5 > 0$.

Do $CB = 2AB$ nên ta có $lo{g_b}5 – lo{g_a}5 = 2\left( {lo{g_a}5 – 0} \right)$.

$ \Leftrightarrow lo{g_b}5 = 3lo{g_a}5$

$ \Leftrightarrow \frac{1}{{lo{g_5}b}} = \frac{3}{{lo{g_5}a}}$

$ \Leftrightarrow lo{g_5}a = 3lo{g_5}b$

$ \Leftrightarrow lo{g_5}a = lo{g_5}{b^3}$

$ \Leftrightarrow a = {b^3}$.

Câu 46. Cho hàm số $y = {2^x}$ và $y = {2^{x – 2}}$ có đồ thị lần lượt là $\left( {{C_1}} \right),\left( {{C_2}} \right)$ như hình vẽ. Gọi $A$ là điểm thuộc $\left( {{C_1}} \right),B,C$ là các điểm thuộc $\left( {{C_2}} \right)$ sao cho tam giác $\vartriangle ABC$ là tam giác đều và $AB$ song song với $Ox$. Khi đó tọa độ điểm $C$ là $\left( {p;q} \right)$, giá trị của biểu thức ${2^p} + q$ bằng?

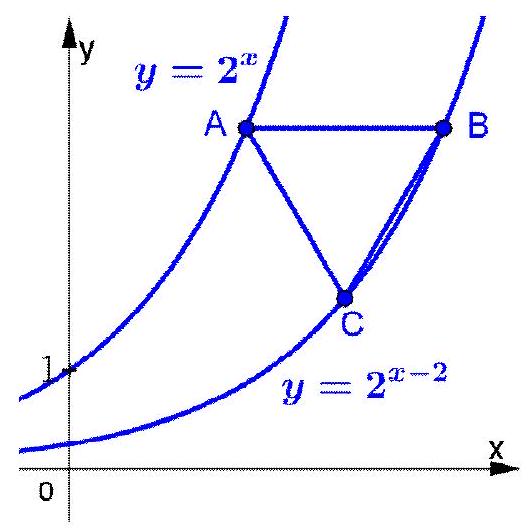
A. $5\sqrt 3 $.
B. $4\sqrt 3 $.
C. $6\sqrt 3 $.
D. $10\sqrt 3 $.

Lời giải

Chọn A.

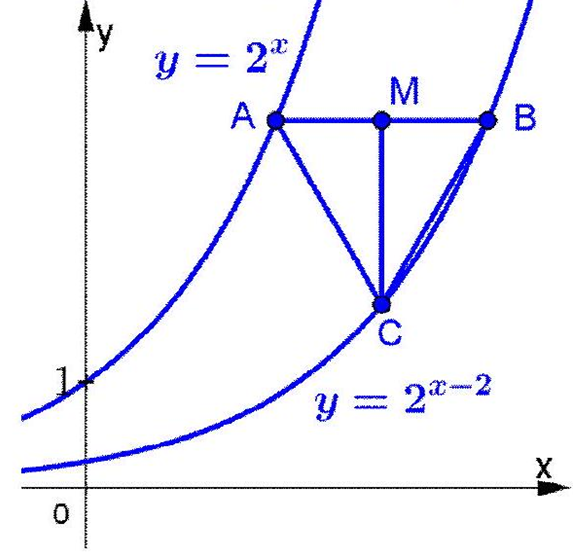
Gọi $A\left( {a;{2^a}} \right)$ và $B\left( {a + 2;{2^a}} \right)$. Khi đó trung điểm của $AB$ là $M\left( {a + 1;{2^a}} \right)$.

Ta có: $AB = 2$, do đó $CM = \sqrt 3 $. Vì $CM//Oy$ nên $C\left( {a + 1;{2^a} – \sqrt 3 } \right) \in \left( {{C_2}} \right)$. Khi đó ta có:

${2^{a – 1}} = {2^a} – \sqrt 3 \Leftrightarrow {2^a} = 2\sqrt 3 \Leftrightarrow a = 1 + lo{g_2}\sqrt 3 $.

Khi đó: $C\left( {2 + lo{g_2}\sqrt 3 ;\sqrt 3 } \right)$ hay ${2^p} + q = 5\sqrt 3 $.

Câu 47. Cho hai hàm số $y = {2^x},y = lo{g_2}x$ có đồ thị như hình vẽ. Đường thẳng $\Delta $ cắt trục tung, đồ thị hàm số $y = {2^x}$, đồ thị hàm số $y = lo{g_2}x$ và trục hoành lần lượt tại $A,B,C,D$ thỏa mãn $AB = BC = CD$. Hỏi có bao nhiêu đường thẳng $\Delta $ như thế ?

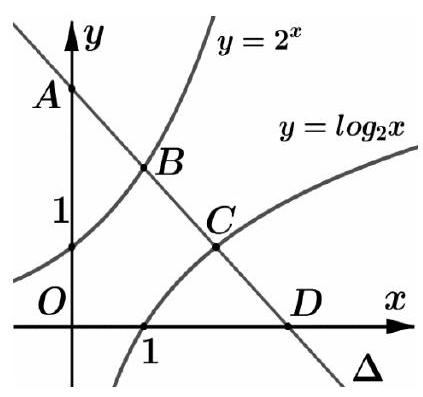
A. 1 .
B. 2 .
C. 3 .
D. Vô số.

Lời giải

Chọn B.

Gọi $\left\{ {\begin{array}{*{20}{l}}
{B\left( {b;{2^b}} \right) \in y = {2^x}} \\
{C\left( {c;lo{g_2}c} \right) \in y = lo{g_2}x}
\end{array}} \right.$$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{A\left( {2b – c;{2^{b + 1}} – lo{g_2}c} \right)} \\
{D\left( {2c – b;2lo{g_2}c – {2^b}} \right)}
\end{array}} \right.$

Vì $\left\{ {\begin{array}{*{20}{l}}
{A \in Oy} \\
{D \in Ox}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{2b – c = 0} \\
{2lo{g_2}c – {2^b} = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{c = 2b} \\
{lo{g_2}c = {2^{b – 1}}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{c = 2b} \\
{c = {2^{{2^{b – 1}}}}}
\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}
{b = 1,c = 2} \\
{b = 2,c = 4}
\end{array}} \right.} \right.} \right.} \right.} \right.$.

Vậy có hai bộ điểm $A,B,C,D$ thỏa yêu cầu bài toán. Hay có hai đường thẳng $\Delta$ như thế

Câu 48. Gọi $B$ và $C$ lần lượt là các điểm thuộc đồ thị hàm số $y = {2^x}$ và $y = lo{g_2}x$ sao cho tam giác $OBC$ đều. Giả sử điểm $B$ có hoành độ là $a$ khi đó tỉ số $\frac{{{2^x}}}{a}$ bằng

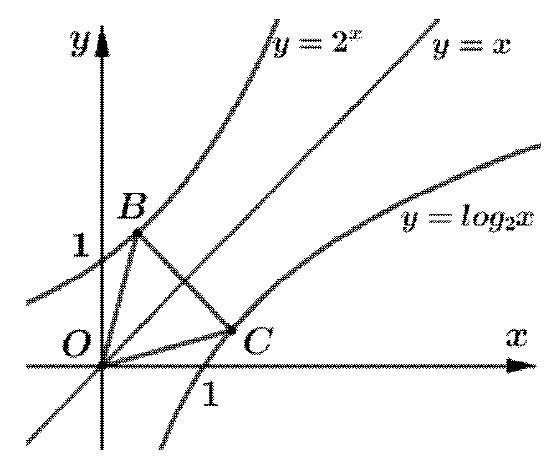
A. $2 – \sqrt 3 $.
B. $2 + \sqrt 3 $.
C. $2 – \sqrt 2 $.
D. $2 + \sqrt 2 $.

Lời giải

Chọn B.

Đồ thị hai hàm số $y = {2^x}$ và $y = lo{g_2}x$ đối xứng qua đường thẳng $y = x$ và theo yêu cầu bài toán là tam giác $OBC$ đều nên suy ra $B\left( {a;{2^a}} \right),C\left( {{2^a};a} \right)$ (theo đề điểm $B$ có hoành độ là $a$ ).

Tam giác $OBC$ đều $ \to OB = BC \Leftrightarrow O{B^2} = B{C^2} \Leftrightarrow {2^{2a}} – 4a \cdot {2^a} + {a^2} = 0$. Đấy là phương trình đẳng cấp và tìm được $\frac{{{2^x}}}{a} = 2 \pm \sqrt 3 $. Vì $B$ là điểm nằm trên đồ thị hàm số $y = {2^x}$ suy ra ${2^a} > a$ nên suy ra $\frac{{{2^x}}}{a} = 2 + \sqrt 3 $.

Câu 49. Gọi $A$ và $B$ là các điểm lần lượt nằm trên các đồ thị hàm số $y = lo{g_{\sqrt 2 }}x$ và $y = lo{g_{\frac{1}{2}}}x$ sao cho điểm $M\left( {2,0} \right)$ là trung điểm của đoạn thẳng $AB$. Diện tích tam giác $OAB$ là bao nhiêu biết rằng $O$ là gốc tọa độ?

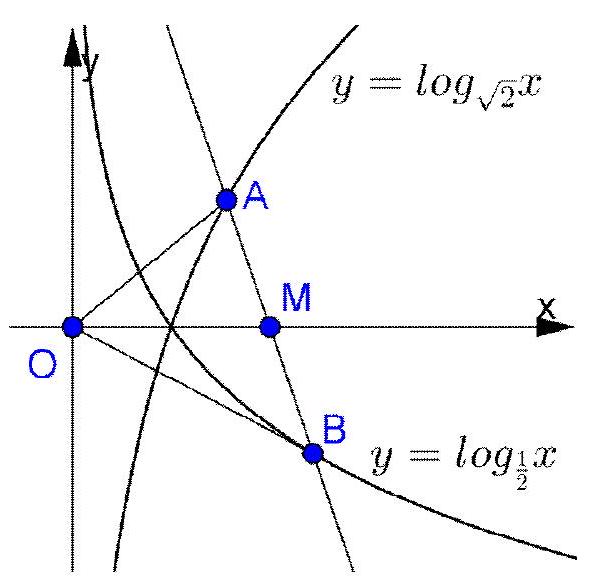
A. $S = 8lo{g_2}\left( {\frac{{\sqrt {17} – 1}}{2}} \right)$
B. $S = 4lo{g_2}\left( {\frac{{\sqrt {17} – 1}}{2}} \right)$
C. $S = 8lo{g_2}\left( {\frac{{\sqrt {17} + 1}}{2}} \right)$
D. $S = 4lo{g_2}\left( {\frac{{\sqrt {17} + 1}}{2}} \right)$

Lời giải

Chọn B.

Gọi tọa độ các điểm $A\left( {a,2lo{g_2}a} \right),B\left( {b, – lo{g_2}b} \right)$.

Vì $M\left( {2,0} \right)$ là trung điểm của đoạn thẳng $AB$ nên:

$\left\{ {\begin{array}{*{20}{l}}
{a + b = 4} \\
{2lo{g_2}a = lo{g_2}b}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{b = 4 – a} \\
{b = {a^2}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{b = 4 – a} \\
{{a^2} + a – 4 = 0}
\end{array} \Leftrightarrow a = \frac{{\sqrt {17} – 1}}{2}} \right.} \right.} \right.$

Vì $\left\{ {\begin{array}{*{20}{l}}
{a + b = 4} \\
{2lo{g_2}a = lo{g_2}b}
\end{array}} \right.$ nên $ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {OA} \left( {a,2lo{g_2}a} \right)} \\
{\overrightarrow {OB} \left( {4 – a, – 2lo{g_2}a} \right)}
\end{array}} \right.$

$ \Rightarrow S = \frac{{\left| {\left( {4 – a} \right)\left( {2lo{g_2}a} \right) – a\left( { – 2lo{g_2}a} \right)} \right|}}{2} = 4lo{g_2}\frac{{\sqrt {17} – 1}}{2}$

Câu 50. Với $a > 1$. Biết trên đồ thị của ba hàm số $y = lo{g_a}x,y = 2lo{g_a}x,y = 3lo{g_a}x$ lần lượt có 3 điểm $A,B,C$ sao cho tam giác $ABC$ vuông cân tại $B,AB$ song song với trục hoành và có diện tích bằng 18. Giá trị của $a$ bằng

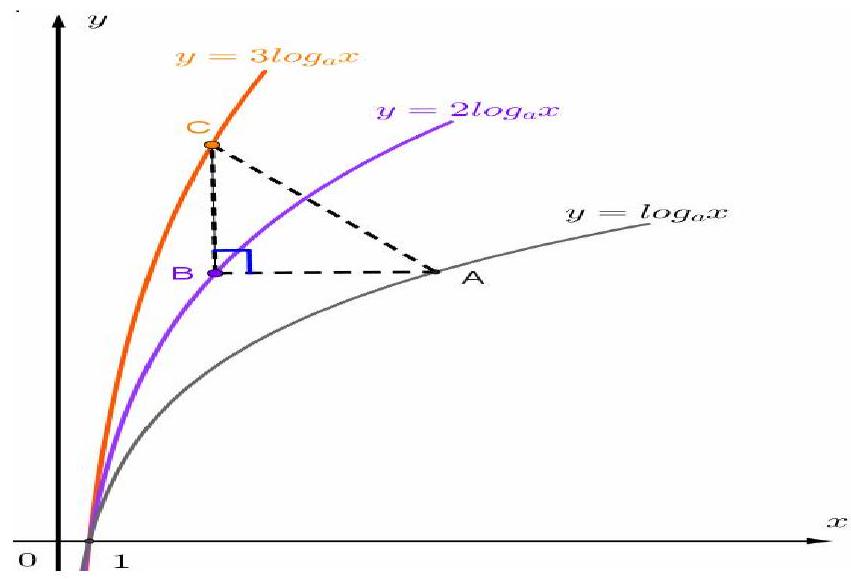
A. $\sqrt[6]{6}$.
B. $\sqrt[6]{3}$.
C. $\sqrt[3]{3}$.
D. $\sqrt[3]{6}$.

Lời giải

Chọn B.

Giả sử $B = \left( {m;2lo{g_a}m} \right)$ thì $A = \left( {{m^2};2lo{g_a}m} \right),C = \left( {m;3lo{g_a}m} \right),m > 0$.

Ta có $AB = \left| {{m^2} – m} \right|,BC = \left| {lo{g_a}m} \right|$.

Vì $AB = BC,{{\text{S}}_{\vartriangle ABC}} = 18$ nên $\frac{1}{2}AB \cdot BC = 18 \Rightarrow AB = BC = 6$.

$\left| {{m^2} – m} \right| = 6 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{m^2} – m – 6 = 0} \\
{{m^2} – m + 6 = 0\left( {VN} \right)}
\end{array};m > 0 \Rightarrow m = 3} \right.$.

$\left| {lo{g_a}m} \right| = 6 \Leftrightarrow \left| {lo{g_a}3} \right| = 6 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{lo{g_a}3 = 6} \\
{lo{g_a}3 = – 6 < 0}
\end{array},a > 1 \Rightarrow {a^6} = 3 \Leftrightarrow a = \sqrt[6]{3}} \right.$.

Câu 51. Cho ba hàm số $y = lo{g_a}x;y = lo{g_b}x;y = lo{g_c}x$ có đồ thị biểu diễn như hình vẽ. Biết rằng $5MA = 4MB = 3MC$. Giá trị nhỏ nhất của biểu thức $T = {a^6} + 3{b^{10}} + {c^{10}}$ bằng

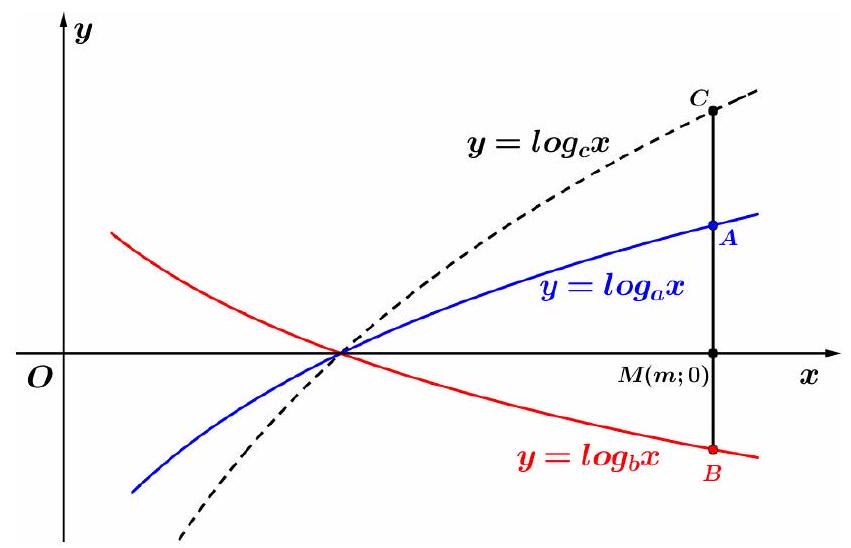
A. $2\sqrt[8]{{243}}$.
B. $\frac{7}{{\sqrt[7]{{16}}}}$.
C. $\frac{7}{{\sqrt[8]{{16}}}}$.
D. $4\sqrt[3]{{60}}$.

Lời giải

Chọn B.

Ta có: $c > a > 1 > b > 0$. Tiếp theo, ta có:

$\left\{ {\begin{array}{*{20}{l}}
{5MA = 3MC = 5lo{g_a}m = 3lo{g_c}m} \\
{5MA = 4MB = 5lo{g_a}m = 4lo{g_b}m}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{5}{{lo{g_m}a}} = \frac{3}{{lo{g_m}c}}} \\
{\frac{5}{{lo{g_m}a}} = \frac{4}{{lo{g_m}b}}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3lo{g_m}a = 5lo{g_m}c} \\
{4lo{g_m}a = 5lo{g_m}b}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{a^3} = {c^5}} \\
{{a^4} = {b^5}}
\end{array}} \right.} \right.} \right.$

Suy ra $T = {a^6} + 3{b^{10}} + {c^{10}} = {a^6} + \frac{3}{{{a^8}}} + {a^6} = 2{a^6} + \frac{3}{{{a^8}}} = \frac{{{a^6}}}{2} + \frac{{{a^6}}}{2} + \frac{{{a^6}}}{2} + \frac{{{a^6}}}{2} + \frac{1}{{{a^8}}} + \frac{1}{{{a^8}}} + \frac{1}{{{a^8}}}$

Theo Cosi, ta có: $T = \frac{{{a^6}}}{2} + \frac{{{a^6}}}{2} + \frac{{{a^6}}}{2} + \frac{{{a^6}}}{2} + \frac{1}{{{a^8}}} + \frac{1}{{{a^8}}} + \frac{1}{{{a^8}}} \geqslant 7\sqrt[7]{{\frac{{{a^6}}}{2} \cdot \frac{{{a^6}}}{2} \cdot \frac{{{a^6}}}{2} \cdot \frac{{{a^6}}}{2} \cdot \frac{1}{{{a^8}}} \cdot \frac{1}{{{a^8}}} \cdot \frac{1}{{{a^8}}}}} = \frac{7}{{\sqrt[7]{{16}}}}$

Nên suy ra ${T_{{\text{min}}}} = \frac{7}{{\sqrt[7]{{16}}}}$ khi và chỉ khi $\frac{{{a^6}}}{2} = \frac{1}{{{a^8}}} \Leftrightarrow a = \sqrt[{14}]{2} > 1$

Câu 52. Cho các số thực $a,b$ sao cho $0 < a,b \ne 1$, biết rằng đồ thị các hàm số $y = {a^x}$ và $y = lo{g_b}x$ cắt nhau tại điểm $M\left( {\sqrt {2018} ;\sqrt[5]{{{{2019}^{ – 1}}}}} \right)$. Mệnh đề nào dưới đây đúng?
A. $a > 1,b > 1$
B. $a > 1,0 < b < 1$
C. $0 < a < 1,b > 1$
D. $0 < a < 1,0 < b < 1$

Lời giải

Chọn C.

$M\left( {\sqrt {2018} ;\sqrt[5]{{{{2019}^{ – 1}}}}} \right)$ thuộc đồ thị hàm số $y = {a^x}$ nên ta có:

${a^{\sqrt {2018} }} = \sqrt[5]{{{{2019}^{ – 1}}}} = \frac{1}{{\sqrt[5]{{2019}}}} < 1 = {a^0} \Rightarrow 0 < a < 1$

$M\left( {\sqrt {2018} ;\sqrt[5]{{{{2019}^{ – 1}}}}} \right)$ thuộc đồ thị hàm số $y = lo{g_b}x$ nên ta có: $lo{g_b}\sqrt {2018} = \sqrt[5]{{{{2019}^{ – 1}}}} \Rightarrow {b^{\frac{1}{{\sqrt[5]{{2019}}}}}} = \sqrt {2018} > 1 = {b^0} \Rightarrow b > 1$

Vậy $0 < a < 1,b > 1$.

Câu 53. Đồ thị hàm số $y = f\left( x \right)$ đối xứng với đồ thị hàm số $y = {a^x}(a > 0,a \ne 1)$ qua điểm $I\left( {1;1} \right)$. Giá trị của biểu thức $f\left( {2 + lo{g_a}\frac{1}{{2018}}} \right)$ bằng
A. 2016 .
B. -2016 .
C. 2020 .
D. -2020 .

Lời giải

Chọn B.

Gọi $\left( C \right)$ là đồ thị hàm số $y = {a^x};\left( {{C_1}} \right)$ là đồ thị hàm số $y = f\left( x \right)$.

$M\left( {2 + lo{g_a}\frac{1}{{2018}};{y_M}} \right) \in \left( {{C_1}} \right) \Leftrightarrow {y_M} = f\left( {2 + lo{g_a}\frac{1}{{2018}}} \right)$.

Gọi $N$ đối xứng với $M$ qua $I\left( {1;1} \right) \Rightarrow N\left( { – lo{g_a}\frac{1}{{2018}};2 – {y_M}} \right)$.

Do đồ thị $\left( {{C_1}} \right)$ đối xứng $\left( C \right)$ qua $I\left( {1;1} \right)$ nên $N\left( { – lo{g_a}\frac{1}{{2018}};2 – {y_M}} \right) \in \left( C \right)$.

$N \in \left( C \right) \Leftrightarrow 2 – {y_M} = {a^{ – lo{g_a}\frac{1}{{2018}}}} \Leftrightarrow 2 – {y_M} = {a^{lo{g_a}2018}} \Leftrightarrow 2 – {y_M} = 2018 \Leftrightarrow {y_M} = – 2016$.

Vậy $f\left( {2 + lo{g_a}\frac{1}{{2018}}} \right) = – 2016$.

Câu 54. Đồ thị hàm số $y = f\left( x \right)$ đối xứng với đồ thị hàm số $y = lo{g_a}x,(0 < a \ne 1)$ qua điểm $I\left( {2;1} \right)$. Giá trị của biểu thức $f\left( {4 – {a^{2019}}} \right)$ bằng
A. 2023 .
B. -2023 .
C. 2017 .
D. -2017 .

Lời giải

Chọn D.

Lấy điểm $A\left( {4 – {a^{2019}};f\left( {4 – {a^{2019}}} \right)} \right)$ thuộc đồ thị của hàm số $y = f\left( x \right)$ và điểm $B\left( {x;lo{g_a}x} \right)$ thuộc đồ thị của hàm số $y = lo{g_a}x$.

Hai điểm $A$ và $B$ đối xứng nhau qua điểm $I$ khi và chỉ khi $\left\{ {\begin{array}{*{20}{l}}
{4 – {a^{2019}} + x = 2.2} \\
{f\left( {4 – {a^{2019}}} \right) + lo{g_a}x = 2.1}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = {a^{2019}}} \\
{f\left( {4 – {a^{2019}}} \right) + lo{g_a}{a^{2019}} = 2}
\end{array} \Rightarrow f\left( {4 – {a^{2019}}} \right) = – 2017} \right.} \right.$.